Algebra
Az algebra (arabul: الجبر, átírva "al-jabr", jelentése "a széttört részek újraegyesítése") a matematika (az Egyesült Államokban gyakran matematikának, az Egyesült Királyságban pedig matematikának vagy számmisztikának nevezik) egy része. Változókat használ egy még nem ismert érték ábrázolására. Ha egyenlőségjelet (=) használnak, akkor ezt egyenletnek nevezik. Egy nagyon egyszerű, változót használó egyenlet a következő: 2 + 3 = x. Ebben a példában x = 5, vagy azt is mondhatjuk, hogy "x egyenlő öt". Ezt hívják x megoldásának.
Az egyenletek mellett vannak egyenlőtlenségek is (kisebb és nagyobb, mint). Az egyenletek egy speciális típusát függvénynek nevezzük. Ezt gyakran használják grafikonok készítésénél, mert mindig egy bemenetet alakít át egy kimenetté.
Az algebra használható valós problémák megoldására, mert az algebra szabályai a valós életben is működnek, és a számok felhasználhatók valós dolgok értékeinek ábrázolására. A fizika, a mérnöki tudományok és a számítógépes programozás olyan területek, amelyek folyamatosan használják az algebrát. A földmérésben, az építőiparban és az üzleti életben, különösen a könyvelésben is hasznos az algebra ismerete.
Az algebrát művelő emberek a számok és a számokkal végzett matematikai műveletek szabályait használják. A legegyszerűbbek az összeadás, kivonás, szorzás és osztás. A fejlettebb műveletek az exponensekkel kapcsolatosak, kezdve a négyzetekkel és a négyzetgyökkel.
Az algebrát először egyenletek és egyenlőtlenségek megoldására használták. Két példa erre a lineáris egyenletek (egy egyenes egyenlete, y=mx+b) és a kvadratikus egyenletek, amelyekben a változókat négyzetre szorozzák (megszorozzák önmagukkal, például: 2*2, 3*3 vagy x*x).
Történelem
Az algebra korai formáit a babilóniaiak és a görög geométerek, mint például Alexandriai Héró, fejlesztették ki. Az "algebra" szó azonban az arab Al-Jabr ("öntés") szó latin formája, és az Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah ("Esszé az öntés és az egyenlet kiszámításáról") című matematikai könyvből származik, amelyet a 9. században írt egy perzsa matematikus, Muhammad ibn Mūsā al-Khwārizmī, aki az üzbegisztáni Khwarizmban született muszlim volt. Az iraki Bagdadban lévő al-Ma'moun alatt virágzott Kr. u. 813-833 között, és Kr. u. 840 körül halt meg. A könyv a 12. században került Európába és fordították le latinra. A könyv ekkor kapta az "Algebra" nevet. (A matematikus nevének végződését, al-Khwarizmi, egy latinul könnyebben kimondható szóra változtatták, és így lett az angol algoritmus szó).
Példák
Íme egy egyszerű példa egy algebrai feladatra:
Sue-nak 12 cukorkája van, Ann-nek pedig 24 cukorkája. Úgy döntenek, hogy osztoznak, így ugyanannyi cukorkájuk lesz. Hány cukorkát kapnak mindketten?
A következő lépésekkel oldhatja meg a problémát:
- Ahhoz, hogy ugyanannyi cukorkája legyen, Ann-nek oda kell adnia néhányat Sue-nak. Legyen x a cukorkák száma, amit Ann Sue-nak ad.
- Sue cukorkáinak plusz x-nek meg kell egyeznie Ann cukorkáival mínusz x. Ez a következőképpen írható le: 12 + x = 24 - x
- Vonjuk ki 12-t az egyenlet mindkét oldalából. Így kapjuk: x = 12 - x. (Ami az egyenlőségjel egyik oldalán történik, annak a másik oldalon is meg kell történnie, hogy az egyenlet továbbra is igaz legyen. Tehát ebben az esetben, amikor mindkét oldalról kivontuk a 12-t, egy középső lépést kaptunk: 12 + x - 12 = 24 - x - 12. Miután az ember megbarátkozott ezzel, a középső lépést nem írjuk le).
- Adjuk hozzá az x-et az egyenlet mindkét oldalához. Így kapjuk: 2x = 12
- Osszuk el az egyenlet mindkét oldalát 2-vel, így x = 6 lesz. A válasz hat. Ha Ann 6 cukorkát ad Sue-nak, akkor ugyanannyi cukorkájuk lesz.
- Ennek ellenőrzéséhez tegyük vissza a 6-ot az eredeti egyenletbe, ahol x volt: 12 + 6 = 24 - 6.
- Ez 18=18, ami igaz. Mindegyiküknek 18 cukorkája van.
Gyakorlással az algebra akkor is használható, ha olyan problémával találjuk szembe magunkat, amelyet túl nehéz más módon megoldani. Az olyan problémák, mint egy autópálya építése, egy mobiltelefon tervezése vagy egy betegség gyógymódjának megtalálása, mind algebrát igényelnek.
Írás algebra
Mint a matematika legtöbb területén, a z hozzáadását y-hoz (vagy y plusz z) y + z-ként írjuk. A z kivonását y-ból (vagy y mínusz z) y - z-ként írjuk. y osztását z-vel (vagy y-t z felett: y z {\displaystyle y \over z} ) 
y ÷ z-ként vagy y/z-ként írjuk. y/z az általánosan használt.
Az algebrában y és z (vagy y szorozva z-vel) szorzása 4 módon írható: y × z, y * z, y-z, vagy csak yz. Az "×" szorzási jelet általában nem használják, mert túlságosan hasonlít az x betűre, amelyet gyakran használnak változóként. Nagyobb kifejezések szorzásakor zárójeleket is használhatunk: y (z+1).
Amikor egy számot és egy betűt szorzunk össze az algebrában, a számot a betű elé írjuk: 5 × y = 5y. Ha a szám 1, akkor az 1-et nem írjuk, mert bármely szám 1-szerese az a szám (1 × y = y), így nincs rá szükség.
Mellékesen jegyezzük meg, hogy az algebrában nem kell az x vagy y betűket használni. A változók csak szimbólumok, amelyek valamilyen ismeretlen számot vagy értéket jelentenek, így bármilyen változót használhatsz. x és y azonban a leggyakoribbak.
Függvények és grafikonok
Az algebra fontos része a függvények tanulmányozása, mivel a függvények gyakran megjelennek az egyenletekben, amelyeket meg akarunk oldani. A függvény olyan, mint egy gép, amelybe egy számot (vagy számokat) be tudsz tenni, és egy bizonyos számot (vagy számokat) kapsz ki. A függvények használatakor a grafikonok hatékony eszközök lehetnek az egyenletek megoldásainak tanulmányozásában.
A grafikon egy olyan kép, amely a változók összes olyan értékét mutatja, amelyek az egyenletet vagy egyenlőtlenséget igazzá teszik. Általában ez könnyen elkészíthető, ha csak egy vagy két változó van. A grafikon gyakran egy egyenes, és ha a vonal nem kanyarodik vagy nem megy egyenesen fel-le, akkor az alapképlettel írható le: y = mx + b. A b változó a grafikon y metszéspontja (ahol a vonal keresztezi a függőleges tengelyt), m pedig a vonal meredeksége vagy meredeksége. Ez a képlet a grafikon koordinátáira vonatkozik, ahol az egyenes minden egyes pontját (x, y) írjuk.
Néhány matematikai feladatban, például egy egyenes egyenletében egynél több változó is lehet (ebben az esetben x és y). Az egyenes pontjainak megtalálásához az egyik változót megváltoztatjuk. A megváltoztatott változót "független" változónak nevezzük. Ezután a matematikai számítással egy számot kapunk. Az így kapott számot "függő" változónak nevezzük. A legtöbbször a független változót x-nek, a függő változót pedig y-nak írjuk, például az y = 3x + 1-ben. Ezt gyakran grafikonra helyezik, egy x tengelyt (balra és jobbra haladva) és egy y tengelyt (felfelé és lefelé haladva) használva. Függvény formájában is felírható: f(x) = 3x + 1. Tehát ebben a példában x helyére 5-t tehetünk, és y = 16-ot kapunk. Ha 2-t írnánk be x-nek, akkor y=7-et kapnánk. Ha pedig 0-t írnánk x-nek, akkor y=1-et kapnánk. Tehát a jobb oldali grafikonon látható módon a (5,16), (2,7) és (0,1) pontokon keresztül egy egyenes haladna.
Ha x hatványa 1, akkor egyenes. Ha négyzete vagy más hatványa van, akkor görbe lesz. Ha egyenlőtlenséget használ (< vagy > ), akkor általában a grafikon egy része árnyékolva van, vagy az egyenes felett vagy alatt.
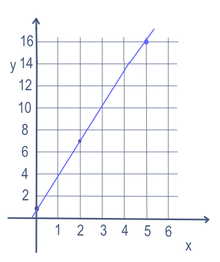
Az y=3x+1 egyenlet lineáris egyenlete
Az algebra szabályai
Az algebrában van néhány szabály, amely az egyenletek további megértéséhez használható. Ezeket az algebra szabályainak nevezzük. Bár ezek a szabályok értelmetlennek vagy nyilvánvalónak tűnhetnek, bölcs dolog megérteni, hogy ezek a tulajdonságok nem érvényesek a matematika minden ágában. Ezért hasznos lesz tudni, hogy ezek az axiomatikus szabályok hogyan vannak deklarálva, mielőtt magától értetődőnek vennénk őket. Mielőtt rátérnénk a szabályokra, gondolkodjunk el két meghatározáson, amelyeket megadunk.
- Ellentétes - a {\displaystyle a} ellentéte
- a {\displaystyle -a} 
. - Reciprok - a {\displaystyle a} reciproka 1 a {\displaystyle {\frac {\frac {1}{a}}}
.
Szabályok
Az összeadás kommutatív tulajdonsága
A "kommutatív" azt jelenti, hogy egy függvénynek ugyanaz az eredménye, ha a számokat felcseréljük. Más szóval, az egyenletben szereplő tagok sorrendje nem számít. Ha két tag operátora összeadás, akkor az "összeadás kommutatív tulajdonsága" alkalmazható. Algebrai nyelven ez a + b = b + a {\displaystyle a+b=b+a} 
.
Figyeljük meg, hogy ez nem vonatkozik a kivonásra! (azaz a - b ≠ b - a {\displaystyle a-b\neq b-a} 
)
A szorzás kommutatív tulajdonsága
Ha két tag operátora szorzás, akkor a "szorzás kommutatív tulajdonsága" alkalmazható. Algebrai nyelven ez a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} 
.
Vegye figyelembe, hogy ez nem vonatkozik az osztásra! (azaz a b ≠ b a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}}} 
, amikor a ≠ b {\displaystyle a\neq b} 
)
Az összeadás asszociatív tulajdonsága
Az "asszociatív" a számok csoportosítására utal. Az összeadás asszociatív tulajdonsága azt jelenti, hogy három vagy több tag összeadásakor nem számít, hogy ezek a tagok hogyan vannak csoportosítva. Algebrailag ez a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} 
. Vegyük észre, hogy ez nem érvényes a kivonásra, pl. 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} 
(lásd a disztributív tulajdonságot).
A szorzás asszociatív tulajdonsága
A szorzás asszociatív tulajdonsága azt jelenti, hogy három vagy több tag szorzásakor nem számít, hogy ezek a tagok hogyan vannak csoportosítva. Algebrailag ez a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} 
. Megjegyezzük, hogy ez nem érvényes az osztásra, pl. 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} 
.
Elosztói tulajdonság
A disztributív tulajdonság kimondja, hogy egy számnak egy másik kifejezéssel való szorzása osztható. Például: a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} 
. (Ezt ne keverjük össze az asszociatív tulajdonságokkal! Például a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} 
.).
Additív azonossági tulajdonság
Az "azonosság" egy szám azon tulajdonságára utal, hogy egyenlő önmagával. Más szóval, létezik két számnak olyan művelete, hogy az összeg változójával egyenlő. Az additív azonossági tulajdonság azt mondja ki, hogy bármely szám és 0 összege az a szám: a + 0 = a {\displaystyle a+0=a} 
. Ez a kivonásra is érvényes: a - 0 = a {\displaystyle a-0=a} 
.
Multiplikatív azonossági tulajdonság
A multiplikatív azonossági tulajdonság azt mondja ki, hogy bármely szám és 1 szorzata az a szám: a ⋅ 1 = a {\displaystyle a\cdot 1=a} 
. Ez az osztásra is érvényes: a 1 = a {\displaystyle {\frac {a}{1}}=a} 
.
Additív inverz tulajdonság
Az additív inverz tulajdonság az additív azonossági tulajdonság ellentéte. Ha egy művelet egy szám és az ellentettjének összege, és az egyenlő 0-val, akkor az a művelet érvényes algebrai művelet. Algebrailag ez a következő: a - a = 0 {\displaystyle a-a=0} 
. Az 1 additív inverze a (-1).
Multiplikatív inverz tulajdonság
A multiplikatív inverz tulajdonság azt jelenti, hogy ha egy művelet egy szám és annak reciprokának a szorzata, és az egyenlő 1-gyel, akkor az a művelet érvényes algebrai művelet. Algebrailag ez a következő: a a = 1 {\displaystyle {\frac {a}{a}}=1} 
. A 2 multiplikatív inverze 1/2.
Haladó algebra
Az "elemi algebra", vagyis az alapalgebra mellett léteznek az algebra olyan, főiskolákon és egyetemeken oktatott haladó algebrai formái, mint az absztrakt algebra, a lineáris algebra és az univerzális algebra. Ide tartozik az is, hogyan lehet mátrixot használni egyszerre sok lineáris egyenlet megoldására. Az absztrakt algebra az egyenletekben található dolgok tanulmányozása, a számokon túlmenően a számcsoportokkal való elvontabbá válás.
Sok matematikai feladat a fizikáról és a mérnöki tudományokról szól. Sok ilyen fizikai problémában az idő egy változó. Az idő a t betűt használja. Az algebra alapgondolatainak használata segíthet egy matematikai problémát a legegyszerűbb formájára redukálni, ami megkönnyíti a nehéz problémák megoldását. Az energia az e, az erő az f, a tömeg az m, a gyorsulás az a, a fénysebesség pedig néha a c. Ezt használják néhány híres egyenletben, mint például az f = ma és az e=mc^2 (bár ez utóbbi egyenlet felállításához az algebránál bonyolultabb matematikára volt szükség).
Kapcsolódó oldalak
- A matematikai témák listája
- Műveleti sorrend
- Parabola
- Számítógépes algebrai rendszer
Kérdések és válaszok
K: Mi az algebra?
V: Az algebra a matematika egy olyan része, amely változókat használ egy még nem ismert érték ábrázolására.
K: Mit jelent az egyenlőségjel az algebrában?
V: Az egyenlőségjel (=) egy egyenletet jelöl az algebrában.
K: Mi az a függvény az algebrában?
V: A függvény az algebrában az egyenletek egy speciális típusa, amely mindig egy bemenetet alakít át egy kimenetté.
K: Hogyan használható az algebra valós problémák megoldására?
V: Az algebra azért használható valós problémák megoldására, mert az algebra szabályai a valós életben is működnek, és a számok felhasználhatók valós dolgok értékeinek ábrázolására. A fizika, a mérnöki tudományok és a számítógépes programozás olyan területek, amelyek folyamatosan használják az algebrát. A földmérésben, az építőiparban és az üzleti életben, különösen a könyvelésben is hasznos az algebra ismerete.
K: Milyen matematikai műveleteket használnak az algebrában a számokkal?
V: Az algebrában az emberek a számokra vonatkozó szabályokat és matematikai műveleteket, például az összeadást, kivonást, szorzást és osztást használják a számokon. A fejlettebb műveletek az exponensekkel kapcsolatosak, kezdve a négyzetekkel és a négyzetgyökkel.
K: Milyen példákat használnak az algebrában használt egyenletekre?
V: Az algebrában használt egyenletek példái közé tartoznak a lineáris egyenletek (egy egyenes egyenlete) és a négyzetes egyenletek, amelyekben a változók négyzetre vannak szorozva (önmagukkal szorozva).
