Matematikai egyenlőtlenségek: definíció és jelölések
Ismertető a matematikai egyenlőtlenségek definíciójáról és jelöléseiről: <, >, ≤, ≥ magyarázata példákkal és gyakorlati alkalmazásokkal.
Az egyenlőtlenség általános értelemben azt az állítást jelenti, hogy két mennyiség nem azonos: az egyik lehet kisebb vagy nagyobb a másiknál, illetve ezekhez kapcsolódó, nem szigorú viszonyok is fennállhatnak. Az egyenlőtlenségek jelölése és alapvető tulajdonságai fontosak a matematika sok területén (algebra, analízis, számelmélet, stb.). Az alábbiakban rövid, közérthető magyarázat és gyakorlati szabályok következnek.
Jelölések és alapfogalmak
Az alábbi lista az alapvető jelöléseket és jelentésüket mutatja:
Az egyenlőtlenség az, amikor az egyik tárgy:
- kisebb, mint a másik ( a < b {\displaystyle \ a<b} azt jelenti,
hogy a kisebb, mint b)
- nagyobb, mint a másik ( a > b {\displaystyle \ a>b} azt jelenti
, hogy a nagyobb, mint b)
- nem kisebb a másiknál ( a ≥ b {\displaystyle a\geq b}
azt jelenti, hogy a nem kisebb b-nél, azaz vagy nagyobb, vagy egyenlő b-vel).
- nem nagyobb, mint a másik ( a ≤ b {\displaystyle a\leq b}
azt jelenti, hogy a nem nagyobb, mint b, vagy kisebb vagy egyenlő b-vel).
Az egyenlőtlenséget néha arra az állításra használják, hogy az egyik kifejezés kisebb, nagyobb, nem kisebb vagy nem nagyobb, mint a másik.
Szigorú és nem szigorú egyenlőtlenségek
- Szigorú egyenlőtlenségek: a < b és a > b. Ezek kizárják az egyenlőséget.
- Nem szigorú egyenlőtlenségek: a ≤ b és a ≥ b. Ezek engedik az egyenlőséget is (azaz lehet, hogy a = b).
Alapvető műveleti szabályok egyenlőtlenségekkel
- Összeadás és kivonás: Ha a < b, akkor tetszőleges valós c-vel a + c < b + c. (Az egyenlőtlenség iránya változatlan.)
- Szorzás pozitív számmal: Ha k > 0 és a < b, akkor k·a < k·b. (Irány megmarad.)
- Szorzás negatív számmal: Ha k < 0 és a < b, akkor k·a > k·b. (Irány megfordul — fontos szabály.)
- Reciprálás (pozitív számokra): Ha 0 < a < b, akkor 1/a > 1/b (az irány megfordul).
- Transzitivitás: Ha a < b és b < c, akkor a < c. Ugyanez igaz ≤ esetén is.
- Összevonás: Ha a ≤ b és b ≤ c, akkor a ≤ c.
Intervallumok és egyenlőtlenségek
Egyenlőtlenségeket gyakran írunk intervallumok formájában:
- (a, b): nyílt intervallum — az értékek nagyobbak, mint a és kisebbek, mint b (szigorú egyenlőtlenség: a < x < b).
- [a, b]: zárt intervallum — beleértve a határértékeket is (nem szigorú: a ≤ x ≤ b).
- [a, b): félnyitott intervallum — a ≤ x < b, stb.
Példák és gyakorlati megoldások
- Példa: Oldjuk meg az egyenlőtlenséget 2x - 3 < 5.
- Adjunk hozzá 3-at: 2x < 8.
- Osszunk 2-vel (pozitív): x < 4.
- Példa: Oldjuk meg -3x ≥ 6.
- Osszunk -3-mal: mivel negatív számmal osztunk, az egyenlőtlenség iránya megfordul: x ≤ -2.
Hasznos megjegyzések
- Az egyenlőtlenségek manipulálásakor mindig figyelj a szorzás/osztás előjelére — ha negatív számmal végzel ilyen műveletet, az irány megfordul.
- Szigorú és nem szigorú esetek külön kezelendők: amikor egyenlőséget is megengedünk (≤, ≥), más eredmény lehet határeseteknél.
- A transzitivitás és az intervallumok használata segíti az összetettebb egyenlőtlenségek összevonását és átlátható leírását.
Az egyenlőtlenségek alapjai gyakran előfordulnak a mindennapi problémamegoldásban és a matematikai bizonyításokban. Ha szeretnél, megmutatok több példát vagy gyakorlatot egy adott típusú egyenlőtlenségre (lineáris, racionális, négyzetes stb.).
Munka egyenlőtlenségekkel
Az egyenlőtlenség a matematikában az, amikor két megoldást vagy választ hasonlítunk össze a nagyobb, mint vagy a kisebb, mint. Ez az, amikor a két vagy még sok megoldás összehasonlítása nem egyenlő mennyiségű. Egy egyenlőtlenség megoldása azt jelenti, hogy megtaláljuk a megoldásait. Ha egy változót egy számmal helyettesítesz, és az állítás igaz, akkor ez egy megoldás. Amikor egy számot behelyettesít egy változóba, és az állítás nem igaz, akkor a szám nem megoldása az állításnak.
Az egyenlőtlenség egy adott változóra való megoldás megtalálása. Egy halmaz relatív sorrendjének megtalálása. Az egyenlőtlenségnek sok megoldása van, de meg kell találni a valódi megoldásokat. Az egyenlőtlenség valós számok megoldása. Az egyenlőtlenséget balról jobbra kell helyesen olvasni, ugyanúgy, mint a többi egyenletet, csak az a különbség, hogy minden egyenletre más szabályok vonatkoznak.
Például x+4>12, ahol x egy valós szám. Először meg kell találni az x-et, és tudni kell, hogy ez a megoldás. A válasz x>8 lesz, és ez egy igaz állítás. Ez a kifejezés az x helyéről szól a valós számok halmazán belül. A számegyenes az egyik módja annak, hogy megmutassuk az összes többi valós számhoz viszonyított helyét (lásd az 1. egyenlőtlenség ábrát).
.jpg)
Egyenlőtlenség 1 Ez a megoldás az x+4>12 egyenletre.
Különböző típusú egyenlőtlenségek
Az egyenlőtlenségeknek öt különböző fajtája létezik:
- Az első a lineáris egyenlőtlenségek, amelyek olyan egyenlőtlenségek, amelyek a kifejezéseket kisebb vagy egyenlő, kisebb vagy nagyobb vagy egyenlő, nagyobb, mint. Ez az egyik, hogy ha az egyenlőtlenséget az egyenlőségi relációra cseréljük, akkor az eredmény egy lineáris egyenlet lesz.
- A második az egyenlőtlenségek kombinációi, amelyek az egyenlőtlenségek kielégítéséhez a megoldási halmazokban kell lennie egy számnak, így az egyenlőtlenségeket kielégítő számok a két megoldási halmaz kereszteződésében lévő értékek lesznek.
- A harmadik az abszolút értékeket tartalmazó egyenlőtlenségek, ami azt jelenti, hogy az értékek átfogalmazhatók olyan egyenlőtlenségek kombinációjaként, amelyek abszolút értékeket tartalmaznak.
- A negyedik az úgynevezett polinomiális egyenlőtlenségek azt jelenti, hogy folyamatos, ez azt jelenti, hogy a grafikonjaiknak nincsenek ugrások vagy törések.
- Végül, de nem utolsósorban a racionális egyenlőtlenségek, ami azt jelenti, hogy az egyik polinom osztva egy polinommal. Más szóval, a racionális függvénygrafikonok nem rendelkeznek törésekkel, és nem képviselik a nevező nullpontjainál.
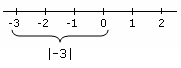
abszolút érték Abszolút értéket mutató példa
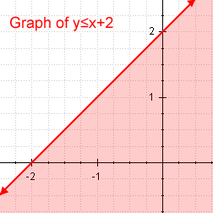
Lineáris egyenlőtlenség Példa a lineáris egyenlőtlenségre
Az egyenlőtlenségek megoldásának négy módja
Négyféleképpen lehet kvadratikus egyenleteket megoldani:
- Az első számú szabály az, hogy mindkét oldalon ugyanazt a számot kell hozzáadni vagy kivonni.
- A második szabály az, hogy az oldalakat el kell tolni, és meg kell változtatni az egyenlőtlenség előjelének helyét.
- A harmadik szabály az, hogy szorozni kell.
- A negyedik szabály az, hogy ugyanazt a pozitív vagy negatív számot kell elosztani mindkét oldalra. Ezeket azonban csak könnyű egyenlőtlenségi problémáknál használhatod.
Továbbá, egy egyenlőtlenség megoldásához két lépés szükséges. Az első az összeadás vagy kivonás reciprokával történő egyszerűsítés. A második lépés a szorzás vagy osztás reciprokával történő további egyszerűsítés. Amikor egy egyenlőtlenséget negatív számmal szorzunk vagy osztunk, ne feledjük, hogy az egyenlőtlenség szimbólumát megfordítjuk.

példa az egyenlőtlenségek szorzatára

Egy példa az egyenlőtlenségek összeadására.
Példák egyenlőtlenségek megoldására
Az egyenlőtlenség olyan matematikai kijelentés, amely megmagyarázza, hogy a két érték nem egyenlő és nem különbözik egymástól. Az ab egyenlet azt jelenti, hogy a nem egyenlő b-vel. Az egyenlőtlenség ugyanaz, mint bármelyik egyenlet, de az egyetlen különbség az, hogy az egyenlőtlenség nem használ egyenlőségjelet, hanem szimbólumokat használ. A b>a egyenlőtlenség azt jelenti, hogy b nagyobb, mint a. A sebességhatárok,a jel és mások kifejezésére egyenlőtlenséget használnak.
Egy egyenlőtlenség megoldása során egy személynek igaz állítással kell rendelkeznie. Ha egy egyenlőtlenséget úgy osztasz vagy szorzol, hogy mindkét oldalán negatív szám van, akkor az állítás hamis.Ahhoz, hogy az állítás negatív számmal helyes legyen, meg kell fordítanod a szimbólumot, hogy az állítás helyes legyen. Ha egy szám pozitív szám, akkor nem kell megfordítani a szimbólumot. Az egyenlőtlenség az igaz állítás igazzá tételéről szól.
Kezdjük például egy igaz állítással -6y<-12. Ha mindkét oldalt elosztjuk -6-tal, akkor az eredmény y<2 lesz. Ebben az állításban a szimbólumot meg kell fordítani ahhoz, hogy igaz állítást kapjunk, y>2 a helyes válasz. A számegyenesen (lásd a 2. egyenlőtlenség ábrát) egy zárt árnyékolt kör jelzi, hogy szerepel a megoldáshalmazban. A nyitott kör arra utal, hogy nem szerepel a megoldáshalmazban.
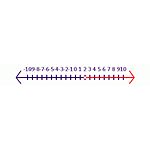
2. egyenlőtlenség A -6y<-12 egyenlet megoldása
Kapcsolódó oldalak
- Egyenlőség (matematika)
- Egyenlet
Kérdések és válaszok
K: Mit jelent az, hogy "a < b"?
V: Azt jelenti, hogy a kisebb, mint b.
K: Mit jelent az, hogy "a > b"?
V: Azt jelenti, hogy a nagyobb, mint b.
K: Mit jelent az "a ≥ b"?
V: Azt jelenti, hogy a nem kisebb, mint b, azaz vagy nagyobb, vagy egyenlő b-vel.
K: Mit jelent az "a ≤ b"?
V: Azt jelenti, hogy a nem nagyobb, mint b, vagy kisebb, vagy egyenlő b-vel.
K: Hogyan használhatjuk az egyenlőtlenséget a matematikában?
V: Az egyenlőtlenséget arra az állításra lehet használni, hogy az egyik kifejezés kisebb, nagyobb, nem kisebb vagy nem nagyobb, mint a másik.
Keres