Szorzás (multiplikáció): definíció és alapvető tulajdonságok

Szorzás (multiplikáció): alapfogalmak, szabályok és példák — commutatívitás, valós/komplex számok, ismételt összeadás és gyakorlati alkalmazások érthetően és példákkal.

A szorzás két szám szorzatának meghatározására szolgáló számtani művelet. A szorzást a tanulási sorrendben általában az összeadás és a kivonás után tárgyalják.

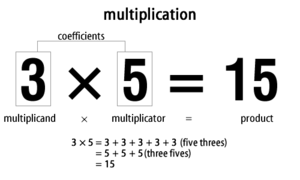
Természetes számokkal végzett szorzás egyszerűen megadja, hogy hány egységnyi lap található egy téglalapban, ha az egyik oldal egységeinek száma megegyezik az egyik tényezővel, a másik oldal egységeinek száma pedig a másik tényezővel. Így például egy 3 egység × 5 egység oldalhosszúságú téglalapban 3 × 5 = 15 egységnyi négyzet található.

Valós számokkal a szorzás azonosítható a téglalap területével: ha az egyik oldal hossza az egyik szám, a másik oldal hossza a másik szám, akkor a téglalap területe a két szám szorzatával adódik.

Például a három szorozva öttel ugyanaz, mint ötször három: 3 × 5 = 15. Ugyanezt mondhatjuk így is: "háromszor öt egyenlő tizenöt". A matematikusok a szorozni kívánt két számot együtt gyakran együtthatóknak nevezik, illetve külön-külön "szorzandó" és "szorzó" a terminológia: szorzandó × szorzó = szorzat..

A szorzás sok számtartományban kommutatív: a tényezők sorrendje nem befolyásolja az eredményt. Ez így van az egész számokra, a racionális számokra, az összes valós számra, valamint a komplex számokra. Nem általánosan igaz azonban minden algebrai struktúrában: a szorzás nem feltétlenül kommutatív például a kvaterniókon (kvaternerionokra — a négydimenziós térben ábrázolható számok), a vektorokra (a vektorszorzatoknál a fajta szorzat dönt: a skaláris (dot) szorzat commutatív, a kereszt (cross) szorzat antikommutatív), és a mátrixokra.

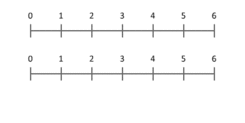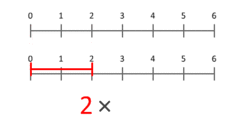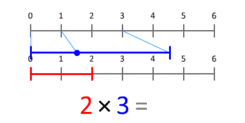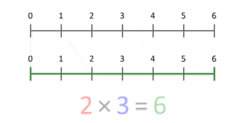
A szorzás egyszerű fogalmilag leírható ismételt összeadásként a nemnegatív egészekre: m × n azt jelenti, hogy m-et n-szer adunk össze. Ez a szemlélet segít a kardinális számok szorzásának halmazelméleti értelmezésében (a Descartes-féle szorzat vagy karteziánus szorzat alapján |A×B| = |A|·|B|). Pontosabb fizikai szemlélet a mennyiségek skálázása: a szorzás egy hosszúság vagy mennyiség felnagyítását/kicsinyítését jelenti. Az egyszerű animációk gyakran azt mutatják be, hogy pl. a 3-at megszorozva 2-vel a skálázás eredménye 6: a 3 hosszúságú szakasz egy pontja a skálázás után a 2 hosszúságú szakasz végére kerül. Ez a szemlélet kiterjeszthető frakciókra és negatív értékekre is (irányokkal együtt).

A szorzás ellentéte az osztás, amely a szorzás inverzművelete (ha lehetséges, azaz nem nullával osztunk).

Alapvető tulajdonságok és szabályok

• Kommutativitás: a × b = b × a (különösen igaz számoknál: egész, racionális, valós, komplex).
• Associativitás: (a × b) × c = a × (b × c). Ez lehetővé teszi, hogy több tényező szorzatát tetszőleges csoportosítással számítsuk ki.
• Disztributivitás az összeadás fölött: a × (b + c) = a × b + a × c, illetve (a + b) × c = a × c + b × c.
• Neutrális elem (egységeleme): 1 a multiplikatív egység: 1 × a = a × 1 = a.
• Nulla tulajdonsága: 0 × a = a × 0 = 0 (a nulla "kioltja" a szorzást).
• Multiplikatív inverz: ha a ≠ 0 (a adott tartományban van inverze), létezik a^{-1} úgy, hogy a × a^{-1} = 1. A testekben (field) minden nemnulla elemnek van inverze.
• Elvonási szabályok és előjelszabályok: (+a)(+b)=+ab, (+a)(-b)=-ab, (-a)(-b)=+ab. Tehát két negatív szorzata pozitív.
• Szorzás és hatványozás: a^n jelöli az a szám n-szeres önszorzatát (n pozitív egész esetén). A hatványozásra vonatkozó szabályok a szorzás szabályaiból következnek: a^m × a^n = a^{m+n} stb.
• Cancelláció: ha a × b = a × c és a ≠ 0, akkor b = c (ez azonban nem áll fenn gyűrűkben, ahol lehetnek nullosztók).

Gyakorlati példák

• Disztributivitás: 3 × (4 + 5) = 3 × 9 = 27, és 3 × 4 + 3 × 5 = 12 + 15 = 27.
• Előjelszabály: (-2) × 3 = -6, (-2) × (-3) = 6.
• Nulla: 0 × 7 = 0.
• Inverz: 5 × (1/5) = 1 (a racionális számok között).

Jelölések és kiterjesztések

• Jelölések: a szorzatot jelölhetjük ×, · vagy egyszerűen szóközzel (ab), illetve számítástechnikában gyakran *-tal.
• Általános algebrai rendszerek: a szorzás definíciója és tulajdonságai eltérhetnek gyűrűkben, testekben (field), komponensenkénti műveleteknél, mátrixoknál stb. Például egy mátrixszorzás általában nem kommutatív, és létezhetnek nullosztók gyűrűkben.
• Vektorok: a skalárszorzás (skalár × vektor) lineáris skálázás; a vektorok közötti szorzat többféle lehet (dot, cross), és ezeknek különböző algebrai tulajdonságaik vannak.
• Kardinális számok: halmazelméletben |A×B| = |A|·|B| adja meg a Descartes-féle szorzat kárdinalitását.

Megjegyzések

• A szorzás megértése több szemlélettel (ismételt összeadás, geometriai terület, skálázás, halmazelméleti kartéziánus szorzat) segíti a különböző alkalmazások közötti átmenetet.
• Halmaz- és algebraelméleti kontextusban mindig érdemes megadni, hogy mely strukturális tulajdonságok (kommutativitás, egységelem, inverzok, nullosztók) érvényesek az adott környezetben.

Kérdések és válaszok

Q: Mi az a szorzás?

K: Hogyan hívják a két szorzandó számot?

K: A szorzás kommutatív?

K: Hogyan értelmezhetjük a kardinális számok szorzatát?

K: Hogyan ábrázoljuk a három és öt szorzatát?

K: Mi a szorzás ellentéte?

Keresés betűvel