Függvény (matematika)
A matematikában a függvény egy olyan matematikai objektum, amely egy bemenetre adott kimenetet állít elő - ez lehet egy szám, egy vektor vagy bármi, ami egy halmazon belül létezhet.
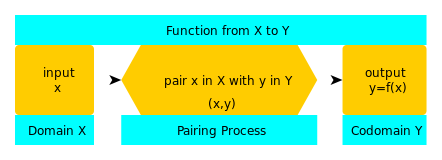
Tehát egy függvény olyan, mint egy gép, amely x értékeket vesz fel, és y kimenetet ad vissza. x összes lehetséges értékének halmazát nevezzük tartománynak. Azt a halmazt, amely minden olyan értéket tartalmaz, amelyet y felvehet, kodomainnek nevezzük.
Ha ez megtörténik, akkor azt mondjuk, hogy y az x függvénye, és azt írjuk, hogy y =f(x). f a függvény neve, és azt írjuk, hogy f : X → Y {\displaystyle f:X\to Y} 
(függvény X-ből Y-ba), hogy a függvény három részét ábrázoljuk: a tartományt (x), a társtartományt (y) és a párosítási folyamatot (a nyilat).
Egy példa egy függvényre: f(x)=x+1 Adunk egy természetes x {\displaystyle x}
(0,1,2,3...) számot, és kapunk egy természetes y {\displaystyle y} számot. 
, amely x {\displaystyle x} +1 (1,2,3,4...) A függvény gondolatát úgy állítottuk fel, hogy mindenféle lehetőséget lefedjen. A függvénynek nem kell egyenletnek lennie. A fő gondolat az, hogy a bemenetek és a kimenetek valahogy párosítva legyenek, még akkor is, ha a folyamat nagyon bonyolult.
Metaforák
Táblák
A bemeneteket és kimeneteket a képhez hasonló táblázatba lehet tenni; ez egyszerű, ha nincs túl sok adat.
Grafikonok
A képen látható, hogy a 2 és a 3 is párosítva van a c-vel; ez a másik irányban nem megengedett, a 2 nem adhatná ki a c-t és a d-t,minden bemenetnek csak egy kimenete lehet. Az összes f ( x ) {\displaystyle f(x)} 
(a képen c és d) általában az f {\displaystyle f}
képhalmazának nevezzük, és a képhalmaz lehet az egész kodomain vagy nem. Mondhatjuk, hogy a kodomain A részhalmaza a képhalmazzal f(A). Ha a bemeneteknek és a kimeneteknek van egy sorrendje, akkor könnyen ábrázolhatjuk őket egy gráfban:
Így a kép jön a képen a képet a halmaz A. Ez teszi a mind a 2 és 3 van párosítva nem megengedett a másik irányba,még lehet, hogy a kodomain között vagy sem. Megállapítható, hogy a kodomain A részhalmaza a képhalmaz F(A).
Történelem
Az 1690-es években Gottfried Leibniz és Johann Bernoulli használták a függvény szót betűkkel egymás között, így a modern fogalom a számítással egy időben kezdődött.
1748-ban Leonhard Euler adta: "Egy változó mennyiség függvénye olyan analitikus kifejezés, amely a változó mennyiségből és számokból vagy állandó mennyiségekből bármilyen módon összeáll." majd 1755-ben: "Ha egyes mennyiségek úgy függenek más mennyiségektől, hogy ha az utóbbiakat megváltoztatjuk, akkor az előbbi mennyiségeket az utóbbiak függvényeinek nevezzük. Ez a meghatározás meglehetősen széles körben alkalmazható, és minden olyan módot magában foglal, ahogyan az egyik mennyiséget a másik meghatározhatja. Ha tehát x egy változó mennyiséget jelöl, akkor minden olyan mennyiséget, amely x-től bármilyen módon függ, vagy általa meghatározott, x függvényeinek nevezünk." ami nagyon modern.
Általában Dirichletnek tulajdonítják azt a változatot, amelyet a 20. század második feléig az iskolákban használtak: "y egy x változónak az a < x < b intervallumon definiált függvénye, ha az x változó minden értékének ezen az intervallumon belül megfelel az y változó egy meghatározott értéke." Az sem lényeges, hogy milyen módon jön létre ez a megfeleltetés."
1939-ben Bourbaki általánosította a Dirichlet-féle definíciót, és a definíció halmazelméleti változatát a bemenetek és kimenetek közötti megfeleltetésként adta meg; ezt körülbelül 1960-tól használták az iskolákban.
Végül 1970-ben Bourbaki megadta a modern definíciót, mint f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} hármasát. 
, ahol F ⊂ X × Y , ( x , f ( x ) ) ∈ F {\displaystyle F\subset X\times Y,(x,f(x))\ in F}
(azaz f : X → Y {\displaystyle f:X\to Y} és F = { ( x , f ( x ) ) ) | x ∈ X , f ( x ) ∈ Y } {\displaystyle F=\{(x,f(x))|x\in X,f(x)\in Y\}} 
).
Funkciótípusok
- Elemi függvények - Az iskolában általában tanult függvények: törtek, négyzetgyök, szinusz, koszinusz és érintő függvények és néhány más függvény.
- Nem elemi függvények - A legtöbbjük nem használ olyan műveleteket, amelyeket nem tanulunk az iskolában (mint például + vagy -, vagy hatványok). Sok integrál nem elemi függvény.
- Inverz függvények - Olyan függvények, amelyek egy másik függvényt visszavonnak. Például: ha F(x) az f(x)=y inverze, akkor F(y)=x. Nem minden függvénynek van inverze.
- Különleges funkciók: Névvel rendelkező függvények. Például: szinusz, koszinusz és érintő. Az olyan függvényeket, mint f(x)=3x (háromszor x) nem nevezzük speciális függvényeknek. Ezek lehetnek elemi, nem elemi vagy inverz függvények.
Kérdések és válaszok
K: Mi a függvény a matematikában?
V: A függvény a matematikában egy olyan objektum, amely egy bemenetre adott kimenetet állít elő, ami lehet szám, vektor vagy bármi, ami egy halmazon belül létezhet.
K: Mi az a két halmaz, amely a függvényekhez kapcsolódik?
V: Az összes olyan érték halmazát, amelyet x felvehet, tartománynak nevezzük, az összes olyan értéket tartalmazó halmazt pedig, amelyet y felvehet, kodomainnek.
K: Hogyan jelölik gyakran a függvényeket?
V: A függvényeket gyakran dőlt betűkkel jelölik, például f, g, h.
K: Hogyan ábrázolunk egy függvényt?
V: Egy függvényt úgy ábrázolunk, hogy y = f(x), ahol f a függvény neve, és azt írjuk, hogy f : X → Y (függvény X-ből Y-ba), hogy a függvény három részét - tartomány (X), kodomain (Y) és párosítási folyamat (a nyíl) - ábrázoljuk.
K: Tudna példát mondani egy függvényre?
V: Egy függvényre példa az f(x) = x + 1. Az ember bemenetként megad egy x természetes számot, és megkapja az y természetes számot, amely x + 1. Ha például 3-at adunk az f függvénynek bemenetként, akkor a kimenet 4 lesz.
K: Minden függvénynek egyenletnek kell lennie?
V: Nem, nem minden függvénynek kell egyenletnek lennie. A függvények lényege, hogy a bemenetek és a kimenetek valahogyan párosítva vannak - még ha ez nagyon bonyolult is lehet.
