Algoritmus

Algoritmusok összehasonlítása

Egy probléma megoldására általában többféle megoldás létezik. Sokféle recept létezhet egy bizonyos étel elkészítésére, amely másképp néz ki, de végül ugyanolyan ízű lesz. Ugyanez igaz az algoritmusokra is. Azonban ezek közül néhány módszer jobb lesz, mint mások. Ha egy recepthez sok bonyolult hozzávalóra van szükség, amelyekkel nem rendelkezel, akkor nem olyan jó, mint egy egyszerű recept. Amikor az algoritmusokat mint a problémák megoldásának módját vizsgáljuk, gyakran azt szeretnénk tudni, hogy mennyi idő alatt oldaná meg a számítógép a problémát egy adott algoritmus segítségével. Amikor algoritmusokat írunk, azt szeretnénk, ha az algoritmusunk a lehető legkevesebb időt venné igénybe, hogy a lehető leggyorsabban megoldhassuk a problémánkat.

A főzésben egyes recepteket nehezebb elkészíteni, mint másokat, mert több időt vesz igénybe a befejezésük, vagy mert több dolgot kell szem előtt tartani. Ugyanez a helyzet az algoritmusok esetében is, és az algoritmusok akkor jobbak, ha a számítógép számára könnyebben kivitelezhetőek. Azt, ami egy algoritmus nehézségét méri, komplexitásnak nevezzük. Amikor azt kérdezzük, hogy mennyire bonyolult egy algoritmus, gyakran azt szeretnénk tudni, hogy mennyi időbe telik egy számítógépnek megoldani azt a problémát, amit meg akarunk oldani vele.

Rendezés

Ez egy példa egy algoritmusra, amely a színekkel ellátott kártyákat azonos színű kupacokba rendezi:

1. Vegye fel az összes kártyát.
2. Válasszon ki egy kártyát a kezéből, és nézze meg a kártya színét.
3. Ha már van egy halom ilyen színű kártya, akkor ezt a kártyát tegye arra a halomra.
4. Ha nincs ilyen színű kártyakupac, készítsen egy új kupacot csak ebből a színből.
5. Ha még mindig van kártya a kezedben, térj vissza a második lépésre.
6. Ha nincs még kártya a kezedben, akkor a kártyákat kiválogatod. Végeztél.

Rendezés számok szerint

Ezek példák olyan algoritmusokra, amelyek egy sok különböző számot tartalmazó kártyakupac rendezésére szolgálnak úgy, hogy a számok sorrendben legyenek.

A játékosok egy halom kártyával kezdenek, amelyeket még nem válogattak szét.

Első algoritmus

Ez az algoritmus egyszerre egy-egy kártyalapon megy végig. Ezt a kártyát összehasonlítja a következő kártyával a veremben. Vegye figyelembe, hogy ez a pozíció csak a 6. lépésben változik. Ezt az algoritmust buborékrendezésnek nevezzük. Lassú.

1. Ha a kártyakupac üres, vagy csak egy kártyát tartalmaz, akkor a kártyák rendezettek; végeztél.
2. Fogd a kártyakupacot. Nézd meg a pakli első (legfelső) lapját.
3. A kártya, amelyet nézel, az A kártya. Az A kártya jelenlegi helye a P halomban van.
4. Ha az A kártya után nincs több kártya a pakliban, lépjen a 8. lépésre.
5. A következő kártya a pakliban a B kártya.
6. Ha a B kártya száma alacsonyabb, mint az A kártyaé, cserélje fel az A és a B kártya helyét. Amikor kártyákat cserélsz, ne változtasd meg a P pozíciót.
7. Ha a P pozíció után van még egy kártya a pakliban, nézze meg; térjen vissza a 3. lépéshez.
8. Ha az utolsó körben nem cserélte fel egyetlen kártya pozícióját sem, akkor végeztünk; a kártyapakli rendezett.
9. Ellenkező esetben térjen vissza a 2. lépéshez.

Lépésről-lépésre példa

Vegyük az "5 1 4 2 8" számokat tartalmazó kártyalapokat, és a legkisebb számtól a legnagyobbig rendezzük őket ezzel az algoritmussal. Az algoritmus minden lépésnél összehasonlítja a félkövérrel írt elemeket. A kártyakupac teteje a bal oldalon van.

Első lépés:
( 5 1 4 2 8 ) → {\displaystyle \to } ( 1 5 4 2 8 ) Itt az algoritmus összehasonlítja az első két elemet, és felcseréli őket.
( 1 5 4 2 8 ) → {\displaystyle \to } ( 1 4 5 2 8 )
( 1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 ) Ezek az elemek már sorrendben vannak, ezért az algoritmus nem cseréli ki őket.
Második lépés:
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Most a kártyapakli már rendezett, de az algoritmusunk ezt nem tudja. Az algoritmusnak egy teljes menetre van szüksége csere nélkül ahhoz, hogy tudja, hogy rendezett.
Harmadik lépés:
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Végül a tömb rendezve van, és az algoritmus megállhat.

Történelem

Ez egy könnyen érthető algoritmus a rendezéshez. Az informatikusok Bubble sortnak nevezték el, mert a kisebb elemek feljebb kerülnek, és minden egyes futtatás során változik a pozíciójuk. Sajnos az algoritmus nem túl jó, mert a rendezéshez hosszú időre van szükség (sok átfutás a kártyakupacon).

Második algoritmus

Ez az algoritmus egy másik ötletet használ. Néha egy probléma megoldása nehéz, de a probléma megváltoztatható, így egyszerűbb, könnyebben megoldható problémákból áll. Ezt nevezzük rekurziónak. Nehezebb megérteni, mint az első példát, de jobb algoritmust ad.

Alapvető elképzelés

1. Ha a kupacban nincs kártya, vagy csak egy kártya van benne, akkor a kupacot kiválogattuk, és kész.
2. Ossza a kártyakupacot két, nagyjából azonos méretű félre. Ha a kártyák száma páratlan, akkor a két halom közül az egyikben egy kártyával több lesz, mint a másikban.
3. Rendezze a két halmot az alábbi algoritmus szerint (Mindkét halom esetében kezdje a lista 1. elemével).
4. Egyesítse a két rendezett halmot az alábbiakban leírtak szerint.
5. Az eredmény egy rendezett kártyakupac. Kész is van.

Két halom összevonása

Ez két kártyapaklival működik. Az egyiket A-nak, a másikat B-nek hívják. Van egy harmadik pakli, amely az elején üres, C. A végén ez tartalmazza az eredményt.

1. Ha az A vagy a B halom üres, akkor a nem üres halom összes kártyáját tegye a C halom tetejére; ezzel kész, a C halom az egyesítés eredménye. (Megjegyzés: fogd az egész paklit, és tedd a C paklira; ha kártyánként csinálod, akkor megváltozik a sorrend, és nem úgy működik, ahogyan kellene).
2. Nézd meg az A és a B halom legfelső lapjait. Tedd a C halom tetejére azt, amelyiknek a száma alacsonyabb. Ha a C halomban nem volt kártya, akkor most egy kártya lesz benne.
3. Ha az A vagy a B halomban maradtak kártyák, térjünk vissza az 1. lépéshez a rendezéshez.

Történelem

John von Neumann 1945-ben fejlesztette ki ezt az algoritmust. Ő nem számok szerinti rendezésnek, hanem Mergesortnak nevezte el. Ez egy nagyon jó algoritmus a rendezéshez, a többihez képest.

Harmadik algoritmus

Az első algoritmusnak sokkal hosszabb ideig tart a kártyák rendezése, mint a másodiknak, de javítható (jobbá tehető). A buborékválogatást vizsgálva észrevehető, hogy a magas számmal rendelkező kártyák elég gyorsan mozognak a verem tetejéről, de a verem alján lévő alacsony számmal rendelkező kártyáknak hosszú időbe telik, amíg felemelkednek (feljebb kerülnek). Az első algoritmus javítására itt az ötlet:

Ahelyett, hogy két egymás mellett lévő kártyát hasonlítanánk össze, a játék elején egy "különleges" kártyát választunk. Ezután az összes többi kártyát ehhez a kártyához hasonlítják.

1. Kezdjük egy A veremmel. Lesz még két másik verem, B és C, amelyeket később hozunk létre.
2. Ha az A halomban nincs kártya, vagy csak egy kártya van benne, akkor befejeztük a rendezést.
3. Egy kártyát választunk az A halomból, lehetőleg véletlenszerűen. Ezt nevezzük pivotnak.
4. Az "A" pakli összes többi lapját ehhez a pivothoz hasonlítjuk. A kisebb számmal rendelkező kártyák a B halomba kerülnek, az azonos vagy nagyobb számmal rendelkező kártyák pedig a C halomba.
5. Ha a B vagy C halomban vannak kártyák, akkor ezeket a halmokat ugyanezzel az algoritmussal kell rendezni (a lista 1. helyén kezdjük a B és a C halom esetében is).
6. Kész. A rendezett kártyakupacban először a B rendezett kupac, majd a pivot, és végül a C rendezett kupac van.

Történelem

Ezt az algoritmust C. A. R. Hoare fejlesztette ki 1960-ban. Ma az egyik legszélesebb körben használt algoritmus a rendezéshez. A neve Quicksort.

Animáció, amely bemutatja, hogyan működik a buborékválogatás


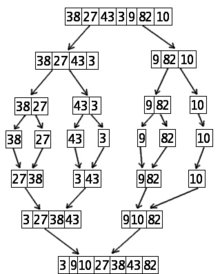
7 számok rendezése a második számok szerinti rendezési algoritmus (Mergesort) segítségével


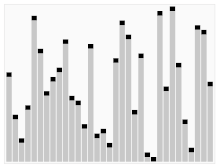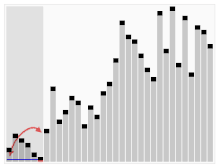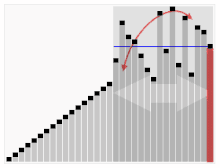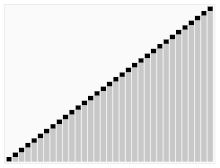
A harmadik algoritmus a kártyák rendezéséhez. A piros sávval jelzett elemet választjuk ki sarkpontnak. Kezdetben ez a jobbra lévő elem. Ezt az algoritmust Quicksortnak nevezik.

Algoritmusok összerakása

Ha a játékosoknak szín- és számkártyáik vannak, akkor szín és szám szerint rendezhetik őket, ha elvégzik a "színek szerinti rendezés" algoritmust, majd elvégzik a "számok szerinti rendezés" algoritmust minden egyes színes halomra, majd összerakják a halmokat.

A számok szerinti rendezési algoritmusok nehezebbek, mint a színek szerinti rendezési algoritmusok, mert előfordulhat, hogy többször is meg kell ismételni a lépéseket. Úgy is mondhatnánk, hogy a számok szerinti rendezés bonyolultabb.

Kapcsolódó oldalak

• Az euklideszi algoritmust több mint 2000 évvel ezelőtt találták meg. Képes két szám legnagyobb közös osztóját megtalálni.