Planck-állandó

Háttér:

A cikkben használt szimbólumok.
Szimbólum Jelentése E Energia h Planck-állandó k Boltzmann-állandó c fénysebesség λ sugárzás hullámhossza ν sugárzási frekvencia T abszolút hőmérséklet

1670 és 1900 között a tudósok a fény természetéről vitatkoztak. Egyes tudósok úgy vélték, hogy a fény sok millió apró részecskéből áll. Más tudósok úgy vélték, hogy a fény hullám.

Fény: hullámok vagy részecskék?

1678-ban Christiaan Huygens megírta a Traité de la lumiere ("Értekezés a fényről") című könyvet. Úgy vélte, hogy a fény hullámokból áll. Azt mondta, hogy a fény nem állhat részecskékből, mert két sugárnyaláb fénye nem verődik vissza egymásról. 1672-ben Isaac Newton megírta az Opticks című könyvet. Úgy vélte, hogy a fény vörös, sárga és kék részecskékből áll, amelyeket ő korpuszoknak nevezett. Newton ezt a "két prizma kísérletével" magyarázta. Az első prizma a fényt különböző színekre bontotta. A második prizma ezeket a színeket fehér fénnyé egyesítette.

A 18. században Newton elmélete kapta a legnagyobb figyelmet. Thomas Young 1803-ban leírta a "kettős rés kísérletet". Ebben a kísérletben a két keskeny résen áthaladó fény interferál önmagával. Ez olyan mintázatot eredményez, amely megmutatja, hogy a fény hullámokból áll. A XIX. század hátralévő részében a fény hullámelméletének szentelték a legnagyobb figyelmet. Az 1860-as években James Clerk Maxwell olyan egyenleteket dolgozott ki, amelyek az elektromágneses sugárzást hullámokként írták le.

Az elektromágneses sugárzás elmélete a fényt, a rádióhullámokat, a mikrohullámokat és sok más hullámtípust ugyanolyan dolognak tekinti, kivéve, hogy különböző hullámhosszúak. A szemünkkel látható fény hullámhossza nagyjából 400 és 600 nm között van. A rádióhullámok hullámhossza 10 m és 1500 m között változik, a mikrohullámok hullámhossza pedig körülbelül 2 cm. Vákuumban minden elektromágneses hullám fénysebességgel terjed. Az elektromágneses hullám frekvenciája a következő:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}}.

A szimbólumok meghatározása itt található.

Fekete testradiátorok

Minden meleg dolog hősugárzást bocsát ki, ami elektromágneses sugárzás. A legtöbb földi dolog esetében ez a sugárzás az infravörös tartományba esik, de ami nagyon forró (1000 °C vagy annál magasabb), az látható sugárzást, azaz fényt bocsát ki. Az 1800-as évek végén számos tudós tanulmányozta a különböző hőmérsékletű fekete testekből származó elektromágneses sugárzás hullámhosszát.

Rayleigh-Jeans törvény

Lord Rayleigh 1900-ban publikálta először a Rayleigh-Jeans-törvény alapjait. Az elmélet a gázok kinetikus elméletén alapult. Sir James Jeans 1905-ben publikálta a teljesebb elméletet. A törvény összefüggésbe hozza a különböző hőmérsékletű fekete testek sugárzói által kibocsátott elektromágneses energia mennyiségét és hullámhosszát. Az ezt leíró egyenlet a következő:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}}.

Hosszú hullámhosszú sugárzás esetén az egyenlet által megjósolt eredmények jól megfeleltek a laboratóriumban kapott gyakorlati eredményeknek. Rövid hullámhosszú sugárzások (ultraibolya fény) esetében azonban az elmélet és a gyakorlat közötti különbség olyan nagy volt, hogy az "ultraibolya katasztrófa" becenevet érdemelte ki.

Planck-törvény

1895-ben Wien közzétette a fekete testek sugárzásával kapcsolatos tanulmányainak eredményeit. Az ő képlete a következő volt:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

Ez a képlet jól működött a rövid hullámhosszú elektromágneses sugárzások esetében, de nem működött jól a hosszú hullámhosszúaknál.

Max Planck 1900-ban publikálta tanulmányainak eredményeit. Megpróbált kifejezést kidolgozni a fekete test sugárzására a hullámhosszban kifejezve, feltételezve, hogy a sugárzás kis kvantumokból áll, majd megvizsgálta, mi történik, ha a kvantumokat végtelenül kicsivé tesszük. (Ez egy szokásos matematikai megközelítés). A kifejezés a következő volt:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}}}.

Ha a fény hullámhosszát nagyon nagyra engedjük, akkor kimutatható, hogy a Raleigh-Jeans- és a Planck-összefüggés majdnem azonos.

Kiszámította h-t és k-t, és megállapította, hogy

h = 6,55×10⁻²⁷ erg-szek.

k = 1,34×10⁻¹⁶erg-deg ^-1.

Az értékek közel állnak a ma elfogadott 6,62606×10⁻³⁴ és 1,38065×10⁻¹⁶ értékekhez. A Planck-törvény jól egyezik a kísérleti adatokkal, de teljes jelentőségét csak évekkel később ismerték fel.

A fény kvantumelmélete

Kiderült, hogy az elektronok a fotoelektromos hatás hatására elmozdulnak, ha a fény elér egy küszöbfrekvenciát. Ez alatt már nem tudnak elektronokat kibocsátani a fémből. Albert Einstein 1905-ben publikálta a hatást magyarázó tanulmányát. Einstein azt javasolta, hogy a fénysugár nem a térben terjedő hullám, hanem különálló hullámcsomagok (fotonok) gyűjteménye, amelyek mindegyike energiával rendelkezik. Einstein szerint a hatás annak köszönhető, hogy egy foton egy elektronba ütközik. Ez a fény részecskejellegét bizonyította.

Einstein azt is megállapította, hogy a nagy hullámhosszú elektromágneses sugárzásnak nincs hatása. Einstein szerint ez azért volt így, mert a "részecskéknek" nem volt elég energiájuk ahhoz, hogy megzavarják az elektronokat.

Plank felvetette, hogy az egyes fotonok energiája a Planck-állandóval függ össze a foton frekvenciájával. Ez matematikailag a következőképpen írható fel:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}}.

Plank 1918-ban kapta meg a Nobel-díjat a fizika fejlődéséhez nyújtott szolgálatai elismeréseként az energiakvantumok felfedezésével. 1921-ben Einstein Nobel-díjat kapott a Planck-állandó és a fotoelektromos hatás összekapcsolásáért.

Az illusztráció Newton eredeti, a Royal Society-nek írt leveléből származik (1671. január 1. [Julián-naptár]). Az S a napfényt jelképezi. A fény a BC és DE síkok között színes. Ezek a színek újra egyesülnek, és a GH síkon a napfényt alkotják.


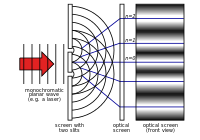
Young kettős réskísérlete


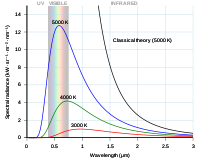
Rayleigh-Jeans-görbe és Planck-görbe a foton hullámhosszának függvényében ábrázolva.


Solway Konferencia 1911. Planck, Einstein és Jeans állnak. Planck balról a második. Einstein a második jobbról. Jeans jobbról az ötödik. Wien ül, jobbról a harmadik.

Alkalmazás

A Planck-állandó számos alkalmazásban fontos. Az alábbiakban néhányat felsorolunk.

Az atom Bohr-féle modell

1913-ban Niels Bohr közzétette az atom szerkezetének Bohr-modelljét. Bohr szerint az atommag körül keringő elektronok szögnyomatéka csak bizonyos értékeket vehet fel. Ezeket az értékeket a következő egyenlet adja meg

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

ahol

L = egy szinthez tartozó forgatónyomaték.

n = pozitív egész szám.

h = Planck-állandó.

Az atom Bohr-modellje segítségével kiszámítható az elektronok energiája az egyes szinteken. Az elektronok általában az atom legalacsonyabb számozású állapotait töltik ki. Ha az atom energiát kap, például elektromos áramtól, az elektronok magasabb állapotba gerjesztődnek. Az elektronok ezután visszahullnak egy alacsonyabb állapotba, és egy foton kibocsátásával elveszítik a felesleges energiájukat. Mivel az energiaszinteknek meghatározott értékei vannak, a fotonok is meghatározott energiaszintekkel rendelkeznek. Az így kibocsátott fényt prizma segítségével különböző színekre lehet osztani. Minden elemnek saját mintázata van. A neon mintázata az alábbiakban látható.

Heisenberg bizonytalansági elve

1927-ben Werner Heisenberg közzétette a bizonytalansági elvet. Az elv kimondja, hogy nem lehet úgy mérést végezni, hogy a mérendő dolgot ne zavarja meg. Egyúttal határt szab a mérés által okozott minimális zavarásnak is.

A makroszkopikus világban ezek a zavarok nagyon kevés különbséget tesznek. Ha például egy folyadékkal teli lombik hőmérsékletét mérjük, a hőmérő a felmelegedés során kis mennyiségű energiát vesz fel. Ez egy kis hibát okoz a végső leolvasásban, de ez a hiba kicsi és nem fontos.

A kvantummechanikában a dolgok másképp állnak. Egyes méréseket a szórt fotonok mintázatának megnézésével végzik. Ilyen például a Compton-szórás. Ha egy részecske helyzetét és impulzusát is mérjük, a bizonytalansági elv szerint kompromisszumot kell kötni az impulzus mérési pontossága és a helyzet mérési pontossága között. Az egyenlet, amely ezt a kompromisszumot leírja, a következő:

Δ x Δ p ≳ h {\displaystyle \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad \qquad }

ahol

Δp = az impulzus bizonytalansága.

Δx = a helyzet bizonytalansága.

h = Planck-állandó.

Fénykibocsátó diódák színe

A jobb oldalon látható elektromos áramkörben a fénykibocsátó diódán (LED) mért feszültségesés a LED anyagától függ. Szilíciumdiódák esetében a feszültségesés 0,6 V. A LED-ek esetében azonban 1,8 V és 2,7 V között van. Ez az információ lehetővé teszi a felhasználó számára a Planck-állandó kiszámítását.

Az egy elektron számára a LED anyagában a potenciális gát átugrásához szükséges energia a következővel adódik

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

ahol

Q_e egy elektron töltése.

V_L a LED-en mért feszültségesés.

Amikor az elektron ismét visszabomlik, egy fényfoton sugárzását váltja ki. A foton energiáját ugyanaz az egyenlet adja meg, mint amit a fotoelektromos hatásnál használunk. Ha ezeket az egyenleteket kombináljuk, akkor a fény hullámhossza és a feszültség a következő módon függ össze

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}}\,}

Ebből az összefüggésből kiszámítható az alábbi táblázat.

Színes	Hullámhossz (nm)	Feszültség
piros fény	650	1.89
zöld fény	550	2.25
kék fény	470	2.62

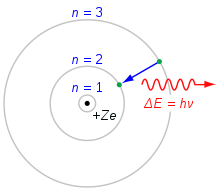
Bohr atommodellje. Az n=3 héjból az n=2 héjba eső elektron energiát veszít. Ez az energia egyetlen foton formájában távozik.


A neon látható spektruma. Minden vonal egy-egy energiaszint-párt jelöl.


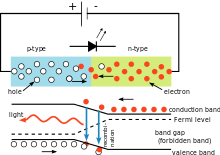
Egyszerű LED áramkör, amely a Planck-állandó használatát szemlélteti. A kibocsátott fény színe a diódán mért feszültségeséstől függ. A fény hullámhossza a Planck-állandó segítségével kiszámítható.

A Planck-állandó értéke és a kilogramm újradefiniálása

Felfedezése óta a h mérése sokkal jobb lett. Planck először 6,55×10 ⁻²⁷erg-szekundumban határozta meg a h értékét. Ez az érték 5%-on belül van a jelenlegi értékhez képest.

2014. március 3-án a h legjobb mérési értéke SI-egységben 6,62606957×10 ⁻³⁴J-s. Az ennek megfelelő érték cgs-egységben 6,6260696957×10 ⁻²⁷erg-szek. A h relatív bizonytalansága 4,4×10 . ⁻⁸

A csökkentett Planck-állandó (ħ) a kvantummechanikában néha használt érték. Meghatározása a következő

ℏ = h 2 π {\displaystyle \hbar ={\frac {h}{2\pi }}}.

A kvantummechanikában az SI helyett néha Planck-egységeket használnak. Ebben a rendszerben a redukált Planck-állandó értéke 1, így a Planck-állandó értéke 2π.

A Plancks-állandó most már nagyon nagy pontossággal mérhető. Ez arra késztette a BIPM-et, hogy fontolóra vegye a kilogramm új meghatározását. A kilogramm meghatározásához többé nem használják a kilogramm nemzetközi prototípusát. Ehelyett a BIPM a Planck-állandó pontos értékét határozza meg. A tudósok ezt az értéket, valamint a méter és a másodperc meghatározását használják a kilogramm meghatározásához.

 

Az elméleti Planck-állandó értéke

A Planck-állandó matematikailag is levezethető:

 

h = μ 0 π 12 c 3 [ q 0 [ 0,9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6,63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{[{q_{0}}}{[0,9163a_{0}]}^{2}]^{2}}}{f_{1r}}}^{5}\cdot {s}=6,63\szor 10^{-34}J\cdot s}

Itt μ 0 {\displaystyle \mu _{0}} a szabad tér permeabilitása, c {\displaystyle c} a fénysebesség, q 0 {\displaystyle q_{0}} az elektron elektromos töltése, a 0 {\displaystyle a_{0}} a Bohr-sugár, és f 1 r {\displaystyle f_{1r}}} az elektron forgási frekvenciája a hidrogénatomban ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3.29\times 10^{15}rev/s)} . Ha ezeket a konstansértékeket behelyettesítjük az elméleti Planck-állandóhoz, akkor az elméleti Planck-állandó értéke pontosan megegyezik a kísérleti értékkel.

Kapcsolódó oldalak

• Hullám-részecske kettősség