Határozatlansági reláció

Diagramok

6. Ez az animáció a világegyetem bizonytalansági természetének egyik fontos következményét mutatja be: az elektronok kvantumalagútját. Nézd meg figyelmesen. Minden alkalommal egy kis darab átjut a gáton.


5. A középső rés rugós mérlegekkel való felfüggesztése lehetővé teszi az impulzus mérését, de ez kiszámíthatatlanul elmozdítja a rést, így az egyes fotonok középen elfoglalt helyére vonatkozó információ elvész.


4. Egy kis lyukkal ellátott akadályra szerelt rugó a részecskét a lyukon keresztülpréseli, ami nyomja az akadályt, megnyújtja a rugót, és így mérhető a lendület. Mivel azonban a rugóra szerelt akadály mozog, kevésbé vagyunk biztosak abban, hogy hol volt a részecske, amikor áthaladt a lyukon, és a diffrakció is befolyásolja a helyzetét az érzékelő képernyőn.


3. A lyuk szűkítése növeli annak bizonyosságát, hogy a foton hol van középen, de az iránya onnan a jobb oldali észlelőernyő felé ennek megfelelően bizonytalanabbá válik. A fókusz elmosódik. A lyuk kiszélesítésével a fotonok mind a detektáló képernyő közepén kötnek ki, de ekkor kevésbé tudjuk, hogy hol voltak, amikor áthaladtak a középső akadályon.


1. A fotonok, elektronok és más szubatomi részecskék egy nagy lyukon átlőve éles fókuszba kerülnek, de nem tudjuk, hogy pontosan hol voltak útjuk közepén.


2. A lyuk szűkítése meggörbíti a részecskék útját a lyuk szélei körül (diffrakció), így a keletkező sugár nagyobb és lágyabb lesz.

Hogyan tanult az ember a bizonytalanságról?

Nagyon röviddel azután, hogy Werner Heisenberg megalkotta az új kvantumfizikát, valami váratlanul jött ki a matematikából, ez a kifejezés:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad \qquad }

A pozíció (x) hiba tartománya szorozva az impulzus (p) hiba tartományával körülbelül egyenlő vagy nagyobb, mint a Planck-állandó osztva 4π-vel.

Ezek a szimbólumok matematikai formába öntik azt, amit a fenti képeken már láttál. A szimbólumok világosan kimondják, hogy nem lehetünk tökéletesen biztosak abban, hogy valami hol van és hová tart. Ha bármikor tisztábban látod, hogy hol van, akkor kevésbé tudod, hogy merre és milyen gyorsan halad. Ha bármikor tisztábban látod, hogy merre megy és milyen gyorsan, akkor kevésbé tudod, hogy hol van most.

A tudósok már megtudták, hogy bizonyos anyagok miért bocsátanak ki jellegzetes fényszíneket, amikor felmelegítik vagy más módon gerjesztik őket. Heisenberg megpróbálta megmagyarázni, hogy miért van ezeknek a színeknek egy-egy jellegzetes fényereje. Nem lett volna elég, ha ő és a többi tudós csak annyit mondott volna: "Hát, ez már csak így van". Biztosak voltak abban, hogy jó oknak kell lennie ezeknek a különbségeknek, és annak a ténynek, hogy a fényes vonalak erősségei közötti arányok egy elem minden egyes mintájánál mindig azonosak.

Nem is sejtette, hogy a természet rejtett titkára bukkan, amikor elindult, hogy felfedezze az egyes elemekre jellemző színes vonalak intenzitásának magyarázatát. A kvantummechanika tanulmányozása már megmutatta, hogy a hidrogénnek miért van négy fényes vonala a spektrum ember által látható részén. Úgy tűnhetett, hogy a következő dolog, amit meg kell tanulni, egyszerűen az lesz, hogyan lehet kiszámítani a fényességüket. A hidrogén tűnt a legkézenfekvőbb kiindulópontnak, mivel a hidrogénnek csak egy elektronja van, és csak négy vonala a spektrum látható részén. Bizonyára jó oka van annak, hogy nem egyformán fényesek. A neon és a többi elem eltérő színű vonalainak fényességére adott magyarázat várhatott.

 

Heisenberg a kvantumfizikán úgy kezdett el dolgozni, hogy az elektromosság klasszikus egyenleteit adaptálta, amelyek eleve nagyon bonyolultak, így az 1925-ös tanulmánya mögött álló matematika nagyon nehezen volt követhető.

Megpróbálta megtalálni a megfelelő módszert a hidrogénlámpa spektrumában lévő fényes vonalak intenzitásának kiszámítására. Meg kellett találnia egy "amplitúdó" nevű kapcsolódó mennyiséget, és az amplitúdót meg kellett szoroznia az amplitúdóval (vagy más szóval négyzetre kellett szoroznia az amplitúdót), hogy megkapja a kívánt intenzitást. Ki kellett találnia, hogyan fejezze ki az amplitúdót úgy, hogy figyelembe vegye azt a tényt, hogy a hidrogénlámpák nem minden frekvencián sugároznak, és nem a spektrum ember által látható részén nem egy folyamatos frekvenciatartományban sugároznak. Heisenberg az amplitúdó kiszámításának egy figyelemre méltó új módját találta meg.

A furcsa egyenletet|egyenletet, amelyet Heisenberg felfedezett és használt egy kvantummennyiség (pl. pozíció) és egy másik (pl. impulzus) szorzására, a "Heisenberg 1925. júliusi "mágikus" dolgozatának" nevezett műben publikálta.

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\,A(n,n-a)B(n-a,n-b)}

A fenti matematika nagyon nehéznek tűnik, de a hozzá vezető matematika sokkal nehezebb, és rendkívül nehéz megérteni. Itt csak azért adjuk meg, hogy megmutassuk, hogyan nézett ki. Heisenberg tanulmánya történelmi mérföldkő. Sok fizikus, aki elolvasta a dolgozatát, azt mondta, hogy nem tudtak egyetérteni a következtetéseivel, de nem tudták követni a magyarázatát, hogy hogyan jutott el ezekhez a következtetésekhez. A Heisenberg által használt kezdőegyenletek Fourier-sorozatokat tartalmaztak, és sok tényezőt tartalmaztak. Visszatérünk a fenti egyenletre, mert ez egyfajta recept a mátrixok kiírásához és szorzásához.

Az új egyenleteknek azért kellett ilyen furcsának és szokatlannak lenniük, mert Heisenberg egy olyan furcsa világot írt le, amelyben bizonyos dolgok, például az elektronok pályái, lassan nem válnak kisebbé vagy nagyobbá. Az újfajta változások ugrásokkal és az ugrások közötti nagy hézagokkal járnak. Az elektronok csak bizonyos pályák között tudnak ugrálni, és a pályák közötti váltás során nyert vagy elveszített energia akkor keletkezik, amikor egy megfelelő energiájú fotont elnyelnek, vagy egy új, megfelelő energiájú foton keletkezik. Ha a hidrogénatomokban az elektronok leggyakrabban két adott pálya között ugranak le (esnek), akkor azon az energiaszinten több foton fog kisugárzódni, és így az ezen a szinten keletkező fény lesz a legintenzívebb.

Nehéz volt a folytonos spektrumokra (amit akkor látunk, amikor a napfényt egy prizmán keresztül engedjük) épített egyenleteket olyan spektrumokra illeszteni, amelyeknek csak néhány csúcsfrekvenciája van, amelyek között nincs semmi. Szinte mindent, amit a fényről és az energiáról már megtanultunk, nagy dolgokkal, például égő gyertyákkal vagy napokkal végeztük, és ezek a nagy tárgyak mind folytonos spektrumot produkálnak. Bár ezekkel a közönséges méretű dolgokkal könnyű volt kísérleteket végezni, mégis hosszú időbe telt, mire rájöttek az őket irányító (fizikai)törvényszerűségekre. Most a fizikusok olyan dolgokkal foglalkoztak, amelyek túl kicsik voltak ahhoz, hogy lássák őket, olyan dolgokkal, amelyek nem produkáltak folytonos spektrumot, és megpróbálták megtalálni a módját annak, hogy legalább olyan támpontokat kapjanak abból, amit már tudtak, ami segíthet nekik megtalálni ezeknek a kicsi és hézagos fényforrásoknak a törvényeit.

Az eredeti egyenletek egyfajta rezgő testtel foglalkoztak, amely egy hullámot hoz létre, kicsit úgy, mint ahogyan egy orgonában a nád egy jellegzetes frekvenciájú hanghullámot hoz létre. Tehát volt egy előre-hátra mozgás (mint a nád rezgése), és volt egy kibocsátott hullám, amelyet szinuszhullámként lehetett ábrázolni. Az atomi szintű fizikáról korábban kitalált dolgok nagy része az atommagok körül mozgó elektronokhoz kapcsolódott. Amikor egy tömeg egy pályán mozog, amikor valamilyen csomópont körül forog, akkor van egy úgynevezett "szögnyomatéka". A szögnyomaték az a mód, ahogyan valami, például egy körhinta tovább forog, miután az emberek már nem tolják. A fázisszámításokhoz és a szögnyomatékhoz használt matematika bonyolult. Ráadásul Heisenberg nem mutatta be az összes számítását az 1925-ös tanulmányában, így még a jó matematikusoknak is gondot okozhat kitölteni azt, amit nem mondott el.

Bár sok fizikus azt mondta, hogy nem tudta megfejteni a Heisenberg áttörést hozó tanulmányának különböző matematikai lépéseit, egy nemrég megjelent cikk, amely megpróbálja megmagyarázni, hogyan jutott Heisenberg az eredményéhez, húsz matematikával teli oldalt használ. Még ez a cikk sem könnyen érthető. A matematika nagyon nehéz dolgokkal kezdődött, és végül valami viszonylag egyszerűt eredményezne, ami a cikk tetején látható. Az egyszerűbb eredmény elérése nem volt egyszerű, és nem is próbáljuk meg bemutatni azt a folyamatot, ahogyan az univerzumról alkotott elavult képtől eljutunk az új kvantumfizikáig. Csak annyi részletre van szükségünk, hogy megmutassuk, hogy szinte azonnal, amint Heisenberg áttörést ért el, a világegyetem működésének egy olyan része került a látókörünkbe, amelyet korábban senki sem látott.

Heisenberg nagyon izgatott lehetett, de nagyon fáradt is, amikor késő este végre áttörést ért el, és elkezdte bizonyítani magának, hogy ez működni fog. Szinte azonnal észrevett valami furcsát, valami olyasmit, amiről azt gondolta, hogy egy bosszantó kis probléma, amit valahogy el tudna tüntetni. De kiderült, hogy ez a kis kellemetlenség egy nagy felfedezés volt.

Heisenberg az amplitúdók amplitúdókkal való szorzása felé haladt, és most Heisenbergnek volt egy jó módja arra, hogy az amplitúdót az új egyenletével kifejezze. Természetesen a szorzáson gondolkodott, és azon, hogyan szorozhatna meg olyan dolgokat, amelyeket bonyolult egyenletekkel adtak meg.

Heisenberg rájött, hogy az amplitúdó négyzetre szorzása mellett előbb-utóbb a pozíciót is meg akarja szorozni az impulzussal, vagy az energiát az idővel, és úgy tűnt, hogy nem lesz mindegy, ha ezekben az új esetekben megfordítja a sorrendet. Heisenberg úgy gondolta, hogy nem számít, hogy a pozíciót szorozzuk-e az impulzussal, vagy az impulzust szorozzuk a pozícióval. Ha ezek csak egyszerű számok lettek volna, akkor nem lett volna probléma. De mindkettő bonyolult egyenlet volt, és az, hogy hogyan kaptad meg a számokat az egyenletekbe illesztve, különbözőnek bizonyult attól függően, hogy melyik úton indultál el. A természetben meg kellett mérni a pozíciót, majd a lendületet, vagy pedig meg kellett mérni a lendületet, majd a pozíciót, és a matematikában ugyanez az általános helyzet érvényesült. (Lásd az angol Wikipédia Heisenberg belépője a mátrixmechanikába című cikkét, ha kíváncsi vagy a kényes részletekre!) Az eredmények közötti apró, de bosszantó különbségek megmaradtak, bármennyire is kívánta Heisenberg, hogy eltűnjenek.

Heisenberg akkoriban nem tudott megszabadulni ettől az egy kis problémától, de kimerült volt, ezért leadta a munkáját közvetlen felettesének, Max Bornnak, és szabadságra ment.

Max Born figyelemre méltó matematikus volt, aki hamarosan rájött, hogy a Heisenberg által adott egyenlet egyfajta recept egy mátrix megírására. Dr. Born azon kevesek egyike volt abban az időben, akiket érdekelt ez a furcsa matematika, amelyről a legtöbben úgy gondolták, hogy nem sok mindenre jó. Tudta, hogy a mátrixokat meg lehet szorozni, így az összes számítást elvégezve egy fizikai probléma elszámolásához úgy lehetett megoldani, hogy az egyik mátrixot megszorozták egy másikkal. Már az is megkönnyítené a munkát, ha egy bonyolult eljárást szabványos és elfogadható formába tudna önteni. Talán mások számára is könnyebben elfogadhatóvá tenné.

Born olyan jó matematikus volt, hogy szinte azonnal rájött, hogy a két mátrix szorzási sorrendjének megváltoztatása más eredményt ad, és az eredmények kis mértékben különböznek egymástól. Ez az összeg h/2πi lenne. A mindennapi életben ez a különbség olyan kicsi lenne, hogy észre sem vennénk.

Két, egymással fázison kívüli hullám


Neon spektrum


A Nap teljes vizuális spektruma. Nincsenek hézagok. Ez a diagram a különböző frekvenciák intenzitását mutatja.


Amikor bizonyos molekulák gerjesztődnek, jellegzetes színt bocsátanak ki.


Hidrogén spektrum

A bizonytalanság formális elméletéhez

Néhány évbe telt, de Heisenbergnek sikerült bebizonyítania a Bizonytalansági Elvet, amely szerint Δx × Δp = h/2, ami az eredeti egyenletekből kikerülő szám, de kihagyja a π-t és az i-t, amelyek a fázisváltozásokkal kapcsolatosak. Heisenberg kifejtette, hogy a bizonytalansági elvét ebből a korábbi eredményből vezette le, amikor 1927-ben írt egy tanulmányt, amelyben bemutatta ezt az elméletet.

A h-val írt állandó, amit Planck-állandónak neveznek, egy rejtélyes, gyakran előforduló szám, ezért meg kell értenünk, hogy mi ez az apró szám. Számszerűen általában 6,62607×10^-34 J s (joule másodperc) értékkel szokták megadni. Tehát ez egy olyan mennyiség, amely magában foglalja az energiát és az időt.

Akkor fedezték fel, amikor Planck felismerte, hogy egy tökéletes sugárzó (úgynevezett fekete test sugárzó) energiája meghatározott méretű egységekben, úgynevezett "kvantumokban" (e szó egyes számban "kvantum") bocsátódik ki. A kisugárzott energia fotonok formájában kerül kibocsátásra, és egy foton frekvenciája arányos az általa leadott "ütéssel". A látható fény különböző frekvenciáit különböző színekként érzékeljük. A spektrum ibolyántúli végén minden egyes foton viszonylag nagy energiával rendelkezik; a spektrum vörös végén minden egyes foton viszonylag kis energiával rendelkezik. A foton energiájának kiszámítására az E = hν egyenlet szolgál (az energia egyenlő a Planck-állandó és a "nu" vagy frekvencia szorzatával).

A Heisenberg-féle bizonytalansági elv Δx × Δp ≥ h azt mondja, hogy amikor bizonyos számpárokat próbálunk meghatározni, csak olyan közel tudunk kerülni hozzájuk, hogy ha az egyiket megpróbáljuk tisztázni, vagyis ha megpróbáljuk Δx-et kisebbre venni, hogy jobban tudjuk valaminek a helyzetét, akkor a számpár másik számához egy nagyobb számot kell visszakapnunk, és hogy a kettő közötti eltérés szorosan összefügg h-val.

Egy másik fizikai mennyiségpár a bizonytalansági összefüggés szerint megy: ΔE × Δt ≥ h, és ez a páros többek között azt jelzi, hogy ha a csillagközi térben nézzük, valami olyan helyen, ahol egyáltalán nem várnánk, hogy bármit is találjunk, és Δt-t egyre közelebb és közelebb csökkentjük 0-hoz, akkor az egyenletben mutatott egyensúly megtartásához ΔE-nek egyre nagyobbnak kell lennie - és hirtelen valami lendületes dolog bukkanhat fel, csak arra a rövid időre.

Hogyan magyarázható ez a meghatározatlanság (a bizonyosság hiánya)? Mi történik az Univerzumban? Gyakran mondják, hogy egy sikeres új elmélet új információkkal szolgálhat a vizsgált jelenségekről. Heisenberg olyan matematikai modellt alkotott, amely megjósolta a hidrogén fényes vonalú spektrumának helyes intenzitásait, de anélkül, hogy ezt szándékosan tette volna, felfedezte, hogy bizonyos fizikai mennyiségpárok váratlan bizonytalanságot tárnak fel. Addig a pillanatig senkinek sem volt fogalma arról, hogy a méréseket nem lehet örökké egyre pontosabbá és pontosabbá tenni. Az a tény, hogy nem lehet őket még biztosabbá, még határozottabbá tenni, megdöbbentő új felfedezés volt. Sokan nem voltak hajlandók elfogadni.

Bohr és kollégái azt állították, hogy a fotonoknak, elektronoknak stb. nincs sem pozíciójuk, sem impulzusuk, amíg nem mérik őket. Ez az elméleti álláspont a bizonytalanság felfedezéséből nőtt ki, és nem csak valami személyes preferencia volt, hogy mit higgyünk. Bohr azt mondta, hogy semmit sem tudunk valamiről, például egy fotonról vagy elektronról, amíg meg nem figyeljük. Ahhoz, hogy egy ilyen kis dolgot megfigyelhessünk, valahogy kölcsönhatásba kell lépnünk vele. A mindennapi életben olyasmit lehet tenni, mint például egy autó mellett sétálni, miközben feljegyezzük, hogy az autó mikor halad át a járdára rajzolt rácson. Talán maga az autó súlya nyomja le a járdában lévő kis karokat, amelyek kikapcsolják az egyes karokhoz rögzített órákat, és feljegyzik az autó súlyát. A végén világos feljegyzést kapnánk arról, hogy az autó hol tartózkodik a különböző időpontokban, és ki tudnánk számítani a haladási irányát és a súlyát is. Így az óra bármelyik időpontjában tudnánk mind a helyzetét, mind a lendületét (a sebességét és a tömegét szorozva). Még csak nem is gondolnánk, hogy a kis karok mozgatásához szükséges erőnek bármilyen hatása lenne az autó haladására. Azt sem képzelnénk, hogy az autónak nincs helyzete vagy pályája a járda azon pontjai között, ahol a karok vannak, vagy hogy az autó ezekben az időkben egyfajta háromdimenziós homályban létezik, és csak akkor helyezkedik el, amikor lenyom egy kart. Az általunk ismert világ nem tárja fel ezeket a furcsa kölcsönhatásokat.

Ahhoz, hogy a legsötétebb éjszakában egy hajót megtaláljunk a tengeren, használhatunk keresőfényt, és ez a fény nem zavarja meg a hajó helyzetét vagy haladási irányát, de egy elektron fény segítségével történő helymeghatározásához egy vagy több fotonnal kellene eltalálni, amelyek mindegyike elég impulzussal rendelkezik ahhoz, hogy megzavarja az elektron helyzetét és röppályáját. Az elektron más eszközökkel történő lokalizálása azt jelentené, hogy az elektront valamilyen fizikai korlátok közé kellene szorítani, ami szintén megszakítaná az előrehaladását.

Egy foton lokalizálása érdekében a legjobb, amit az előrehaladó mozgásának megszakítása nélkül megtehetünk, hogy egy akadályon lévő kör alakú lyukon keresztül vezetjük. Ha ismerjük a foton kibocsátásának időpontját (például egy lézer által) és azt az időpontot, amikor a foton megérkezik egy érzékelő képernyőre, például egy digitális kamerára, akkor kiszámítható, hogy mennyi idő alatt tette meg ezt a távolságot, és hogy a foton mikor haladt át a lyukon. Ahhoz azonban, hogy a foton áthaladhasson rajta, a kör alakú lyuk átmérőjének nagyobbnak kell lennie, mint a foton mérete. Minél kisebb a kör alakú lyuk, annál közelebb kerülünk ahhoz, hogy megismerjük a foton pontos helyzetét, amint áthalad rajta. Azt azonban soha nem tudhatjuk meg, hogy a foton ekkor nem középen van-e. Ha a lyuk pontosan akkora, mint a foton, akkor nem fog átmenni rajta. Ahogy a lyuk átmérője csökken, úgy változik meg egyre nagyobb mértékben a foton lendülete vagy iránya, ahogy elhagyja a lyukat.

Niels Bohr és kollégái azt állították, hogy nagy bajba kerülünk, ha a mikroszkóppal sem látható, túl kicsi dolgokról bármit is igaznak feltételezünk, amire csak a mindennapi élet léptékében van bizonyítékunk. A mindennapi életben a dolgoknak mindenkor meghatározott helyük van. Az atomi léptékben nincs bizonyítékunk arra, hogy ezt a következtetést alátámasszuk. A mindennapi életben a dolgoknak meghatározott időpontjuk van, amikor bekövetkeznek. Az atomi skálán nincs bizonyítékunk arra, hogy ezt a következtetést alátámasszuk. A mindennapi életben, ha valaki megfigyel egy gyárat az első nap éjszakai műszakjától a második nap nappali műszakjáig, és lát egy kész autót kigurulni a rakodódokkba, akkor semmi értelme nem lenne azt mondani, hogy lehetetlen megmondani, hogy az éjszakai műszakban vagy a nappali műszakban szállították-e le. De az atomi léptékben tudunk olyan eseteket mutatni, amikor egyetlen fotont úgy kell számolnunk, mintha két időpontban keletkezett volna. (Ha ez nem lenne elég rossz, olyan eseteket is meg tudunk mutatni, amikor egyetlen foton két szomszédos lézerrel keletkezik).

Az atomi léptékben zajló folyamatok kiderítésének nehézsége részben abban áll, hogy szeretnénk tudni, hol van valami, és mi a pályája, és mindkettőt egyszerre szeretnénk tudni, de nem tudjuk egyszerre mérni a helyzetet és a pályát. Vagy egyszerre mérjük meg egy foton vagy elektron impulzusát, majd a szükségesnél nagyobb késedelem nélkül megmérjük a helyzetét, vagy megcseréljük a dolgokat, és először a helyzetet, majd az impulzust mérjük. A probléma az, hogy azzal, hogy az elsőt eléggé határozott formába hozzuk (valamilyen módon leszorítjuk), növeljük a következő méréssel járó bizonytalanságot. Ha a kezdeti méréseink olyan durvák lennének, hogy mindegyikbe sok hiba kerülne, akkor javíthatnánk a dolgokon azzal, hogy minden egyes mérésnél könnyedebb tapintással végeznénk, de soha nem jutnánk túl egy bizonyos pontossági határon.

A mindennapi életből tudjuk, hogy a mosógépre helyezett fürdőszobai mérlegen a centrifugálási ciklusban történő mérlegelés pontatlan eredményt ad, mert a mérleg tűje csúnyán megremeg. Kikapcsolhatjuk a mosógépet. A nagyon pontos mérésekhez azonban azt tapasztaljuk, hogy a környéken elhaladó teherautók is rázzák a tűt, ezért a mérleget ráhelyezhetjük valamire, hogy elszigeteljük a külső zavaroktól. Úgy gondoljuk, hogy a rezgéseket eléggé ki tudjuk küszöbölni ahhoz, hogy olyan pontos eredményeket kapjunk, amilyeneket szeretnénk. Soha nem gondolunk arra, hogy a mérlegen lévő dolog maga is rezeg, vagy hogy meghatározhatatlan lendülettel rendelkezik.

A Bizonytalansági Elvből visszafelé érvelve úgy tűnik, hogy valójában nincs határozott pozíció és nincs határozott impulzus semmilyen atomi méretű dolog számára, és hogy a kísérletezők csak a Bizonytalansági Elv által meghatározott határon belül kényszeríthetik a dolgokat a határozottságra. Bohr és kollégái csak azzal érveltek, hogy mérések nélkül semmit sem tudhatunk, és ha méréseket végeztünk, akkor a dolgokat a határozottabb pozíció vagy a határozottabb impulzus irányába tudjuk terelni, de nem kaphatunk olyan abszolút meghatározottságot vagy bizonyosságot, amilyet szeretnénk. Mások azonban komolyan vették ezt a lehetőséget, és azzal érveltek, hogy ha a matematika helyes, akkor az ultrakicsinyek világában nem lehet meghatározottság vagy bizonyosság. A tudomány természetéből adódik, hogy a matematika csak a valóság modellje, és nincs garancia arra, hogy ez a modell helyes.

A matematika és a matematika által megjósolt dolgok gyakorlati következményei annyira megbízhatóak, hogy nagyon nehéz velük nem egyetérteni, de amit a matematika a való világról mond, az számos különböző elképzelést eredményezett. A Niels Bohrral Koppenhágában együtt dolgozó tudósok körében a bizonytalansági elvet úgy értelmezték, hogy elemi szinten a fizikai világegyetem nem determinisztikus formában létezik. Inkább valószínűségek vagy lehetőségek gyűjteménye.

A koppenhágai csoport által a matematika köré szőtt történettel szemben vannak más történetek is, mint például a "többszörös univerzum értelmezés", amely szerint minden alkalommal, amikor a kvantumelmélet szerint több lehetséges kimenetel van, minden kimenetel egy saját új univerzumban történik. Einstein azzal érvelt, hogy nincs több lehetséges kimenetel, tehát csak egy univerzum létezik, és az determinált, vagy ahogy ő fogalmazott: "Isten nem kockázik".

Ha h lenne a lehető legkisebb energiamennyiség, akkor a különböző frekvenciájú fotonokban lévő energiát mutató alapegyenlet nem lenne egyensúlyban. Téves lenne.

Ellenvetések a bizonytalansági elvvel szemben

Albert Einstein úgy látta, hogy az új kvantummechanika a mérések előtti időben a pozíció és a lendület hiányát feltételezi, és határozottan tiltakozott ellene. Határozottan hitt abban, hogy a dolgoknak a mérés előtt határozott helyzete és határozott impulzusa volt, és hogy az a tény, hogy egy pár dologból az egyiket megmérve megzavarja a másik pontos mérésének lehetőségét, nem érvel amellett, hogy ezek közül bármelyiknek a hiánya előzetesen fennállt. Ő és két kollégája megírta az "EPR-papír" néven ismertté vált dolgozatot. Ez a papír azt állítja, hogy létezniük kell olyan tulajdonságoknak, amelyek valóban meghatározzák a pozíciót és a lendületet, és ha ezeket látnánk, vagy ha információt kaphatnánk róluk, akkor matematikailag megismerhetnénk és megjósolhatnánk a pozíciót és a lendületet. Az emberek sokáig úgy gondolták, hogy nem lehet bizonyítani vagy cáfolni azt, ami Einstein számára hitcikk volt. A vita nagyon termékeny volt, mert ez vezetett az összefonódással kapcsolatos összes modern fejlesztéshez.

Matematikailag Einstein tévedését bizonyították. 1964-ben John Stewart Bell kifejlesztett egy matematikai módszert, amellyel különbséget lehet tenni két olyan részecske viselkedése között, amelyek állapota determinált, és csupán a két őket vizsgáló személy számára ismeretlen, illetve két olyan részecske viselkedése között, amelyek állapota összefonódott, és amelyek állapota meghatározatlan vagy bizonytalan, amíg meg nem mérik őket. Módszere megmutatja, hogy a két különböző feltevés esetén eltérőek a valószínűségek arra, hogy bizonyos eredményekhez jussunk. Munkáját Bell-tételnek vagy Bell-egyenlőtlenségnek nevezik. Kísérletek kimutatták, hogy a természet úgy viselkedik, ahogy Bell leírja.

Egy másik út a bizonytalansághoz

A Heisenberg-féle bizonytalansági elv kezdeti vitái egy olyan modelltől függtek, amely nem vette figyelembe, hogy az anyag részecskéinek, például az elektronoknak, protonoknak stb. van hullámhosszuk. Louis de Broglie 1926-ban kimutatta, hogy minden dolognak, nem csak a fotonoknak van saját frekvenciája. A dolgoknak hullám- és részecskejellegük van, ahogyan a fotonoknak is. Ha megpróbálnánk egy olyan dolog hullámát, mint egy proton, keskenyebbé és magasabbá tenni, az egyértelműbbé tenné a helyzetét, de akkor az impulzusa kevésbé lenne jól meghatározható. Ha megpróbáljuk a hullám leírásának impulzus részét egyértelműbbé tenni, azaz szűkebb értéktartományban tartani, akkor a hullámcsúcs szétterül, és a helyzete kevésbé lesz határozott.

A foton leírásának részét képező hullám a kvantummechanika szerint nem azonos az óceán felszínén lévő hullámmal, vagy a hanghullámokat alkotó, sűrített levegő és ritka levegő tartományaival. Ehelyett ezeknek a hullámoknak vannak csúcsai vagy nagy amplitúdójú régiói, amelyeknek köze van ahhoz a valószínűséghez, hogy a tér és az idő adott pontján találunk valamit. Pontosabban, az amplitúdó négyzete adja meg valamilyen jelenség megjelenésének valószínűségét.

A fotonra vonatkozó hullám lehet egy tiszta szinuszhullám. Ebben az esetben minden csúcsérték négyzete adná meg annak a valószínűségét, hogy az adott ponton fotont észlelünk. Mivel a szinuszhullámok amplitúdói mindenhol azonosak, a foton megtalálásának valószínűsége minden egyes ponton azonos lenne. Gyakorlatilag tehát az egyik foton hullámának ismerete nem adna támpontot arra vonatkozóan, hogy hol keressük a fotont. Másrészt egy foton impulzusa matematikailag összefügg a hullám amplitúdójával. Mivel ebben az esetben tiszta szinuszhullámmal van dolgunk, a hullám minden ciklusának amplitúdója azonos, ezért ehhez a hullámhoz csak egy impulzusérték tartozik. Nem tudnánk, hogy a foton hol csapódna be, de pontosan tudnánk, hogy milyen erővel csapódna be.

Az érzékelő képernyő egy pontjára fókuszáló fénysugarakban a fotonokhoz kapcsolódó hullámok nem tiszta szinuszhullámok. Ehelyett olyan hullámok, amelyeknek egy ponton nagy az amplitúdója, és a legmagasabb csúcs mindkét oldalán sokkal kisebb amplitúdójúak. Matematikailag lehetséges egy ilyen hullámot több különböző hullámhosszú szinuszhullámra elemezni. Kicsit könnyebb szemléltetni ennek a folyamatnak a fordítottját, ha egy kezdeti, egy frekvenciájú szinuszhullámot nézünk, amelyhez hozzáadunk egy második, más hullámhosszú szinuszhullámot, majd egy harmadikat, majd egy negyediket, és így tovább. Az eredmény egy komplex hullám lesz, amely egy magas csúcsot mutat, és nagyszámú, különböző hullámhosszúságú és ezért különböző impulzusú hullámot tartalmaz. Ebben az esetben rendkívül nagy a valószínűsége annak, hogy a foton egy bizonyos pontban jelenik meg, de az általa szállított impulzusról kiderülhet, hogy az a komponens hullámok bármelyikének hullámhosszával függ össze. Más szóval a p = ħ/λ érték már nem egyetlen érték, mert az összeállított "különböző hullámhosszúságú hullámok" összes hosszát figyelembe kell venni.

A szimuláció megmutatja, hogyan lehet matematikailag modellezni a részecske helyének kiéleződését: Az eredeti szinuszhullám fölé sok különböző hullámformát helyezünk. A középpont egyre magasabb csúcsot fog képezni, a többi csúcsnak pedig megnő a száma, de csökken a magassága, mert interferálnak egymással. Így a végén a szuperpozícióban sok különböző hullám van, mindegyiknek más hullámhossza és (p = ħ/λ szerint) más impulzusa van, de csak egy nagyon magas csúcs, amely egyre magasabbra és keskenyebbre nő, és egyre közelebb ad valamit egy meghatározott helyzethez.

Ahhoz, hogy a lendületet egyre határozottabbá tegyük, egyre többet és többet kellene elvennünk az egymásra helyezett szinuszhullámokból, amíg csak egy egyszerű szinuszhullám marad. Ezáltal fokozatosan csökkentenénk a központi csúcs magasságát, és fokozatosan növelnénk a versengő helyek magasságát, ahol a részecskét megtalálhatjuk.

Amikor tehát a szubatomi részecskék hullámképéből indulunk ki, jellemzően mindig olyan esetekkel fogunk foglalkozni, amelyeknek viszonylag magas a központi csúcsa és viszonylag sok a komponens hullámhossza. Ilyen körülmények között soha nem lesz pontos pozíció vagy pontos impulzus megjósolható. Ha a matematikai modell a valós világ pontos leképezése, akkor egyetlen fotonnak vagy más szubatomi részecskének sincs sem pontos pozíciója, sem határozott impulzusa. Amikor egy ilyen részecskét mérünk, választhatunk olyan módszert, amely tovább szorítja a csúcsot és keskenyebbé teszi, vagy választhatunk olyan módszert, amely csökkenti a csúcsot és kiegyenlíti az összetevők hullámhosszát. Attól függően, hogy mit mérünk és hogyan mérünk, határozottabbá tehetjük a helyünket, vagy szűkíthetjük a lendület tartományát. A kísérlet megtervezésénél ügyelhetünk arra, hogy elkerüljük a különböző módokon való rázkódást, de nem szabadulhatunk meg attól a ténytől, hogy kezdetben semmi sem volt teljesen határozott.

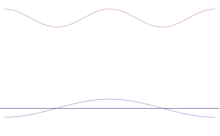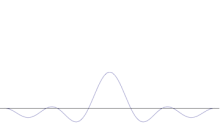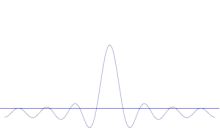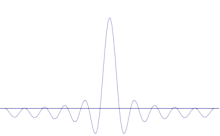
Több síkhullám szuperpozíciója. A hullámcsomag a sok hullám összeadásával egyre inkább lokalizálódik. A Fourier-transzformáció olyan matematikai művelet, amely a hullámcsomagot az egyes síkhullámokra bontja. Megjegyzendő, hogy az itt bemutatott hullámok csak szemléltetés céljából valósak, míg a kvantummechanikában a hullámfüggvény általában komplex.

Kulturális hatások

A Heisenberg-féle határozatlansági elv legfontosabb hatása az akarat szabadságáról szóló érvekre volt. A klasszikus fizika elméletei alapján azzal lehetett érvelni, hogy az ok és okozat törvényei megállíthatatlanok, és hogy ha a világegyetem egy bizonyos módon kezdődött, akkor a jövőben bekövetkező összes anyag és energia kölcsönhatása kiszámítható ebből a kezdeti állapotból. Mivel minden abszolút annak az eredménye, ami előtte volt, érveltek, minden döntés, amelyet egy ember hoz, és minden helyzet, amelybe az ember kerül, az idők kezdete óta előre meg volt határozva. Nincs tehát választásunk abban, hogy mit teszünk.

Az akarat szabadságában hívők azzal érvelnek, hogy a kvantummechanika törvényei nem azt jósolják meg, hogy mi fog történni, hanem csak azt, hogy mi az, aminek nagyobb és mi az, aminek kisebb a valószínűsége. Ezért minden cselekvés véletlenszerű "pénzfeldobások" sorozatának eredménye, és egyetlen döntés sem vezethető vissza szükséges előfeltételek halmazára.

A "kvantumugrás" és a "kvantumugrás" kifejezések a dolgokról való beszéd hétköznapi módjává váltak. Általában az emberek úgy akarnak leírni valamit, mint ami rövid idő alatt bekövetkező hatalmas változást jelent. A kifejezés valójában arra vonatkozik, ahogyan egy elektron viselkedik egy atomban, amikor elnyel egy kívülről érkező fotont, és így az atommag körül egy pályáról egy magasabb pályára ugrik, vagy amikor fotont bocsát ki, és így egy magasabb pályáról egy alacsonyabb pályára esik. Neils Bohr és munkatársai elképzelése az volt, hogy az elektron nem mozog a pályák között, hanem eltűnik az egyik pályáról, és azonnal megjelenik egy másik pályán. A kvantumugrás tehát valójában nem valami világrengető változás, hanem egy hirtelen kis váltás egyik tartományból a másikba.

Amikor az emberek valamilyen szubatomi szintű folyamatot mérnek, és a bizonytalansági elv megnyilvánul, akkor azt mondhatjuk, hogy az emberi tevékenység befolyásolta a mérendő dolgot. Egy olyan mérés elvégzése, amelynek célja, hogy egy részecske helyének pontos meghatározását kapjuk, elkerülhetetlenül befolyásolni fogja annak impulzusát, és bármit is teszünk annak érdekében, hogy a helyzetének mérése után a lehető leghamarabb megmérjük ezt az impulzust, nem lehet nem megváltoztatni annak valószínűségét, hogy milyen impulzust fogunk felfedezni. A bizonytalansági elv tehát magyarázatot adhat a vizsgálók által keltett, a kísérlet vagy megfigyelés eredményét befolyásoló interferenciák bizonyos fajtáira. Nem minden megfigyelői hatás azonban a kvantumhatásoknak vagy a bizonytalansági elvnek köszönhető. A többi "megfigyelői hatás", de nem kvantumbizonytalansági hatás.

A megfigyelői hatások mindenféle olyan dolgot magukban foglalnak, amelyek a mi hétköznapi emberi léptékű eseményeinkben működnek. Ha egy antropológus megpróbál világos képet kapni egy primitív társadalom életéről, de jelenléte felzaklatja a közösséget, amelyet meglátogat, akkor a megfigyelései nagyon félrevezetőek lehetnek. A releváns kölcsönhatások egyike sem történik azonban a kvantummechanika vagy a bizonytalansági elv által leírt szinten.

Néha a "kvantum" szót reklámcélokra használják, hogy valami új és erőteljes dolgot jelezzenek. Például a kis benzinmotorok gyártójának, a Briggs and Strattonnak van egy sor négyhengeres, kis lóerős motorja benzines fűnyírókhoz és hasonló kerti szerszámokhoz, amelyet "Quantum"-nak nevez.

További olvasmányok

• A kvantumelmélet bevezetése, 115. és 158. o.

J.P. McEvoy és Oscar Zarate