Fénysebesség

Példa

Ez a viselkedés eltér a mozgásról alkotott általános elképzeléseinktől, amint azt ez a példa is mutatja:

George a földön áll néhány vasúti sínek (vasút) mellett. Egy vonat száguld el mellette 30 mph (48 km/h) sebességgel. George 90 mph (140 km/h) sebességgel dob egy baseball-labdát a vonat irányába. Tomnak, a vonat utasának van egy olyan eszköze (mint egy radarpisztoly), amellyel a dobási sebességet mérni tudja. Mivel a vonaton van, Tom már 30 mph (48 km/h) sebességgel halad a dobás irányába, így Tom a labda sebességét csak 60 mph (97 km/h) sebességnek méri.

Más szóval, a baseball-labda sebessége, ahogyan azt Tom a vonaton méri, a vonat sebességétől függ.

A fenti példában a vonat a labda sebességének 1/3-ával mozgott, és a vonaton mért labda sebessége a földön mért dobási sebesség 2/3-a volt.

Most ismételd meg a kísérletet úgy, hogy a baseball-labda helyett fényt használsz, vagyis George-nak van egy zseblámpája, ahelyett, hogy baseball-labdát dobna. George-nak és Tomnak is olyan eszközei vannak, amelyekkel a fény sebességét mérhetjük (a baseball-példában használt radarpisztoly helyett).

George a földön áll néhány vasúti sín mellett. Egy vonat száguld el mellette 1/3 fénysebességgel. George egy fénysugarat villant a vonat irányába. George a fény sebességét 186,282 mérföld/másodpercben (299,792 kilométer/másodperc) méri. Tom, a vonat egyik utasa megméri a fénysugár sebességét. Milyen sebességet mér Tom?

Intuitívan azt gondolhatnánk, hogy a vonaton mért zseblámpa fénysebességének 2/3-ának kellene lennie a földön mért sebességnek, ahogy a baseball-labda sebessége is 2/3 volt. Valójában azonban a vonaton mért sebesség a teljes érték, 186,282 mérföld/másodperc (299,792 kilométer/másodperc), nem pedig 124,188 mérföld/másodperc (199,861 kilométer/másodperc).

Lehetetlenül hangzik, de az ember ezt méri. Ennek részben az az oka, hogy a fény energia, amely egészen másképp viselkedik és mozog, mint az anyag vagy a szilárd tárgyak, például egy baseball-labda.

Maxwell egyenletei megjósolták a fény sebességét, és megerősítették Michael Faraday elképzelését, miszerint a fény elektromágneses hullám (az energia mozgásának módja). Ezekből az egyenletekből kiderül, hogy a fénysebesség a szabad tér áteresztőképessége ε0 négyzetgyökének és a szabad tér áteresztőképessége μ0 négyzetgyökének inverzével függ össze:

c = 1 ε 0 μ 0 . {\displaystyle c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}\ . }

Ennek a ténynek az a következménye, hogy semmi sem haladhat gyorsabban a fénysebességnél. Egy másik következmény, hogy a tömeggel rendelkező tárgyak esetében, bármennyi energiát is használunk fel egy tárgy sebességének növelésére, az egyre közelebb és közelebb kerül, de soha nem éri el a fénysebességet. Ezeket a gondolatokat az 1900-as évek elején fedezte fel Albert Einstein, akinek munkássága teljesen megváltoztatta a fényről alkotott képünket.

Egy tiszta anyag törésmutatója a vákuumban lévő fénysebesség és az adott anyagban lévő fénysebesség aránya.

Mérés

Rømer

Ole Christensen Rømer egy csillagászati mérés segítségével elvégezte a fénysebesség első kvantitatív becslését. A Földről mérve egy távoli bolygó körül keringő holdak periódusa rövidebb, amikor a Föld közeledik a bolygóhoz, mint amikor a Föld távolodik tőle. A fény által a bolygóról (vagy holdjáról) a Földig megtett távolság rövidebb, amikor a Föld a pályájának a bolygóhoz legközelebbi pontján van, mint amikor a Föld a pályájának legtávolabbi pontján van; a távolságkülönbség a Föld Nap körüli pályájának átmérője. A Hold keringési idejének megfigyelt változása valójában a fénynek a rövidebb vagy hosszabb távolság megtételéhez szükséges idő különbsége. Rømer ezt a hatást a Jupiter legbelső holdján, az Io-nál figyelte meg, és arra a következtetésre jutott, hogy a fénynek 22 percbe telik, amíg a Föld pályájának átmérőjét átlépi.

Bradley

Egy másik módszer a fény aberrációjának felhasználása, amelyet James Bradley fedezett fel és magyarázott meg a 18. században. Ez a hatás egy távoli forrásból (például csillagból) érkező fény sebességének és a megfigyelő sebességének vektoriális összeadásából adódik (lásd a jobb oldali ábrát). A mozgó megfigyelő így a fényt kissé más irányból érkezőnek látja, és következésképpen a forrást az eredeti helyzetéhez képest eltolt pozícióban látja. Mivel a Föld sebességének iránya folyamatosan változik, ahogy a Föld kering a Nap körül, ez a hatás a csillagok látszólagos helyzetének elmozdulását okozza. A csillagok helyzetének szögeltéréséből a fénysebesség kifejezhető a Föld Nap körüli sebességével. Ez az ismert évhosszúsággal könnyen átszámítható a Naptól a Földig tartó út megtételéhez szükséges időre. Bradley 1729-ben ezzel a módszerrel kiszámította, hogy a fény 10 210-szer gyorsabban halad a Föld körüli pályán (a mai szám 10 066-szor gyorsabb), vagy ennek megfelelően a fénynek 8 perc 12 másodperc alatt kell eljutnia a Naptól a Földig.

Modern

Manapság a "fényidő egységnyi távolságra" - a c fordítottja (1/c), csillagászati egységenként másodpercekben kifejezve - úgy mérhető, hogy összehasonlítjuk a rádiójeleknek a Naprendszerben lévő különböző űreszközökhöz való eljutási idejét. Az űreszközök helyzetét a Nap és a különböző bolygók gravitációs hatásaiból számítják ki. Sok ilyen mérés kombinálásával kapjuk meg a távolságegységre vetített fényidő legjobban illeszkedő értékét. A Nemzetközi Csillagászati Unió (IAU) által jóváhagyott legjobb becslés 2009-ben^{[frissítés]} a következő:

fényidő egységnyi távolságra: 499.004783836(10) s

c = 0,00200398880410(4) AU/s

c = 173,144632674(3) AU/nap.

E mérések relatív bizonytalansága 0,02 rész/milliárd (2×10-11), ami megegyezik az interferometriával végzett földi hosszmérések bizonytalanságával. Mivel a métert a fény által egy bizonyos időintervallumban megtett hosszként határozzák meg, az egységnyi távolságra eső fényidő mérése úgy is értelmezhető, mint egy AU hosszának mérése méterben. A métert a saját hosszúság mértékegységének tekintik, míg az AU-t gyakran az adott vonatkoztatási rendszerben megfigyelt hosszúság mértékegységeként használják.

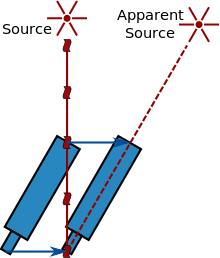
A fény aberrációja: a fény véges sebessége miatt egy távoli forrásból származó fény egy mozgó távcső számára más helyről származónak tűnik.

Gyakorlati hatások

A fény véges sebessége a hosszú távú űrutazás egyik fő korlátja. Ha feltételezzük, hogy a Tejútrendszer túlsó oldalára utazunk, akkor egy üzenet és a válasz teljes időtartama körülbelül 200 000 év lenne. Még ennél is komolyabb, hogy egyetlen űrhajó sem tudna a fénynél gyorsabban utazni, így minden galaktikus méretű közlekedés gyakorlatilag egyirányú lenne, és sokkal tovább tartana, mint ameddig bármely modern civilizáció létezett.

A fény sebessége nagyon rövid távolságokon is aggodalomra adhat okot. A szuperszámítógépekben a fénysebesség korlátot szab annak, hogy milyen gyorsan lehet adatokat küldeni a processzorok között. Ha egy processzor 1 gigahertzes sebességgel működik, egy jel egyetlen ciklus alatt legfeljebb 30 centimétert tud megtenni. A processzorokat ezért közel kell elhelyezni egymáshoz a kommunikációs késleltetések minimalizálása érdekében; ez nehézségeket okozhat a hűtésnél. Ha az órajelfrekvenciák tovább nőnek, a fénysebesség végül korlátozó tényezővé válik az egyes chipek belső kialakításában.

Kapcsolódó oldalak

• Michelson-Morley kísérlet