Logarléc (számológép): működés, típusok és története
Ismerje meg a logarléc (számológép) működését, típusait és történetét: skálák, alkalmazások és fejlődés Napier-től a zsebszámológépig.
A számológép vagy slipstick egy mechanikus analóg számítógép. A számológépet főként szorzásra és osztásra, valamint "tudományos" függvényekre, például gyökszámításra, logaritmusokra és trigonometriára használják, de általában nem összeadásra vagy kivonásra.
A tolószabályoknak sokféle stílusa létezik. Ezek általában lineárisak vagy kör alakúak. Szabványos jelölésekkel (úgynevezett skálákkal) rendelkeznek. Ezeket a skálákat matematikai számításokhoz használják. Egyes számológörbék speciális felhasználásra készültek, például a repüléshez vagy a pénzügyekhez. Ezeknek a szabályozóknak a normál skálák mellett speciális skálái is vannak az ilyen alkalmazásokhoz.
William Oughtred és mások az 1600-as években fejlesztették ki a számológépet. A számológép John Napier logaritmusokkal kapcsolatos munkáján alapul. Az elektronikus számológépek kifejlesztése előtt a tudományos és mérnöki munkában leggyakrabban használt eszköz a számológép volt. A számológépek használata az 1950-es és 1960-as években tovább nőtt, még akkor is, amikor fokozatosan megjelentek a digitális számítástechnikai eszközök; 1974 körül azonban a zsebszámológép nagyrészt elavulttá tette a számológépet, és a legtöbb beszállító kivonult az üzletből.
Működés
A számológép lényege, hogy a számokat logaritmikus skálán ábrázolja: a skála hossza arányos a szám(log) értékével. Szorzásnál két szám logaritmusát egymás mellé helyezve a fizikai távolságok összeadásával kapjuk meg az eredmény logaritmusát, így a tényleges számot a megfelelő skála leolvasásával állapítjuk meg. Osztásnál az egyik skálát az osztóhoz igazítjuk, és a leolvasott helyen olvassuk le a hányadost.
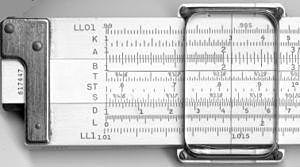
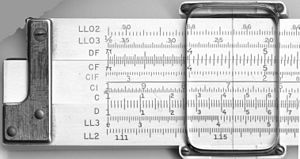
A pontos leolvasást egy mozgatható áttetsző jelölő (a hajvonal vagy cursor) segíti. A számológépen többféle skála található, például C és D (alapskálák szorzás-osztáshoz), A és B (négyzetes skálák), L (logaritmikus skála), S és T (szinusz és tangens skálák) és speciálisabb skálák trigonometriai vagy exponenciális számításokhoz. A használathoz mindig figyelembe kell venni a helyes nagyságrendet (a tizedespont helyét), amit a felhasználó becsléssel vagy kiegészítő jelölésekkel határoz meg.
Típusok és formák
- Lineáris (egyenes) számológépek: a legismertebb változatok, 10–50 cm hosszúak lehetnek; hosszabb szabályok nagyobb pontosságot tesznek lehetővé.
- Kör alakú számológépek: ugyanazt a skálahosszt körkörösen elhelyezve folyamatos skálát adnak, így kompaktabb és gyakran tartósabb megoldást jelentenek.
- Hengeres (cylindrical) számológépek: például Fuller's hengeres szabályai hosszú (többszörös) skálahossz miatt nagyobb pontosságot nyújtanak.
- Speciális műszerek: az E6B repülési számológép, pénzügyi számológépek és mérnöki szabályok speciális skálákkal a navigációhoz, légiforgalomhoz vagy pénzügyi számításokhoz.
Alkatrészek és skálák
Egy tipikus slide rule részei: a test (stock), a középen mozgó slide, valamint a ráhúzható áttetsző cursor. A skálák jelölései szabványosak: C és D a fő szorzó/osztó skálák, CI a C fordítottja, A és B a négyzetre emeléshez, K köbére emeléshez, L a logaritmikus skála, S és T trigonometriai számokhoz. A skálák kombinációja és elrendezése változó lehet gyártótól és felhasználói céltól függően.
Használat és korlátok
Előnyök:
- Gyors, mechanikus számítás szorzásra, osztásra és bizonyos függvényekre.
- Nincs szükség áramra, tartós és mechanikusan egyszerű eszköz.
- Segíti a becslés képességét és a nagyságrendek kezelését.
Korlátok:
- Nem alkalmas közvetlen összeadásra és kivonásra (bár vannak erre kiterjesztett módszerek és speciális skálák).
- A pontosság korlátozott: átlagosan 3–4 érdemi számjegy, hosszabb szabályokkal vagy hengeres megoldásokkal ez 5–6 számjegyig növelhető.
- Felhasználófüggő: a helyes tizedespont-pozíciót mindig a használónak kell megítélnie, így előfordulhatnak emberi hibák.
Történet és fejlődés
A számológép története John Napier logaritmusainak felfedezésére vezethető vissza, amelyek lehetővé tették a szorzás és osztás egyszerűsítését. Ezen alapulva William Oughtred és más feltalálók az 1600-as években hozták létre az első tolószabály-szerű eszközöket. Edmund Gunter munkái a 17. században szintén fontosak voltak (Gunter-skála).
A 19. században a szabványosított skálák és a tömeggyártás elterjedésével a számológépek széles körben elterjedtek a mérnöki és tudományos munkaeszközök között. A 20. század közepén, különösen az 1950–60-as években a számológépek csúcsnépszerűségüket élték, amikor még az elektronikus eszközök ritkák és drágák voltak. A hordozható, olcsó zsebszámológépek megjelenése a 1970-es évekre nagyrészt kiváltotta a tolószabályokat, és az ipar gyakorlatilag eltűnt erről a piacról.
Mai szerep: gyűjtés és oktatás
Bár a mindennapi számításokban mára elavultak, a számológépek ma is fontosak a technikatörténet és a mérnöki gondolkodás oktatásában. Gyűjtők körében értékesek az antik vagy ritka modellek, és a vintage példányok restaurálása népszerű hobbi. Egyes oktatók továbbra is használják a tolószabályt, hogy a diákok jobban megértsék a logaritmusokat, a számskálák működését és a nagyságrendek kezelését.
Gyakorlati tippek
- Mindig kezdjünk becsléssel a tizedespont helyének meghatározásához.
- Használjuk a cursor-t a pontosabb leolvasáshoz és a csúszás minimalizálásához.
- Nagy pontosság kívánalmakor válasszunk hosszabb vagy hengeres számológépet, illetve ellenőrizzük az eredményt egy másik módszerrel is.
- Tartsuk tisztán és szárazon a csúszó felületeket; kerüljük az agresszív tisztítószereket, amelyek károsíthatják a jelöléseket.
Összefoglalva, a számológép nagyszerű példa arra, hogyan használható a logaritmus elve mechanikus eszközben: egyszerű, megbízható és oktatóértéke ma is jelentős, még ha a gyakorlati alkalmazása vissza is szorult az elektronikus számolóeszközök korában.

Egy tipikus tíz hüvelykes diák-tolózár (Pickett N902-T szimplex trigonometria)

Egy tolózár úgy van beállítva, hogy 2-vel szorozzuk. A D (alsó) skálán minden szám a C (középső) skálán a fölötte lévő szám duplája.
Alapfogalmak
Legegyszerűbb formájában a számológép két logaritmikus skálát használ, hogy lehetővé tegye a számok gyors szorzását és osztását. Ezek a gyakori műveletek időigényesek és hibakockázatosak lehetnek, ha papíron végzik őket. A bonyolultabb csúszószabályok más számításokat is lehetővé tesznek, például négyzetgyök, exponenciálisok, logaritmusok és trigonometrikus függvények számítását.
A matematikai számítások úgy történnek, hogy a csúszó középső csíkon lévő jelet összehangoljuk az egyik rögzített csíkon lévővel. Ezután megfigyelhető a többi jel relatív helyzete. A jelekhez igazított számok megadják a szorzat, hányados vagy más számított eredmény hozzávetőleges értékét.
A felhasználó mentális becslés alapján határozza meg a tizedespont helyét az eredményben. A tudományos jelölés a tizedespont követésére szolgál a formálisabb számításokban. Az összeadás és kivonás lépéseit egy számításban általában mentálisan vagy papíron végezzük, nem pedig a számológéppel.
A legtöbb csúszószabály három azonos hosszúságú lineáris csíkkal rendelkezik. A csíkok párhuzamosan vannak elrendezve és egymáshoz illesztve, így a középső csík hosszirányban mozgatható a másik kettőhöz képest. A két szélső csík rögzített, így relatív helyzetük nem változik.
Egyes csúszószabályok ("duplex" modellek) a szabály és a csúszócsík mindkét oldalán, mások a külső csíkok egyik oldalán és a csúszócsík mindkét oldalán, megint mások csak az egyik oldalon ("szimplex" szabályok) rendelkeznek skálákkal. A függőleges igazítóvonallal ellátott csúszó kurzor segítségével megkereshetjük a megfelelő pontokat a skálákon, amelyek nem egymás mellett vannak, vagy a duplex modelleknél a szabály másik oldalán vannak. A kurzor bármelyik skálán egy közbenső eredményt is rögzíthet.

kurzor egy diasoron
A számításhoz egy számológépet használva
Szorzás
A logaritmus a szorzás és osztás műveleteit összeadásra és kivonásra alakítja át a log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} 











A műveletek "túlléphetnek a skálán"; például a fenti ábrán látható, hogy a tolózár a felső skálán lévő 7-et nem helyezte az alsó skála egyik száma fölé sem, így nem ad választ a 2×7-re. Ilyen esetekben a felhasználó a felső skálát balra csúsztathatja, amíg a jobb oldali indexe a 2-vel egy vonalba nem kerül, és így ténylegesen 0,2-vel szorozhat 2 helyett 2-vel, ahogy az alábbi ábrán látható:
![]()
Itt a számológép használójának nem szabad elfelejtenie, hogy a tizedesvesszőt megfelelően állítsa be a végső válasz korrigálásához. Mi 2×7-et akartunk találni, de ehelyett 0,2×7=1,4-et számoltunk. A valódi válasz tehát nem 1,4, hanem 14. A csúszka visszaállítása nem az egyetlen módja az olyan szorzások kezelésének, amelyek a skálától eltérő eredményt adnának, mint például a 2×7; van néhány más módszer is:
- (1) Használja az A és B kétdekás skálákat.
- (2) Használja a hajtogatott mérlegeket. Ebben a példában állítsa a C bal oldali 1-jét a D 2-vel szemben. Vigye a kurzort a CF-en a 7-re, és olvassa le az eredményt a DF-ről.
- (3) Használja a CI inverz skálát. Helyezze a 7-es értéket a CI skálán a D skála 2-es értéke fölé, majd olvassa le az eredményt a D skálán, a CI skála 1-es értéke alatt. Mivel az 1 a CI-skálán két helyen fordul elő, az egyik mindig a skálán lesz.
- (4) Használja mind a CI invertált skálát, mind a C skálát. Állítsuk a CI 2-es értékét a D 1-es értékével egy vonalba, és olvassuk le az eredményt a D-ről, a C skála 7-es értéke alatt.
Az 1. módszer könnyen érthető, de a pontosság csökkenésével jár. A 3. módszer előnye, hogy csak két skálát tartalmaz.
Részleg
Az alábbi ábra az 5,5/2 kiszámítását mutatja be. A felső skálán lévő 2 az alsó skálán lévő 5,5 fölé kerül. A felső skálán lévő 1 a 2,75-ös hányados felett helyezkedik el. Az osztás elvégzésére több módszer is létezik, de az itt bemutatott módszer előnye, hogy a végeredmény nem lehet skálán kívüli, mert az ember választhat, hogy az 1-est bármelyik végén használja.

Egyéb műveletek
A logaritmikus skálák mellett egyes csúszószabályok egyéb matematikai funkciókat is kódolnak más segédskálákon. A legnépszerűbbek a trigonometrikus, általában a szinusz és a tangens, a közönséges logaritmus (log10) (egy érték logaritmusának a szorzós skálán történő felvételére), a természetes logaritmus (ln) és az exponenciális (ex ) skálák voltak. Egyes szabályok közé tartozik a Pitagorasz-skála, a háromszögek oldalainak számításához, és a körök számításához használt skála. Mások skálákat tartalmaznak a hiperbolikus függvények kiszámításához. A lineáris szabályokon a skálák és azok feliratozása nagymértékben szabványosított, eltérés általában csak abban mutatkozik, hogy mely skálák és milyen sorrendben szerepelnek:
| A, B | kétdekás logaritmikus skálák, amelyeket a számok négyzetgyökeinek és négyzeteinek meghatározására használnak. |
| C, D | egy évtizedes logaritmikus skálák |
| K | háromdekás logaritmikus skála, amelyet a számok kockagyökeinek és köbgyökeinek megtalálására használnak. |
| CF, DF | A C és D skálák "hajtogatott" változatai, amelyek az egység helyett π-ről indulnak; ezek két esetben kényelmesek. Először is, amikor a felhasználó úgy sejti, hogy egy termék közel lesz a 10-es értékhez, de nem biztos benne, hogy valamivel kevesebb vagy valamivel több lesz, mint 10, a hajtogatott skálákkal elkerülhető, hogy a skálán kívülre kerüljön. Másodszor, azáltal, hogy a kiindulási érték nem 10 négyzetgyöke, hanem π, a π-vel való szorzás vagy osztás (ahogyan az a természettudományos és mérnöki képletekben szokásos) egyszerűsödik. |
| CI, DI, DIF | "fordított" skálák, jobbról balra haladva, 1/x lépések egyszerűsítésére használva |
| S | szinuszok és koszinuszok meghatározására szolgál a D skálán |
| T | a D- és DI-skálán az érintő és a zárószögek meghatározására szolgál. |
| ST, SRT | kis szögek szinuszaihoz és érintőihez, valamint a fok-árkád átváltáshoz használatos |
| L | lineáris skála, amelyet a C és D skálákkal együtt használnak a 10-es logaritmusok és a 10-es hatványok meghatározására. |
| LLn | log-log skálák készlete, amelyeket a számok logaritmusainak és exponenciálisainak meghatározására használnak. |
| Ln | egy lineáris skála, amelyet a C és D skálákkal együtt a természetes (e bázisú) logaritmusok és az e x {\displaystyle e^{x}} találására használnak. |
| ||
| A K&E 4081-3 tolózár elülső és hátsó skálái. |
A Gilson által 1931-ben gyártott Binary Slide Rule a törtekre korlátozódó összeadás és kivonás funkcióját végezte.
Gyökerek és hatalmak
Vannak egydekás (C és D), kétdekás (A és B) és háromdekás (K) skálák. Az x 2 {\displaystyle x^{2}} kiszámításához 
Az x y {\displaystyle x^{y}}

Trigonometria
Az S, T és ST skálákat trigonometrikus függvényekhez és trigonometrikus függvények többszöröseihez, fokban kifejezett szögekhez használjuk. Sok csúszószabályon az S, T és ST skálák fokokkal és percekkel vannak jelölve. Az úgynevezett decitrig modellek ehelyett a fokok tizedes törtrészeit használják.
Logaritmusok és exponenciálisok
A 10-es bázisú logaritmusokat és exponenciálisokat az L skála segítségével találjuk meg, amely lineáris. Egyes csúszószabályok Ln skálával rendelkeznek, amely az e bázisra vonatkozik.
Az Ln-skálát egy 11. osztályos diák, Stephen B. Cohen találta fel 1958-ban. Az eredeti szándék az volt, hogy a felhasználó az Ln-skálán kiválaszthasson egy x exponenciát (a 0 és 2,3 közötti tartományban), és a C (vagy D) skálán e-tx, a CI (vagy DI) skálán pedig e-t–x olvashasson. A Pickett, Inc. kizárólagos jogokat kapott a skálára. Később a feltaláló létrehozott egy sor "jelet" az Ln skálán, hogy a tartományt a 2,3 határon túlra is kiterjessze, de a Pickett soha nem építette be ezeket a jeleket egyetlen csúszószabályába sem. []
Összeadás és kivonás
A csúszószabályokat általában nem használják összeadásra és kivonásra, de két különböző technikával mégis lehetséges.
Az első módszer az összeadás és kivonás elvégzéséhez a C és D (vagy bármely hasonló skálán) a probléma osztássá alakítását igényli. Összeadásnál a két változó hányadosa plusz az osztó szorzata egyenlő az összegükkel:
x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y}
Kivonás esetén a két változó hányadosa mínusz az osztó szorzata egyenlő a különbségükkel:
x - y = ( x y - 1 ) y {\displaystyle x-y=\left({\frac {x}{y}}-1\right)y}
Ez a módszer hasonlít a logaritmikus számrendszerrel működő nagysebességű elektronikus áramkörökhöz használt összeadási/kivonási technikához, amelyet olyan speciális számítógépes alkalmazásokban alkalmaznak, mint a Gravity Pipe (GRAPE) szuperszámítógép és a rejtett Markov-modellek.
A második módszer egy csúszó lineáris L-skálát használ, amely néhány modellnél elérhető. Az összeadás és kivonás a kurzor balra (kivonás esetén) vagy jobbra (összeadás esetén) történő csúsztatásával történik, majd a csúszkát 0-ra visszavezetve leolvassa az eredményt.
Fizikai kialakítás
Szabványos lineáris szabályok
A tolózár hossza a skálák névleges hosszában van megadva. A leggyakoribb "10 hüvelykes" modellek skálái valójában 25 cm hosszúak, mivel metrikus szabványok szerint készültek, bár egyes szabályok kissé meghosszabbított skálákat kínálnak, hogy egyszerűsítsék a manipulációt, ha egy eredmény túlcsordul. A zsebszabályok jellemzően 5 hüvelykes méretűek. A néhány méter hosszú modelleket azért árulták, hogy tanítási célokra osztálytermekbe akaszthassák őket. [1]
Az osztások általában két számjegy pontosságú skálát jelölnek, a harmadik számjegyet pedig a felhasználó becsüli meg. Egyes csúcskategóriás csúszószabályok nagyító kurzorral rendelkeznek, amely megkönnyíti a jelölések láthatóságát. Az ilyen kurzorok gyakorlatilag megduplázhatják a leolvasások pontosságát, lehetővé téve, hogy egy 10 hüvelykes tolózár ugyanolyan jól használható legyen, mint egy 20 hüvelykes.
Különböző egyéb kényelmi szolgáltatásokat fejlesztettek ki. A trigonometrikus skálákat néha kettős feliratozással látják el, fekete és piros színnel, egymást kiegészítő szögekkel, az úgynevezett "Darmstadti" stílusban. A duplex csúszószabályok gyakran megkettőzik a skálák egy részét a hátoldalon. A skálákat gyakran "osztják" a nagyobb pontosság elérése érdekében.
A mérnöki, üzleti és banki tevékenység különböző formáihoz speciális csúszószabályokat találtak fel. Ezeken gyakran a közös számításokat közvetlenül speciális skálák formájában fejezték ki, például a hitelszámításokat, az optimális beszerzési mennyiségeket vagy bizonyos mérnöki egyenleteket. A Fisher Controls cég például egy olyan egyedi diasort forgalmazott, amely az ipari áramlásszabályozó szelepek megfelelő méretének kiválasztásához használt egyenletek megoldására volt alkalmas. []
Kör alakú tolózárak
A kör alakú csúszószabályoknak két alaptípusa van: az egyik két kurzorral (balra), a másik pedig egy mozgatható tárcsával és egy kurzorral (jobbra). A két kurzoros változatok úgy végzik a szorzást és osztást, hogy a tárcsa körüli forgatás során a kurzorok között állandó szöget tartanak fenn. Az egy kurzoros változat a skálák megfelelő beállítása révén inkább a hagyományos tolózárhoz hasonlóan működik.
A kör alakú tolózár alapvető előnye, hogy a szerszám leghosszabb mérete körülbelül 3-szorosára (azaz π-vel) csökkent. Például egy 10 cm-es körkörös külső skála maximális pontossága megegyezne egy 30 cm-es közönséges tolózárral. A kör alakú tolózárak kiküszöbölik a "skálán kívüli" számításokat is, mivel a skálákat úgy tervezték, hogy "körbeöleljenek"; soha nem kell őket átigazítani, ha az eredmények 1,0 közelében vannak - a vonalzó mindig a skálán van. A nem ciklikus, nem spirális skálák, mint például az S, T és LL skálák esetében azonban a skála hossza megrövidül, hogy helyet biztosítson a szélső margóknak.
A kör alakú tolóbillentyűk mechanikailag robusztusabbak és simábban mozognak, de a skála beállítási pontossága érzékeny a központi tengely centrálására; a tengely 0,1 mm-es eltérése a legrosszabb esetben 0,2 mm-es beállítási hibát eredményezhet. A tengely azonban megakadályozza a mérőfelület és a kurzorok karcolódását. A legnagyobb pontosságú skálák a külső gyűrűkön helyezkednek el. A "osztott" skálák helyett a csúcsminőségű körszabályok spirálskálákat használnak az összetettebb műveletekhez, mint például a logaritmus-alapú skálázások. Az egyik nyolc hüvelykes prémium körszabály 50 hüvelykes spirális log-log skálával rendelkezett.
A kör alakú csúszószabályok fő hátránya, hogy a forgó tárcsa mentén nehezen találhatók meg a számjegyek, és a skálák száma korlátozott. A kör alakú tolózárak másik hátránya, hogy a kevésbé fontos skálák közelebb vannak a középponthoz, és kisebb pontosságúak. A legtöbb diák a lineáris csúszószabályokon tanulta meg a csúszószabályok használatát, és nem talált okot a váltásra.
Az egyik, világszerte napi használatban maradt számológép az E6B. Ez egy kör alakú számológép, amelyet először az 1930-as években készítettek a repülőgép-pilóták számára, hogy segítse a holtpont-számítást. A keretre nyomtatott skálák segítségével olyan különféle feladatokban is segít, mint az idő, a távolság, a sebesség és a hőmérséklet értékek átváltása, az iránytűhibák és az üzemanyag-felhasználás kiszámítása. Az úgynevezett "imakerék" ma is kapható a repülős boltokban, és továbbra is széles körben használják. Bár a GPS csökkentette a holtpontmérés használatát a légi navigációban, és a kézi számológépek átvették számos funkcióját, az E6B-t továbbra is széles körben használják elsődleges vagy tartalék eszközként, és a repülőiskolák többsége megköveteli, hogy tanulóik valamilyen szinten elsajátítsák.
1952-ben a svájci Breitling óragyártó cég bemutatta a Breitling Navitimer nevű pilóta karórát, amely beépített, repülési számításokra specializált kör alakú számológéppel rendelkezett. A Breitling által "navigációs számítógépként" emlegetett Navitimer körmércés számológép a repülési sebesség, az emelkedés/ereszkedés sebessége/ideje, a repülési idő, a távolság és az üzemanyag-fogyasztás, valamint a kilométer-navigációs mérföld és a gallon-liter üzemanyagmennyiség átváltási funkciókkal rendelkezett.
Anyagok
Hagyományosan kemény fából, például mahagóniból vagy bokszfából készültek, üvegből és fémből készült kurzorokkal. Legalább egy nagy pontosságú műszer acélból készült.
1895-ben egy japán cég, a Hemmi elkezdett bambuszból tolózárakat gyártani, amelyek előnye, hogy méretstabilak, erősek és természetesen önkenőek voltak. Ezeket a bambuszból készült tolózárakat 1933 szeptemberében vezették be Svédországban [2], és valószínűleg csak valamivel korábban Németországban. A skálák celluloidból vagy műanyagból készültek. A későbbi tolózárak műanyagból vagy műanyaggal festett alumíniumból készültek. A későbbi kurzorok akril vagy polikarbonátból készültek, tefloncsapágyakon csúszva.
Minden prémium kategóriás csúszószabályra számokat és skálákat véstek, majd festékkel vagy más gyantával töltötték ki. A festett vagy nyomtatott szabályozókat rosszabb minőségűnek tekintették, mivel a jelölések lekophatnak. Ennek ellenére a Pickett, Amerika valószínűleg legsikeresebb tolózárgyártó cége minden nyomtatott skálát elkészített. A prémium csúszószabályokhoz okos reteszek tartoztak, hogy a szabály véletlenül se essen szét, valamint ütközők, amelyek megvédték a skálákat és a kurzort az asztallapon való súrlódástól. A gravírozott jelölések ajánlott tisztítási módszere az acélgyapjúval való enyhe súrolás. A festett csúszószabályok és a gyengébb idegzetűek hígított kereskedelmi ablakmosó folyadékkal és puha ronggyal tisztíthatják.

Pickett kör alakú számológép két kurzorral. (4,25 in./10,9 cm átmérőjű) A hátoldalon további skála és egy kurzor található.

Egy egyszerű kör alakú, a Concise Co., Ltd. (Tokió, Japán) által gyártott, csak inverz, négyzetes és köbös skálával rendelkező, kör alakú számológép. A hátoldalon egy praktikus lista található 38 metrikus/birodalmi átváltási tényezővel.

Breitling Navitimer karóra kör alakú csúszásmérővel
Történelem
A számológépet 1620-1630 körül találták fel, nem sokkal azután, hogy John Napier közzétette a logaritmus fogalmát. Az oxfordi Edmund Gunter kifejlesztett egy olyan számolóeszközt, amely egyetlen logaritmusskálával rendelkezett, és további mérőeszközökkel szorzásra és osztásra is használható volt. E skála első leírását 1624-ben Párizsban Edmund Wingate (1593 körül - 1656) angol matematikus tette közzé "L'usage de la reigle de proportion en l'arithmetique & geometrie" című könyvében. A könyv egy kettős skálát tartalmaz, amelynek egyik oldalán egy logaritmikus skála, a másik oldalán pedig egy táblázatos skála található. 1630-ban a cambridge-i William Oughtred feltalált egy kör alakú csúszó szabályt, 1632-ben pedig két, kézzel összetartott Gunter-szabályt kombinált, és így olyan eszközt alkotott, amely felismerhetően a mai csúszó szabályt jelenti. Cambridge-i kortársához, Isaac Newtonhoz hasonlóan Oughtred is magánúton tanította elképzeléseit diákjainak, de késlekedett azok közzétételével, és Newtonhoz hasonlóan vitriolos vitába keveredett az elsőbbségről, egykori tanítványával, Richard Delamainnel és Wingate korábbi követeléseivel. Oughtred elképzeléseit csak tanítványa, William Forster 1632-ben és 1653-ban megjelent publikációi hozták nyilvánosságra.
1677-ben Henry Coggeshall megalkotta a két láb hosszúságú, faanyagok mérésére szolgáló, Coggeshall-szabásvonalat. Az ő tervezése és az eszköz felhasználása a matematikai vizsgálaton kívüli célt is adott a vonalzónak.
1722-ben Warner bevezette a két- és háromdekás skálákat, 1755-ben pedig Everard egy fordított skálát is tartalmazott; az összes ilyen skálát tartalmazó csúszószabályt általában "többfázisú" szabálynak nevezik.
1815-ben Peter Roget feltalálta a log log log csúszásmérőt, amely tartalmazott egy skálát, amely a logaritmus logaritmusát mutatta. Ez lehetővé tette a felhasználó számára, hogy közvetlenül elvégezze a gyökökkel és az exponensekkel kapcsolatos számításokat. Ez különösen hasznos volt a törtpotenciálok esetében.
Modern forma
A modernebb formát 1859-ben Amédée Mannheim francia tüzérhadnagy alkotta meg, "akinek szerencséje volt, hogy szabályát egy országos hírű cég készítette, és a francia tüzérség elfogadta". Nagyjából ebben az időben, amikor a mérnöki tevékenység elismert szakmai tevékenységgé vált, a csúszószabályok széles körben elterjedtek Európában. Az Egyesült Államokban csak 1881-ben váltak általánossá, amikor Edwin Thacher bevezetett egy hengeres szabályt. A duplex vonalzót William Cox találta fel 1891-ben, és a New York-i Keuffel and Esser Co. gyártotta.
A csillagászati munkához finom számításokra is szükség volt, és a 19. századi Németországban az egyik csillagvizsgálóban egy körülbelül 2 méter hosszú acél tolózárat használtak. Ehhez egy mikroszkóp volt csatlakoztatva, ami hat tizedesjegy pontosságot biztosított.
A második világháborúban a bombázók és a navigátorok, akiknek gyors számításokra volt szükségük, gyakran használtak speciális csúszószabályokat. Az amerikai haditengerészet egyik hivatala valóban tervezett egy általános, alumínium testtel és műanyag kurzorral ellátott "alvázat", amelybe speciális számításokhoz celluloid kártyákat lehetett helyezni (mindkét oldalra nyomtatott). Az eljárást repülőgépek hatótávolságának, üzemanyag-felhasználásának és magasságának kiszámítására találták ki, majd számos más célra is alkalmazták.
Az 1950-es és 1960-as években a számológép volt a mérnöki szakma szimbóluma (ugyanúgy, ahogy a sztetoszkóp az orvosi szakmát jelképezi).[] Wernher von Braun német rakétatudós két 1930-as évjáratú Nestler-féle csúszószabályozót hozott magával, amikor a második világháború után az Egyesült Államokba költözött, hogy az amerikai űrprogramon dolgozzon. Egész életében soha nem használt más zsebszámológépet; a csúszószabályok tökéletesen megfeleltek neki a rakéták tervezési paramétereinek és egyéb számadatok gyors becslésére. Az alumínium Pickett márkájú csúszódarabokat öt Apollo űrrepülésre vitték magukkal, többek között a Holdra is, a Pickett N600-as csúszódarabos dobozain elhelyezett reklámok szerint [3].
Egyes mérnökhallgatók és mérnökök tíz hüvelykes tolózárat hordtak övtáskában, és ez még az 1970-es évek közepén is gyakori látvány volt az egyetemeken. A diákok otthon vagy az irodában is tarthattak egy tíz- vagy húsz hüvelykes szabályt a precíziós munkához, miközben egy öt hüvelykes zsebmetsző szabályt hordtak magukkal.
2004-ben David B. Sher és Dean C. Nataro oktatáskutatók egy új típusú, a prosztaferezisre, a logaritmusok előtti, gyors termékszámítási algoritmusra épülő számolószabályt terveztek. A kezdeti prototípuson túl azonban kevés gyakorlati érdeklődés mutatkozott egy ilyen számológép megépítése iránt. [4]
Hanyatlás
A számológépek jelentősége kezdett csökkenni, ahogy az elektronikus számítógépek, amelyek az 1950-es években új, de nagyon ritka eszköznek számítottak, az 1960-as években széles körben elérhetővé váltak a műszaki dolgozók számára. A Fortran 1957-es bevezetése a számítógépeket praktikussá tette a szerényebb méretű matematikai problémák megoldására. Az IBM a tudományos és mérnöki piacra szánt, megfizethetőbb számítógépek sorozatát, az IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965) modelleket vezette be. John Kemeny BASIC programozási nyelve (1964) megkönnyítette a diákok számára a számítógépek használatát. A DEC PDP-8 miniszámítógépet 1965-ben mutatták be.
A számítógépek a számítás természetét is megváltoztatták. A csúszószabályokkal nagy hangsúlyt fektettek az algebra megmunkálására, hogy a kifejezéseket a lehető legjobban kiszámítható formába hozzák. A számológépek felhasználói egyszerűen csak közelítettek vagy elhagyhattak kisebb kifejezéseket, hogy egyszerűsítsék a számítást. A Fortran lehetővé tette, hogy a bonyolult képleteket a tankönyvekből az újrafogalmazás fáradtsága nélkül lehessen begépelni. A numerikus integrálás gyakran egyszerűbb volt, mint a nehéz problémák zárt formájú megoldásának keresése. A fiatal mérnök, aki számítógépes időt kért egy olyan probléma megoldására, amelyet néhány mozdulattal a számológépen is meg lehetett volna oldani, humoros közhely lett. Sok számítóközpontban egy bekeretezett számológépet függesztettek ki a falra a következő felirattal: "Vészhelyzet esetén törje be az üveget".
Egy másik lépés volt a csúszószabályok elektronikával való felváltása felé a tudományos és mérnöki használatra szánt elektronikus számológépek kifejlesztése. Az elsők közé tartozott az 1965-ben bemutatott Wang Laboratories LOCI-2, amely logaritmusokat használt a szorzáshoz és osztáshoz, valamint az 1968-ban bemutatott Hewlett-Packard HP-9100. A HP-9100 az exponenciálisok és logaritmusok mellett trigonometrikus funkciókkal is rendelkezett (sin, cos, tan). A CORDIC (koordinátaforgató digitális számítógép) algoritmust használta, amely lehetővé teszi a trigonometrikus függvények számítását csak eltolási és összeadási műveletekkel. Ez a módszer megkönnyítette az egyre kisebb tudományos számológépek kifejlesztését.
Az utolsó szöget a számológép koporsójába a zsebméretű tudományos számológépek megjelenése jelentette, amelyek közül az 1972-es Hewlett-Packard HP-35 volt az első. Az ilyen számológépek "számológépek" néven váltak ismertté, mivel a legtöbb vagy minden funkciót el tudtak látni egy számológépen. Több száz dolláros árával még ez is drágának számított a legtöbb diák számára. Míg a professzionális számológépek is elég drágák lehettek, a drogériákban gyakran 20 dollár alatti áron lehetett kapni az egyszerű műanyag modelleket. 1975-re azonban már 50 dollár alatt lehetett megvásárolni az alapvető négyfunkciós elektronikus számológépeket. 1976-ra a TI-30 már 25 dollár alatti tudományos számológépet kínált. Ezt követően a csúszószabályok piaca gyorsan kiszáradt, mivel a kis tudományos számológépek megfizethetővé váltak.

William Oughtred (1575-1660), a kör alakú számlap feltalálója.

Mérnök egy csúszó szabályt használ. A háttérben mechanikus számológép.

TI-30
Előnyök
- A tolózár hajlamos mérsékelni a "hamis pontosság" és a jelentőség tévedését. A tipikus pontosság, amely egy tolózár felhasználójának rendelkezésére áll, körülbelül három hely pontosságú. Ez jó összhangban van a mérnöki képletek bevitelére rendelkezésre álló adatok többségével. Egy modern zsebszámológép használatakor a pontosság hét vagy több tizedesjegyig is megjeleníthető, miközben a valóságban az eredmények soha nem lehetnek nagyobb pontosságúak, mint a rendelkezésre álló bemeneti adatok.
- A tolózár folyamatos becslést igényel az eredmények nagyságrendjéről. A csúszószámmérőn 1,5 × 30 (ami 45-nek felel meg) ugyanazt az eredményt mutatja, mint 1 500 000 × 0,03 (ami 45 000-nek felel meg). A mérnök feladata, hogy folyamatosan meghatározza az eredmények ésszerűségét, ami elveszhet, ha a számokat gondatlanul beírjuk egy számítógépes programba vagy számológépbe.
- Ha ugyanazzal a számmal történő szorzások vagy osztások sorozatát hajtjuk végre, a válasz gyakran manipuláció nélkül, pusztán egy pillantással meghatározható. Ez különösen hasznos lehet százalékok kiszámításakor, például tesztpontszámok esetében, vagy árak összehasonlításakor, például kilogrammonkénti dollárban kifejezve. Többféle sebesség-idő-távolság számítás végezhető el kéz nélkül, egy pillantással a tolómérővel.
- A tolózár nem függ az elektromosságtól.
- A tolózár egy könnyen reprodukálható technológia. Egy adott számológép-példányból egy hozzáértő kézműves többet is meg tud építeni kezdetleges anyagokból, nem ipari eljárásokkal.
- A csúszószabályok nagymértékben szabványosítottak, így nincs szükség arra, hogy bármit is újratanuljunk, ha más szabályra váltunk.
- A tolózárak sokoldalúak, és olyan helyzetekben és környezetekben is működtethetők, ahol az emberi felhasználó kézügyessége korlátozott lehet (például védőkesztyű használata miatt). Ezzel szemben egy számológépet nehéz lehet ilyen helyzetekben működtetni - egy számológépen való téves gomb megnyomásához hasonló hiba nem valószínű, hogy a számológépen való téves gomb megnyomásából adódó hibához hasonló hibát okozna.
- A csúszószabályok készülhetnek kartonból vagy papírból. Sok kartonból készült ingyenes táblázat vagy speciális számolóeszköz valójában speciális lineáris vagy kör alakú csúszószabály.
A számológép és az elektronikus számológép együttes használatának egyik előnye, hogy egy fontos számítást mindkettővel ellenőrizni lehet; mivel a két eszköz annyira különbözik egymástól, kicsi az esélye annak, hogy kétszer ugyanazt a hibát kövessük el.
Hátrányok
- A hibák mechanikai pontatlanságból adódhatnak.
- A számológörbével végzett számítások korlátozott pontosságúak az analóg bemenetek és kimenetek miatt. Ezzel szemben a diszkrét numerikus bemenet és a lebegőpontos elektronikus műveletek miatt még a szerényebb modern számológépek kimeneti felbontása is legalább hat szignifikáns számjegyű.
Kapcsolódó oldalak
Kérdések és válaszok
K: Mi az a tolózár?
V: A számológép egy mechanikus analóg számítógép, amelyet elsősorban szorzásra és osztásra, valamint olyan tudományos funkciókhoz használnak, mint a gyökszámítás, a logaritmusok és a trigonometria.
K: Melyek a különböző típusú csúszószabályok?
V: A tolószabályok lehetnek lineárisak vagy kör alakúak, és rendelkezhetnek a matematikai számításokhoz használt szabványosított jelölésekkel vagy skálákkal. Néhány speciális felhasználású csúszószabály a repülés vagy a pénzügyek számára készült, és az ilyen alkalmazásokhoz speciális skálákkal rendelkezik.
K: Ki találta fel a csúszó szabályt?
V: A számológépet William Oughtred találta fel John Napier logaritmusokkal kapcsolatos munkája alapján.
K: Mikor fejlesztették ki az elektronikus számológépeket?
V: Az elektronikus számológépeket az 1970-es évek előtt fejlesztették ki, de 1974 körül a zsebszámológép nagyrészt elavulttá tette a számológörbét.
K: Mit használtak leggyakrabban a természettudományok és a mérnöki tudományok területén az elektronikus számológépek kifejlesztése előtt?
V: Az elektronikus számológépek kifejlesztése előtt az emberek a tudományban és a mérnöki tudományokban leggyakrabban a számológépet használták.
K: Mennyi ideig használták az emberek a számológépet a digitális számítástechnikai eszközök megjelenése után is?
V: Az emberek az 1950-es és 1960-as években továbbra is használták a számológépet, még akkor is, amikor fokozatosan megjelentek a digitális számítástechnikai eszközök.
Keres