Pí (π) – Definíció és tulajdonságok: érték és irracionalitás
Ismerd meg a pí (π) definícióját, pontos értékét (3,14159...), irracionalitását és fő tulajdonságait — a kör, kerület és átmérő kapcsolatának érthető magyarázata.
A pí (vagy π) egy matematikai állandó. A kör körüli távolság és a kör átmérőjének hányadosa. Ez egy számot eredményez, és ez a szám mindig ugyanaz. A szám azonban meglehetősen furcsa. A szám 3,14159265358979323846... kezdődik, és végtelen tizedesjegy-sorozattal folytatódik. Az ilyen számokat irracionális számoknak nevezik.
Az átmérő a legnagyobb akkord, amely egy kör belsejébe illeszthető. A kör középpontján halad át. A kör körüli távolságot kerületnek nevezzük. Bár az átmérő és a kerület különböző körök esetében eltérő, a pi szám állandó marad: értéke soha nem változik. Ez azért van így, mert a kerület és az átmérő közötti kapcsolat mindig ugyanaz.
Számérték és egyszerű közelítések
A π pontos tizedesjegyei végtelen sorban követik egymást, és ismétlődés nélkül folynak. Gyakori egyszerű közelítések:
- 22/7 ≈ 3,142857 — egyszerű és széles körben használt közelítés (hibája ≈ 0,04%).
- 355/113 ≈ 3,14159292 — sokkal pontosabb rövid törtes közelítés (hibája ≈ 2,7×10−7).
- Gyakorlati számításokhoz gyakran elég 3,14 vagy 3,1416 használata attól függően, hogy mennyi pontosság szükséges.
Tulajdonságok
- Irracionalitás: π nem írható fel két egész szám hányadosaként (irracionális). Ennek egyik korai bizonyítását Johann Lambert adta 1761-ben.
- Transzcendencia: π nem csak irracionális, hanem transzcendens is — azaz nem gyök egyetlen nullátlan, egész együtthatós polinomnak. Ezt Ferdinand von Lindemann bizonyította 1882-ben. Ennek következménye többek között az, hogy a kör négyzetre hozatala (a négyzet átlójának megszerkesztése csak körzővel és vonalzóval úgy, hogy területe egy adott körével megegyezzen) lehetetlen.
- Kapcsolatok trigonometrikus és komplex függvényekkel: π megjelenik a trigonometrikus képletekben, a Fourier-analízisben és a komplex számok exponenciális kapcsolatában. Az egyik legismertebb formula: e^{iπ} + 1 = 0, azaz Euler azonossága, amely összekapcsolja az e, i, π, 1 és 0 állandókat.
- Radián mértékegység: A szög mérésekor π szerepel: 180° = π radián.
Formulák, ahol π szerepel
- Kör kerülete: C = π·d (d az átmérő).
- Más formában: C = 2·π·r (r a sugár).
- Kör területe: A = π·r².
Számítási módszerek és digitális rekordok
Az idők során sokféle módszert dolgoztak ki π értékének számítására: polygon-approximációk (Archimédész), sorfejtések (Leibniz-féle sor, gyorsabban konvergens sorok), iteratív algoritmusok (Gauss–Legendre), valamint modern gyors numerikus módszerek és nagy teljesítményű számítógépek. Az utóbbi évtizedekben rekordokat állítanak fel a számjegyek számában: többbillió tizedesjegy számítása is megtörtént.
Annak ellenére, hogy rengeteg jegyet kiszámoltak, az, hogy π „normális” szám-e (azaz a jegyek egyenletesen oszlanak-e meg minden számrendszerben), még bizonyítatlan kérdés a matematika számára.
Történeti és jelölési érdekességek
- A kör és a vele kapcsolatos állandók vizsgálata az ókorig nyúlik vissza (pl. Archimédész).
- A π betűt William Jones használta először 1706-ban a kör kerületének jelölésére, majd Leonhard Euler tette széles körben ismertté és elfogadottá a 18. században.
Alkalmazások
π megjelenik a mindennapi mérnöki számításokban (körök, hengerek, csővezetékek, fogaskerekek), a fizikában (hullámok, rezonanciák, kvantummechanika), a statisztikában és a számítástudományban (Fourier-transzformációk, jel- és képfeldolgozás). Emellett elméleti matematikai tételekben is kulcsfontosságú szerepet játszik.
Rövid összefoglalás
A π egy univerzális, állandó szám, amely a kör kerületének és átmérőjének arányát adja. Értéke körülbelül 3,1415926535..., irracionális és transzcendens. Számos matematikai képlet és fizikai törvény központi eleme, és a pontos értékét ma is folyamatosan számolják a nagyszabású számítástechnikai feladatokban.
π = C d {\displaystyle \pi ={\frac {C}{d}}} 
(pi egyenlő a kerület osztva az átmérővel).
A pí számok végtelen sora
Megközelítés
A pí formálisan gyakran π-nek vagy rövidítésként π görög betűnek írják. A pí irracionális szám, ami azt jelenti, hogy nem írható törtként ( a b {\displaystyle a \over b}
), ahol az "a" és a "b" egész számok (egész számok). Ez alapvetően azt jelenti, hogy a pi tizedesjegyektől jobbra eső számjegyei a végtelenségig tartanak anélkül, hogy egy mintában ismétlődnének, és hogy a pi pontos értékét nem lehet számként leírni. A pí értékét csak megközelíteni lehet, vagy olyan értékre mérni, amely a gyakorlati célokra elég közel van hozzá.
A pi-hez közeli érték 3.14159292653589793238462643... A pi egy gyakori tört közelítése 22 7 {\displaystyle 22 \over 7} 
, ami megközelítőleg 3,14285714 értéket ad. Ez a közelítés 0,04%-kal tér el a pi valódi értékétől. Bár ez a közelítés a való életben a legtöbbször elfogadott, a 355 113 {\displaystyle 355 \over 113}
törtérték pontosabb (körülbelül 3,14159292-t ad), és akkor használható, ha a pi-hez közelebbi értékre van szükség. A számítógépek segítségével jobban meg lehet közelíteni a pi értékét.
2019 márciusában Emma Haruka Iwao 31,4 billió számjegyre számította ki a pi értékét.
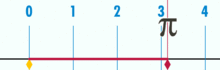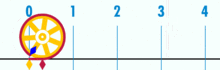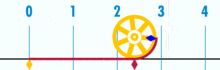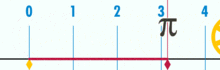
Egy ábra, amely megmutatja, hogyan lehet π-t megtalálni egy egy átmérőjű kör segítségével. Ennek a körnek a kerülete π.
Történelem
A pi értékét már az ókori indiai matematikusok, például Bhaskaracharya és Aryabhatta is ismerték.
A matematikusok évezredek óta ismerik a pí-t, mert ugyanennyi ideje dolgoznak körökkel. Az olyan régi civilizációk, mint a babilóniaiak, sok számjegyre tudták megközelíteni a pí értékét, például a 25/8 és a 256/81 törtét. A legtöbb történész úgy véli, hogy az ókori egyiptomiaknak nem volt fogalmuk a π-ről, és hogy a megfelelés véletlen egybeesés.
A pi-re vonatkozó első írásos említés i. e. 1900-ból származik. Kr. e. 1650 körül az egyiptomi Ahmes a Rhind-papiruszban adta meg az értéket. A babilóniaiak úgy tudták megállapítani, hogy a pi értéke valamivel nagyobb, mint 3, hogy egyszerűen készítettek egy nagy kört, majd egy darab kötelet ragasztottak a kerületére és az átmérőjére, feljegyezték a távolságukat, majd elosztották a kerületet az átmérővel.
A pi szám ismerete visszakerült Európába és a héberek kezébe, akik a számot a Biblia Ószövetségnek nevezett részében tették fontossá. Ezt követően a pi kiszámításának legelterjedtebb módja az volt, hogy egy sok oldalú alakzatot rajzoltak egy tetszőleges kör belsejébe, és az alakzat területét használták a pi kiszámításához. A görög filozófus Arkhimédész például egy 96 oldalú sokszög alakzatot használt a pi értékének megtalálására, de a kínaiak i. sz. 500-ban egy 16 384 oldalú sokszöget tudtak használni a pi értékének megtalálására. A görögök, mint például a klazomenai Anaxagorasz, a kör egyéb tulajdonságainak kiderítésével is foglalkoztak, például azzal, hogyan lehet a körökből négyzeteket készíteni, és hogyan lehet a pi számot négyzetre állítani. Azóta is sokan próbálnak egyre pontosabb értékeket találni a pi-nek.
| A pi története | ||
| Filozófus | Dátum | Megközelítés |
| i.sz. 150 körül | 3.1416 | |
| Zu Chongzhi | 430-501 CE | 3.1415929203 |
| al-Khwarizmi | i.sz. 800 körül | 3.1416 |
| al-Kashi | 1430 körül | 3.14159265358979 |
| Viète | 1540-1603 | 3.141592654 |
| Roomen | 1561-1615 | 3.14159265358979323 |
| Van Ceulen | 1600 körül | 3.14159265358979323846264338327950288 |
A 16. században egyre jobb és jobb módszerek váltak elérhetővé a pí meghatározására, például a francia jogász, François Viète által kifejlesztett bonyolult képlet. A görög "π" szimbólumot először William Jones 1706-ban írt esszéjében használták.
Egy Lambert nevű matematikus 1761-ben azt is kimutatta, hogy a pí szám irracionális, azaz a szokásos szabványok szerint nem írható fel törtként. Egy másik, Lindeman nevű matematikus 1882-ben azt is meg tudta mutatni, hogy a pí a transzcendenseknek nevezett számok csoportjába tartozik, amelyek olyan számok, amelyek nem lehetnek egy polinomegyenlet megoldása.
A pí a körökön kívül sok más dolog kiszámítására is használható. A pí tulajdonságai lehetővé tették, hogy a geometrián kívül, amely az alakzatokat tanulmányozza, a matematika számos más területén is felhasználható legyen. Néhány ilyen terület a komplex analízis, a trigonometria és a sorozatok.
Pi a való életben
Ma már különböző módszerek léteznek a π sok számjegyének kiszámítására. Ez azonban csak korlátozottan használható.
A pí néha bármely kör területének vagy kerületének kiszámítására használható. Egy kör kerületének kiszámításához a C (kerület) = π szorozva az átmérővel. Egy kör területének kiszámításához a π (sugár²) képletet használjuk. Ezt a képletet néha A = π r 2 {\displaystyle A=\pi r^{2}} 
, ahol r a kör sugarának változója, A pedig a kör területének változója.
Egy kör kerületének kiszámítása 1 mm-es hibával:
- 30 méteres körzethez 4 számjegyre van szükség.
- 10 számjegy a Föld sugarával megegyező sugaraknál
- 15 számjegy a Föld és a Nap közötti távolsággal megegyező sugarakhoz.
Az emberek általában azért ünneplik március 14-ét pí-napként, mert március 14-ét 3/14-nek is írják, ami a pí közelítésében az első három számot, a 3,14-et jelenti. A pí napja 2001 folyamán kezdődött.
Kapcsolódó oldalak
Kérdések és válaszok
K: Mi az a ً szám?
V: A ً egy matematikai állandó, amely a kör kerületének és átmérőjének aránya.
K: Mit eredményez ez a szám?
V: Ez egy számot eredményez, és ez a szám mindig ugyanaz.
K: Hogyan kezdődik ez a szám?
V: A szám úgy kezdődik, hogy 3,14159292653589793... és vég nélkül folytatódik.
K: Milyen típusú számok ezek?
V: Ezeket a számokat irracionális számoknak nevezzük.
K: Mekkora a kör átmérője?
V: A kör átmérője az a legnagyobb akkord, amely a középpontján áthaladva elfér benne.
K: Mi a kör kerülete? V: A kör körüli távolságot a kör kerületének nevezzük.
K: A pi a különböző köröktől függetlenül állandó marad? V: Igen, a pi a különböző köröktől függetlenül állandó marad, mert a kerületük és az átmérőjük közötti kapcsolat mindig ugyanaz marad.
Keres