Felületi integrál
A matematikában a felületi integrál egy felület (amely lehet egy görbe is a térben) felett vett határozott integrál. Ahogyan a vonalintegrál egy dimenziót vagy egy változót kezel, a felületi integrál két dimenzió mentén kettős integrálnak tekinthető. Egy felületet tekintve integrálhatunk annak skalármezői (azaz olyan függvények, amelyek számokat adnak vissza értékként) és vektormezői (azaz olyan függvények, amelyek vektorokat adnak vissza értékként) felett.
A felületi integrálok a fizikában, különösen az elektromágnesesség klasszikus elméletében találnak alkalmazást.
A felületi integrál meghatározása a felület kis felületi elemekre való felosztásán alapul.
Egyetlen felületelem illusztrációja. Ezeket az elemeket végtelenül kicsinyre alakítják a korlátozási eljárással, hogy a felületet megközelítsék.
Skalármezők felületi integráljai
Tekintsünk egy S felületet, amelyen egy f skalármezőt definiálunk. Ha úgy gondoljuk, hogy S valamilyen anyagból van, és minden x-re az S-ben az f(x) szám az anyag sűrűsége x-nél, akkor az f S feletti felületi integrálja az S egységnyi vastagságra jutó tömege. (Ez csak akkor igaz, ha a felület egy végtelenül vékony héj.) A felületi integrál kiszámításának egyik megközelítése az, hogy a felületet sok nagyon kis darabra osztjuk, feltételezzük, hogy minden egyes darabon a sűrűség megközelítőleg állandó, megtaláljuk az egyes darabok egységnyi vastagságra eső tömegét úgy, hogy megszorozzuk a darab sűrűségét a területével, majd az így kapott számokat összegezzük, hogy megtaláljuk S egységnyi vastagságra eső teljes tömegét.
Ahhoz, hogy explicit képletet találjanak a felületi integrálra, a matematikusok S-t úgy paraméterezik, hogy S-re egy görbületi koordinátarendszert tekintenek, mint a szélességi és hosszúsági fokokat egy gömbön. Legyen egy ilyen paraméterezés x(s, t), ahol (s, t) a sík valamely T tartományában változik. Ekkor a felszíni integrál a következővel adódik
∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {\displaystyle \int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt} 
ahol a jobb oldali oszlopok közötti kifejezés az x(s, t) parciális deriváltjai kereszttételének nagysága.
Például egy általános funkcionális alakzat, mondjuk z = f ( x , y ) {\displaystyle z=f\,(x,y)}
felületének meghatározásához a következővel kell számolnunk
A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\displaystyle A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy} 
ahol r = ( x , y , z ) = ( x , y , f ( x , y ) ) {\displaystyle \mathbf {r} =(x,y,z)=(x,y,f(x,y))}
. Tehát ∂ r ∂ x = ( 1 , 0 , f x ( x , y ) ) {\displaystyle {\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))} 
, és ∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ) {\displaystyle {\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))}
. Tehát,
A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle {\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}}\,\,dx\,dy\end{aligned}}}}} 
amely egy általános funkcionális alakzat felületének meghatározására használt képlet. A fenti második sorban szereplő vektort a felületre vonatkozó normálvektorként ismerhetjük fel.
Megjegyzendő, hogy a kereszttétel jelenléte miatt a fenti képletek csak háromdimenziós térbe ágyazott felületek esetén működnek.
Vektormezők felületi integráljai
Tekintsünk egy v v vektormezőt S-en, azaz minden x-hez S-ben v(x) egy vektor.
A felületi integrál a skalármező felületi integráljának definíciója szerint komponensenként definiálható; az eredmény egy vektor. Ez vonatkozik például egy elektromosan töltött felület által okozott elektromos mezőre egy fix ponton, vagy egy anyaglap által okozott gravitációra egy fix ponton. Egy felületen áthaladó mágneses fluxus is kiszámítható.
Alternatív megoldásként a matematikusok integrálhatják a vektormező normális komponensét; az eredmény egy skalár. Egy példa egy S-en átáramló folyadék, így v(x) határozza meg a folyadék sebességét x-nél. A fluxus az S-en átáramló folyadék mennyisége egységnyi idő alatt.
Ez az ábra azt jelenti, hogy ha a vektormező minden egyes ponton érintőleges az S-re, akkor a fluxus nulla, mert a folyadék csak az S-sel párhuzamosan áramlik, és sem befelé, sem kifelé. Ez azt is jelenti, hogy ha v nem csak S mentén áramlik, azaz ha v-nek van egy érintőleges és egy normális komponense is, akkor csak a normális komponens járul hozzá a fluxushoz. Ezen okfejtés alapján a fluxus megtalálásához minden egyes pontban ki kell vennünk a v és az S-re merőleges egységfelület pontszorzatát, ami egy skalármezőt ad, és a kapott mezőt a fentiek szerint integrálnunk kell. Ez a következő képletet adja
∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . {\displaystyle \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt. } 
A kifejezés jobb oldalán található kereszttag a paraméterezés által meghatározott felületi normál.
Ez a képlet határozza meg a bal oldali integrált (figyeljük meg a pontot és a vektoros jelölést a felszíni elemre).
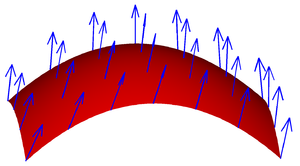
Egy vektormező egy felületen.
Felületi integrálokra vonatkozó tételek
A differenciálgeometria és a vektorszámítás segítségével számos hasznos eredményt lehet levezetni a felületi integrálokra, például a divergencia-tételt és annak általánosítását, a Stokes-tételt.
Speciális problémák
Paraméterezés megváltoztatása
A fenti értekezés a felületintegrált a felület S paraméterezésével határozta meg. Egy adott felületnek több paraméterezése is lehet. Ha például az Északi és a Déli-sark helyét áthelyezzük egy gömbön, a szélességi és hosszúsági fokok a gömb összes pontján megváltoznak. Természetes kérdés, hogy a felületintegrál definíciója függ-e a választott paraméterezéstől. A skalármezők integráljai esetében a válasz erre a kérdésre egyszerű, a felületi integrál értéke ugyanaz lesz, függetlenül attól, hogy milyen parametrizációt használunk.
A vektormezők integráljai bonyolultabbak, mivel a felületi normális is szerepel. A matematikusok bebizonyították, hogy ugyanazon felület két olyan parametrizációja esetén, amelyek felületi normálisai ugyanabba az irányba mutatnak, mindkét parametrizáció ugyanazt az értéket adja a felületi integrálra. Ha azonban e paraméterezések normálisai ellentétes irányba mutatnak, akkor az egyik paraméterezéssel kapott felületi integrál értéke a másik paraméterezéssel kapott érték negatívja. Ebből következik, hogy adott felület esetén nem kell ragaszkodnunk egyetlen paraméterezéshez sem; de vektormezők integrálásakor előre el kell döntenünk, hogy a normálisok melyik irányba mutatnak, és ezután bármelyik paraméterezést kell választanunk, amelyik megfelel ennek az iránynak.
A paraméterezések a felület egyes részein működnek
Egy másik probléma az, hogy néha a felületek paraméterei nem fedik le az egész felületet; ez igaz például egy (véges magasságú) henger felületére. A kézenfekvő megoldás ilyenkor az, hogy a felületet több darabra osztjuk, minden egyes darabra kiszámítjuk a felületintegrált, majd mindet összeadjuk. Valóban így működik a dolog, de vektormezők integrálásakor ismét ügyelni kell arra, hogy a felület egyes darabjaira hogyan választjuk meg a normális-pontvektort, hogy amikor a darabokat összerakjuk, az eredmények konzisztensek legyenek. A henger esetében ez azt jelenti, hogy ha úgy döntünk, hogy az oldalsó területre a normálirány a testből kifelé mutat, akkor a felső és alsó kör alakú részekre is a normáliránynak a testből kifelé kell mutatnia.
Nem konzisztens felületi normálisok
Végül, vannak olyan felületek, amelyeknek nem minden pontján van felületi normálisuk, és amelyeknél az eredmények konzisztensek (például a Möbius-szalag). Ha egy ilyen felületet darabokra bontunk, minden egyes darabon kiválasztunk egy paraméterezést és a megfelelő felületi normált, majd a darabokat összerakjuk, a különböző darabokból származó normális vektorok nem egyeztethetők össze. Ez azt jelenti, hogy a két darab közötti bizonyos csomópontban a normálvektorok ellentétes irányba fognak mutatni. Az ilyen felületet nem orientálhatónak nevezzük. A vektormezők nem integrálhatók a nem orientálható felületekre.
Kapcsolódó oldalak
- Divergencia-tétel
- Stokes-tétel
- Vonali integrál
- Térfogati integrál
- Kartéziánus koordinátarendszer
- Térfogat- és felületelemek gömbi koordinátarendszerben
- Térfogat- és felületelemek hengeres koordinátarendszerben
- Holstein-Herring módszer
