Pont szorzat

Meghatározás

Két vektor a = [a₁ , a₂ , ..., a_n ] és b = [b₁ , b₂ , ..., b_n ] ponttermelése a következő:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}}

ahol Σ az összegző jelölés ( az összes kifejezés összege), n pedig a vektortér dimenziója.

A 2 dimenzióban az [a,b] és [c,d] vektorok pontgyakorisága ac + bd. Ugyanígy a 3 dimenzióban az [a,b,c] és a [d,e,f] vektorok pontgyöke ad + be + cf. Például két háromdimenziós vektor [1, 3, -5] és [4, -2, -1] pontgyöke a következő.

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.}

Geometriai értelmezés

Az euklideszi geometriában a pontszorzat, a hossz és a szög összefügg egymással. Egy a vektor esetén az a - a pontszorzat az a hosszának négyzete, vagy

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}}

ahol ||a|| az a hosszát (nagyságát) jelöli. Általánosabban, ha b egy másik vektor.

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,}

ahol ||a|| és ||b|| jelöli a és b hosszát, θ pedig a köztük lévő szöget.

Ez a képlet átrendezhető, hogy meghatározzuk a két nem nulla vektor közötti szög nagyságát:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {\mathbf {a}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)}

A vektorokat először egységvektorokká is alakíthatjuk, ha elosztjuk őket a nagyságukkal:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}}}

akkor a θ szöget a következő adja meg

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}\cdot {\boldsymbol {\hat {b}})}}

Mivel a 90° koszinusza nulla, két egymásra merőleges (merőleges) vektor pontszorzata mindig nulla. Továbbá két vektor akkor és csak akkor tekinthető ortogonálisnak, ha a pontproduktumuk nulla, és mindkettőnek nem nulla a hossza. Ez a tulajdonság egy egyszerű módszert biztosít az ortogonalitás feltételének vizsgálatára.

Néha ezeket a tulajdonságokat a pontszorzat meghatározására is használják, különösen 2 és 3 dimenzióban; ez a definíció egyenértékű a fenti definícióval. Magasabb dimenziók esetén a képlet használható a szög fogalmának meghatározására.

A geometriai tulajdonságok azon alapulnak, hogy az alap ortonormális, azaz páronként egymásra merőleges, egységnyi hosszúságú vektorokból áll.

Skálar vetület

Ha mind a, mind b hossza egy (azaz egységvektorok), akkor a pontproduktumuk egyszerűen a köztük lévő szög koszinuszát adja.

Ha csak b egy egységvektor, akkor az a - b pontszorzat adja |a| cos(θ), azaz a b irányába vetített a vetület nagyságát, mínusz előjellel, ha az irány ellentétes. Ezt nevezzük az a skaláris vetületének b-re, vagy az a skaláris komponensének b irányában (lásd az ábrát). A pontszorzat e tulajdonságának számos hasznos alkalmazása van (lásd például a következő szakaszt).

Ha sem a, sem b nem egységvektor, akkor például a b irányába vetített a vetület nagysága a - (b / |b|), mivel a b irányába vetített egységvektor b / |b|.

Forgatás

Annak az ortonormális alapnak a forgatását, amely alapján az a vektort ábrázoljuk, egy R forgatási mátrixszal való szorzással kapjuk meg. Ez a mátrixszorzás nem más, mint a pontproduktumok sorozatának kompakt megjelenítése.

Legyen például

• B₁ = {x, y, z} és B₂ = {u, v, w} legyen ugyanazon R³ tér két különböző ortonormális bázisa, B₂ pedig B₁ egyszerű elforgatásával kapható,
• a₁ = (a_x , a_y , a_z ) az a vektort B₁ szempontjából képviseli,
• a₂ = (a_u , a_v , a_w ) ugyanazt a vektort képviseli a B₂ elforgatott bázis szempontjából,
• u₁ , v₁ , w₁ legyenek az u, v, w elforgatott bázisvektorok B₁ formájában ábrázolva.

Ezután a forgatás B ₁-ról B ₂-re a következőképpen történik:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}}_{1}\\{\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}. }

Vegyük észre, hogy az R forgatási mátrixot az u₁ , v₁ , w₁ elforgatott bázisvektorok felhasználásával állítjuk össze, és ezek a vektorok egységvektorok. Definíció szerint Ra₁ az R három sora és az a₁ vektor közötti ponttétel sorozatából áll. E ponttételek mindegyike meghatározza az a skalárkomponensét egy elforgatott bázisvektor irányában (lásd az előző szakaszt).

Ha a₁ nem oszlopvektor, hanem sorvektor, akkor R-nek az oszlopaiban kell tartalmaznia a forgatott bázisvektorokat, és utólagosan kell szoroznia a₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}}_{2}={\mathbf {a}}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}}_{1}&{\mathbf {v}}}_{1}\cdot {\mathbf {a}}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. }

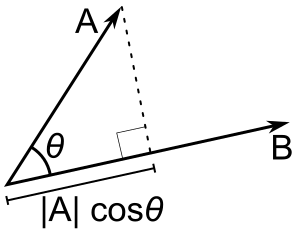
A - B = |A| |B| cos(θ). |A| cos(θ) az A skaláris vetülete B-re.

Fizika

A fizikában a nagyság fizikai értelemben skalár, azaz a koordinátarendszertől független fizikai mennyiség, amelyet egy számérték és egy fizikai egység szorzataként fejeznek ki, nem csak egy számmal. A pontszorzat szintén skalár ebben az értelemben, a képlet által megadott, a koordinátarendszertől független érték. Példa:

• A mechanikai munka az erő- és elmozdulásvektorok ponttermelése.
• A mágneses fluxus a mágneses mező és a területvektorok szorzata.
• A térfogatáram a folyadék sebességének és a területvektoroknak a szorzata.

Tulajdonságok

A következő tulajdonságok érvényesek, ha a, b és c valós vektorok, r pedig skalár.

A pontszorzat kommutatív:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . }

A pontszorzat a vektorok összeadásánál elosztó:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . }

A pontszorzat bilineáris:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). }

Ha egy skalárértékkel szorozzuk, a pontszorzat megfelel:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )} }

(ez utóbbi két tulajdonság az első kettőből következik).

Két nem nulla a és b vektor akkor és csak akkor merőleges egymásra, ha a - b = 0.

A közönséges számok szorzásától eltérően, ahol ha ab = ac, akkor b mindig egyenlő c-vel, kivéve, ha a nulla, a pontszorzat nem engedelmeskedik a törlési törvénynek:

Ha a - b = a - c és a ≠ 0, akkor a disztributív törvény alapján leírhatjuk: a - (b - c) = 0; a fenti eredmény szerint ez csak azt jelenti, hogy a merőleges (b - c)-re, ami még mindig lehetővé teszi, hogy (b - c) ≠ 0, tehát b ≠ c.

Feltéve, hogy az alap ortonormális, a pontszorzat invariáns az alap izometrikus változtatásai esetén: forgatások, tükrözések és kombinációk, az origó fixen tartása mellett. A fent említett geometriai értelmezés erre a tulajdonságra támaszkodik. Más szóval egy tetszőleges számú dimenziójú ortonormális tér esetén a pontszorzat invariáns egy ortogonális mátrixon alapuló koordinátatranszformáció esetén. Ez a következő két feltételnek felel meg:

• Az új bázis ismét ortonormális (azaz a régiben kifejezve ortonormális).
• Az új bázisvektorok hossza megegyezik a régiekével (azaz a régi bázist tekintve egységnyi hosszúságúak).

Ha a és b függvények, akkor a - b deriváltja a' - b + a - b'.

Háromszoros termékbővítés

Ez egy nagyon hasznos azonosság (Lagrange-formula néven is ismert), amely a pont- és kereszttételeket foglalja magában. Ez a következőképpen írható le

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )- -\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )} }

ami könnyebben megjegyezhető "BAC mínusz CAB", szem előtt tartva, hogy mely vektorok vannak pontozva. Ezt a képletet a fizikában gyakran használják a vektorszámítások egyszerűsítésére.

A geometriai értelmezés bizonyítása

Tekintsük az Rⁿ elemét.

v = v 1 e ^ 1 + v 2 e ^ 2 + .. . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

A Pitagorasz-tétel ismételt alkalmazásával a hosszára |v| a következő eredményt kapjuk

| v | 2 = v 1 2 + v 2 2 + . . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

De ez ugyanaz, mint

v ⋅ v = v 1 2 + v 2 2 + . . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

tehát arra következtetünk, hogy a v v vektor és önmaga ponttermelése adja a vektor négyzetes hosszát.

Lemma 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Tekintsünk most két, az origótól kiinduló a és b vektort, amelyeket θ szög választ el egymástól. Egy harmadik c vektor a következőképpen definiálható

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}}\ \mathbf {a} -\mathbf {b} .\,}

létrehozva egy háromszöget a, b és c oldalakkal. A koszinuszok törvénye alapján a következő állítással rendelkezünk

| c | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Ha az 1. lemma szerint a négyzetes hosszúságokat ponttételekkel helyettesítjük, akkor megkapjuk a következőt

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\\mathbf {b} |\cos \theta .\,} (1)

De mivel c ≡ a - b, ezért azt is megkapjuk, hogy

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} ,

amely a disztributív törvény szerint a következőre bővül

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} (2)

A két c - c egyenlet (1) és (2) összevonásával megkapjuk a következőt

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\\mathbf {b} |\cos \theta .\,}

Ha mindkét oldalból kivonjuk a - a + b - b-t, és elosztjuk -2-vel, akkor a - a + b - b marad.

a ⋅ b = | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\\mathbf {b} |\cos \theta .\,}

Q.E.D.

Generalizáció

A belső szorzat általánosítja a pontszorzatot absztrakt vektorterekre, és általában a következővel jelöljük: ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } . A pontszorzat geometriai értelmezésének köszönhetően az a vektor ||a|| normája egy ilyen belső szorzat térben a következőképpen definiálható

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

úgy, hogy általánosítja a hosszúságot, és a két a és b vektor közötti θ szöget a következővel

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \\\mathbf {a} \|\,\|\|\mathbf {b} \|}}. }

Két vektor akkor tekinthető ortogonálisnak, ha belső szorzatuk nulla.

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \szög =0.}

Komplex bejegyzésekkel rendelkező vektorok esetén a pontszorzat adott definíciójának használata egészen más geometriai tulajdonságokhoz vezetne. Például egy vektor és önmaga ponttermelése tetszőleges komplex szám lehet, és lehet nulla anélkül, hogy a vektor zérusvektor lenne; ez viszont súlyos következményekkel járna az olyan fogalmakra, mint a hosszúság és a szög. Számos geometriai tulajdonság megmenthető, a skaláris szorzat szimmetrikus és bilineáris tulajdonságainak feladása árán, ha alternatív módon definiáljuk a következőket

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

ahol b_i a b _ikomplex konjugáltja. Ekkor bármely vektor skaláris szorzata önmagával nemnegatív valós szám, és a nullvektor kivételével nem nulla. Ez a skaláris szorzat azonban nem lineáris b-vel (hanem inkább konjugált lineáris), és a skaláris szorzat sem szimmetrikus, mivel

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}} .

A skaláris szorzatnak ez a típusa mindazonáltal igen hasznos, és elvezet a hermitiánus forma és az általános belső szorzatú terek fogalmához.

A Frobenius-féle belső szorzat általánosítja a pontszorzatot a mátrixokra. Két azonos méretű mátrix megfelelő összetevői szorzatának összegeként definiáljuk.

Általánosítás tenzorokra

Egy n rendű tenzor és egy m rendű tenzor közötti pontszorzat egy n+m-2 rendű tenzor. A pontszorzatot mindkét tenzor egyetlen indexének szorzásával és összegzésével kapjuk meg. Ha A {\displaystyle \mathbf {A} } és B {\displaystyle \mathbf {B} } két tenzor, amelyeknek A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }}} és B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}}} elemei a pontszorzat A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } a következők szerint adódnak

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}}}

Ez a definíció természetesen visszavezethető a vektorokra alkalmazott standard vektorpontszorzatra, illetve mátrixokra alkalmazott mátrixszorzatra.

Alkalmanként a kettős pontproduktumot használják a két index közötti szorzás és összegzés ábrázolására. Két másodrendű tenzor kettős pontszorzata skalár.

Kapcsolódó oldalak

• Cauchy-Schwarz egyenlőtlenség
• Kereszt termék
• Mátrix szorzás
• Fizika