Henger: definíció, felszín és térfogat, típusok és geometriai tulajdonságok

Átfogó útmutató a hengerhez: definíció, felszín- és térfogatszámítás, típusok (kör-, elliptikus, parabolikus) és fontos geometriai tulajdonságok példákkal.

Szerző: Leandro Alegsa

05-02-2026 21:28

A henger az egyik legalapvetőbb görbe geometriai alakzat, amelynek felületét egy adott vonalszakasztól, a henger tengelyétől meghatározott távolságban lévő pontok alkotják. Az alakzatot úgy is felfoghatjuk, mint egy kör alakú prizmát. Mind a felületet, mind a benne létrejövő szilárd alakzatot hengerrel nevezhetjük. A henger felületét és térfogatát már az ókor óta tanulmányozzák, és a mai napig fontos szerepet játszik a matematikában, a fizikában és a műszaki gyakorlatban.

Mit értünk henger alatt?

Általánosan a henger olyan felület vagy test, amelyet egyenesek (a generátorok vagy oldalgörbék) egyparaméteres családja hoz létre egy adott görbe mentén történő eltolással. A leggyakrabban tárgyalt alakzat a körhenger (kör alakú alapokkal), amelynél az alapok párhuzamos körlapok, és a két alap közötti távolság a magasság (h). A henger részei magyarul: alap(ok), palást (oldalfelület), tengely és generátrix (a palástot alkotó egyenes).

Típusok

Körhenger (kör alakú henger): mindkét alap kör, ez a leggyakoribb példa. Ha a generatrix merőleges az alapokra, akkor merőleges vagy jobb henger (jobb körhenger).
Ferde henger: a generatrixok nem merőlegesek az alapokra; a palást ferdén áll. Fontos tulajdonság: azonos alap- és magasságadatok mellett a ferde henger térfogata megegyezik a megfelelő merőleges hengerével (Cavalieri-elv).
Elliptikus, parabolikus és hiperbolikus hengerek: differenciálgeometriai értelemben a henger olyan szabályos felület, amelyet párhuzamos egyenesek egyparaméteres családja fed le. Az olyan hengert, amelynek keresztmetszete ellipszis, parabola vagy hiperbola, elliptikus henger, parabolikus henger vagy hiperbolikus henger nevezik. Ezeknél az alap görbéje nem kör, ezért a képletek és tulajdonságok általánosabbak vagy eltérők lehetnek.
Poligonális alapú hengerek: a prizma speciális esetei, ha az alap többélű (pl. háromszög, négyszög), ezeket gyakran prizmának nevezik, de formálisan a „henger” fogalma kiterjeszthető ezekre is.

Felszín és térfogat – alapképletek (körhenger esetén)

A körhenger fontos paraméterei: sugár (r), magasság (h) és a henger tengelye. A legegyszerűbb és leggyakrabban használt képletek:

Alap területe: A_alap = π r²
Oldalfelület (palást) területe: A_palást = (alap kerülete) × h = 2π r h
Teljes felszín: A_teljes = 2 · A_alap + A_palást = 2π r² + 2π r h = 2π r (r + h)
Térfogat: V = A_alap · h = π r² h

Fontos megjegyezni: a palást nettója egy téglalap, amelynek méretei 2πr × h; ehhez járulnak a két alapkör.

Általános hengerek – képletek és megjegyzések

Ha az alap egy tetszőleges sík görbe területe S, akkor a henger térfogata általánosan V = S · h (függetlenül attól, hogy a henger ferde-e), azaz a térfogat a alap területének és a magasságnak a szorzata.
Elliptikus alap esetén az alap területe A = π a b (ahol a és b az ellipszis féltengelyei). A palást területe a görbe kerületének és a magasságnak a szorzata — az ellipszis kerülete viszont nincs zárt alakban, ezért közelítést szoktak használni (például Ramanujan-féle közelítés).
Parabolikus vagy hiperbolikus hengerek esetén a „palást” görbe mentén halad, és a felület geometriája különbözik a körhengerétől; ilyen felületek fontosak differenciálgeometriában és PDE-kben.

Geometriai és analitikus jellemzés

Analitikusan egy jobb körhengert, amelynek tengelye a z-tengely, leírhatunk az egyenlettel x² + y² = r², ahol z korlátolt (például 0 ≤ z ≤ h). A palást paraméterezhető: (r cos t, r sin t, z) (t ∈ [0, 2π), z ∈ [0, h]).

Fontos tulajdonságok és tétel

Szimmetria: a jobb körhenger forgásszimmetrikus tengelye körül és tükrözhető a középperpenikuláris síkra.
Cavalieri-elv: azonos alap- és magasságadatok mellett különböző ferdék ugyanazt a térfogatot adják (az integrálás vagy a lemezes módszer alapján).
Hálók (net): a henger hálója egy téglalap (palást) és két kör (alapok). A téglalap szélessége a kör kerülete (2πr), magassága a h.

Példák, mértékegységek és alkalmazások

Példa: ha r = 2 cm és h = 5 cm, akkor V = π · 2² · 5 = 20π cm³, A_palást = 2π · 2 · 5 = 20π cm², A_teljes = 2π · 2 (2 + 5) = 28π cm².

Alkalmazások: hengereket találunk csövekben, tárolótartályokban, hengerekben (gépészet), hengeres csövek hidraulikában, mérőeszközökben, továbbá a matematika és a fizika számos területén (pl. térfogatszámítás, hővezetés csőformákban, áramlástan).

Rövid történeti és didaktikai megjegyzés

A hengerrel kapcsolatos alapfogalmak és képletek antik forrásokból erednek, majd az analízis kialakulásával egyszerű integrálással könnyen meghatározhatók. A henger jó példája a testek síkbeli metszetekből való összerakásának, és didaktikailag is gyakran használják a térfogatszámítás bemutatására.

Összefoglalva: a henger egyszerű, mégis sokoldalú geometriai alakzat — a körhengerre vonatkozó zárt képletek könnyen alkalmazhatók a gyakorlatban, míg az általános hengerek (elliptikus, parabolikus, hiperbolikus) bővítik a vizsgálat tárgyát a differenciálgeometriában és a műszaki alkalmazásokban.

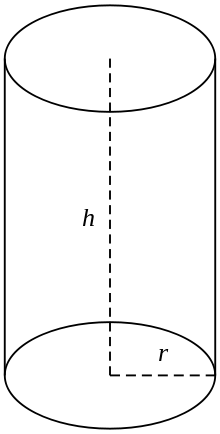
Egy derékszögű kör alakú henger

Általános használat

A közhasználatban a henger alatt a derékszögű körhenger véges metszetét értjük, azaz azt a hengert, amelynek generáló vonalai merőlegesek az alapokra, és amelynek végei két kör alakú felületet alkotnak, mint a (jobb oldali) ábrán. Ha a henger sugara $r$ és hossza (magassága) h, akkor térfogata a következő:

$V$ $= πrh 2$

és a felülete:

a felső rész területe $(πr 2) +$
az alsó rész területe $(πr 2) +$
az oldal területe ( $2πrh$ ).

Ezért a felső vagy alsó rész (oldalirányú terület) nélkül a felület:

$A$ $= 2πrh$ .

A felső és az alsó részen a felület:

$A$ $= 2πr 2 + 2πrh = 2πr(r + h)$ .

Adott térfogat esetén a legkisebb felületű henger $h = 2r$ . Adott felület esetén a legnagyobb térfogatú henger $h = 2r, azaz$ a henger befér egy kockába (magasság = átmérő).

Volume

Egy $h$ egységnyi magasságú, derékszögű körhenger és egy $r$ egységnyi sugarú alap, amelynek koordinátatengelyei úgy vannak megválasztva, hogy az origó az egyik alap középpontjában van, a magasságot pedig a pozitív x-tengely mentén mérjük. Az origótól $x$ egységnyi távolságra lévő síkmetszet területe $A (x)$ négyzetegység, ahol

A ( x ) = π r {\displaystyle2 A(x)=\pi r^{2}} $A(x)=\pi r^{2}$

vagy

A ( y ) = π r {\displaystyle2 A(y)=\pi r^{2}} $A(y)=\pi r^{2}$

Egy térfogatelem egy $Aw i$ négyzetméter alapterületű és $Δx i$ egység vastagságú derékszögű henger. Így ha V köbméter egység a jobb oldali körhenger térfogata, a Riemann-összegek szerint,

V o l u m e o f c y l i n d e r = lim | | | Δ → |0 | ∑ i = n 1A ( w i ) Δ i x {\displaystyle \mathrm {Volume\;of\;cylinder} =\lim _{|\\Delta \to 0|||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x} $\mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x$

= ∫ h 0A ( y ) d2 y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy} $=\int _{0}^{h}A(y)^{2}\,dy$

= ∫ h0 π r d2 y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy} $=\int _{0}^{h}\pi r^{2}\,dy$

= π r h 2{\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

Hengeres koordináták használatával a térfogat kiszámítható integrálással a következő területre

= ∫ h0 ∫ π02 ∫ r0 s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,ds\,d\phi \,dz} $=\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz$

= π r h 2{\displaystyle =\pi \,r^{2}\,h\,} $=\pi \,r^{2}\,h\,$

Hengeres szelvény

A hengeres metszetek a hengerek és a síkok metszéspontjai. Egy derékszögű körhenger esetében négy lehetőség van. A hengert érintő sík egyetlen egyenes vonalban találkozik a hengerrel. Önmagával párhuzamosan mozgatva a sík vagy nem metszi a hengert, vagy két párhuzamos egyenesben metszi azt. Minden más sík ellipszisben, vagy ha merőleges a henger tengelyére, akkor körben metszi a hengert.

Más típusú hengerek

Az elliptikus henger, vagy cylindroid egy kvadrikus felület, amelynek a következő egyenlete van kartéziánus koordinátákban:

( x a ) +2 ( y b ) =21 . {\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}}\right)^{2}=1.} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.$

Ez az egyenlet egy elliptikus hengerre vonatkozik, amely a közönséges körhenger ( $a = b$ ) általánosítása. Még általánosabb az általánosított henger: a keresztmetszet bármilyen görbe lehet.

A henger egy degenerált kvadrikus, mivel legalább az egyik koordináta (ebben az esetben $z$ ) nem szerepel az egyenletben.

A ferde henger felső és alsó felülete eltolódik egymástól.

Vannak más, szokatlanabb típusú hengerek is. Ezek a képzeletbeli elliptikus hengerek:

( x a ) +2 ( y b ) = 2- 1{\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}}\right)^{2}=-1}} $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1$

a hiperbolikus henger:

( x a ) 2- ( y b ) = 2{\displaystyle1 \left({\frac {x}{a}}}\right)^{2}-\left({\frac {y}{b}}}\right)^{2}=1} $\left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1$

és a parabolikus henger:

x +2 a2 y =0 . {\displaystyle x^{2}+2ay=0.\,} $x^{2}+2ay=0.\,$

Egy elliptikus henger

A projekciós geometriában a henger egyszerűen egy kúp, amelynek csúcsa a végtelenben van, ami vizuálisan megfelel annak, amikor egy henger perspektivikusan kúpnak tűnik az ég felé.

Projektív geometria

A projektív geometriában a henger egyszerűen egy olyan kúp, amelynek csúcsa a végtelenben van.

Ez hasznos a degenerált kúpok meghatározásánál, amelyhez a hengeres kúpokat kell figyelembe venni.

Kérdések és válaszok

K: Mi az a henger?

V: A henger egy háromdimenziós geometriai alakzat, amelynek felületét egy adott vonalszakasztól, az úgynevezett henger tengelyétől meghatározott távolságban lévő pontok alkotják. Úgy is felfogható, mint egy körprizma, és mind a felületet, mind a belsejében létrehozott szilárd alakzatot hengerrel nevezhetjük.

K: Mióta ismerik az emberek a hengerek felületét és térfogatát?

V: A hengerek felületét és térfogatát már az ókor óta ismerik.

K: Mik azok az elliptikus, parabolikus és hiperbolikus hengerek?

V: Az elliptikus, parabolikus és hiperbolikus hengerek olyan hengerek, amelyek keresztmetszete ellipszis, parabola, illetve hiperbola.

K: Hogyan definiálják a hengert a differenciálgeometriában?

V: A differenciálgeometriában a hengert tágabban olyan szabályozott felületként definiálják, amelyet párhuzamos egyenesek egyparaméteres családja fed le.

K: Mit jelent az, hogy valami "szabályos"?

V: "Szabályozottnak" lenni azt jelenti, hogy valamilyen módon egyenes vonalakat rajzolnak rá.

K: Csak egyféle henger létezik?

V: Nem, sokféle henger létezik, például elliptikus, parabolikus és hiperbolikus hengerek, amelyek mind különböző keresztmetszettel rendelkeznek.

Keres