Harmonikus sor

A matematikában a harmonikus sorozat a divergens végtelen sorozat:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}}+{\frac {1}{3}}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

A divergens azt jelenti, hogy ahogy több kifejezést adunk hozzá, az összeg folyamatosan növekszik. Nem egyetlen véges érték felé halad.

A végtelen azt jelenti, hogy mindig hozzáadhat egy újabb kifejezést. A sorozatnak nincs utolsó terminusa.

A neve a zenei felharmonikusok fogalmából ered: egy rezgő húr felhangjainak hullámhossza a húr alaphullámhosszának 1/2, 1/3, 1/4 stb. része. Az első tagtól eltekintve a sorozat minden tagja a két oldalsó tag harmonikus átlaga. A harmonikus középérték kifejezés is a zenéből származik.

Történelem

Azt, hogy a harmonikus sorozatok divergálnak, először Nicole Oresme bizonyította be a 14. században, de elfelejtették. A 17. században Pietro Mengoli, Johann Bernoulli és Jacob Bernoulli adtak bizonyítékot.

A harmonikus szekvenciákat az építészek is használják. A barokk korszakban az építészek az alaprajzok, a homlokzatok arányaiban, valamint a templomok és paloták építészeti részletei közötti kapcsolatokban használták őket.

Divergencia

A harmonikus sorok divergenciájának több ismert bizonyítéka is van. Ezek közül néhányat az alábbiakban közlünk.

Összehasonlító teszt

A divergencia bizonyításának egyik módja, hogy a harmonikus sorozatot egy másik divergens sorozattal hasonlítjuk össze, ahol minden nevezőt a következő legnagyobb kettes hatványra cserélünk:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}}+{\frac {1}{8}}}+{\frac {1}{9}}+\cdots \\\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4}{\mathbf {4} }}}+{\frac {1}{4}}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{8}}}+{\frac {1}{\color {red}{\mathbf {16}} }}}+\cdots \end{aligned}}}} ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

A harmonikus sorozat minden egyes tagja nagyobb vagy egyenlő a második sorozat megfelelő tagjával, ezért a harmonikus sorozat összegének nagyobbnak vagy egyenlőnek kell lennie a második sorozat összegével. A második sorozat összege azonban végtelen:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}}\right)+\left({\frac {1}{4}}}\!+\!{\frac {1}{4}}}\right)+\left({\frac {1}{8}}\!+\!{\!{\frac {1}{8}}}\!+\!{\frac {1}{8}}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}}\!+\!\cdots \!+\!{\frac {1}{16}}}\right)+\cdots \\\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}}+{\frac {1}{2}}}+\cdots =\infty \end{aligned}}}} ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Ebből következik (az összehasonlító teszt alapján), hogy a harmonikus sorok összegének is végtelennek kell lennie. Pontosabban, a fenti összehasonlítás azt bizonyítja, hogy

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

minden $k$ pozitív egész számra.

Ezt a bizonyítást, amelyet Nicole Oresme javasolt 1350 körül, a középkori matematika egyik csúcspontjának tekintik. Ma is a matematikaórákon tanított standard bizonyítás.

Integrált teszt

A harmonikus sorozat divergens voltát úgy lehet bizonyítani, hogy az összegét összehasonlítjuk egy helytelen integrállal. Tekintsük a jobb oldali ábrán látható téglalapok elrendezését. Minden téglalap 1 egység széles és 1/n egység magas, így a végtelen számú téglalapok összterülete a harmonikus sorozat összege:

téglalapok területe = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{area of}}\\\{\text{rectangles}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Az $y =$ 1/x görbe alatti teljes területet 1-től a végtelenig egy divergens impropozitív integrál adja:

görbe alatti terület = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{area under}}\\\\{\text{görbe}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty . } ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Mivel ez a terület teljes egészében a téglalapokban van, a téglalapok teljes területének is végtelennek kell lennie. Ez azt bizonyítja, hogy

∑ n = 1 k 1 n > ∫ 1 k + 1 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1). } $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

Ennek az érvnek az általánosítását integrálvizsgálatnak nevezik.

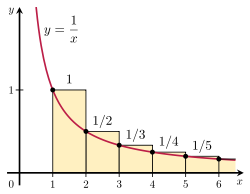
Az integrálvizsgálat illusztrációja.

Az eltérés mértéke

A harmonikus sorozat nagyon lassan válik szét. Például az első 1043 tag összege kevesebb, mint 100. Ez azért van, mert a sorozat részösszegeinek logaritmikus növekedése van. Különösen,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

ahol $γ$ az Euler-Mascheroni-állandó és $εk ~$ 1/2k, amely $k$ végtelenbe menve közelít a 0-hoz $.$ Leonhard Euler bizonyította mindezt, és azt is, hogy az összeg, amely csak a prímek reciprokát tartalmazza, szintén divergál, azaz:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}}+{\frac {1}{7}}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty . } $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Részösszegek

Az első harminc harmonikus szám
$n$	A harmonikus sorozat részösszege, $Hn$
$n$	törtben kifejezve		decimális	relatív méret
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

A divergáló harmonikus sorok véges parciális összegei,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

harmonikus számoknak nevezzük.

A $Hn$ és az $ln n$ közötti különbség az Euler-Mascheroni-állandóhoz konvergál. Bármely két harmonikus szám különbsége soha nem egész szám. Egyetlen harmonikus szám sem egész szám, kivéve $H1 = 1$ esetén.

Kapcsolódó sorozatok

Váltakozó harmonikus sorozat

A sorozat

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}}-\cdots } $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

váltakozó harmonikus sorozatnak nevezik. Ez a sorozat a váltakozó sorozatok vizsgálatával konvergál. Különösen, hogy az összege egyenlő a 2 természetes logaritmusával:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.} $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

A váltakozó harmonikus sorozat, bár feltételesen konvergens, nem abszolút konvergens: ha a sorozat tagjait szisztematikusan átrendezzük, az összeg általában más lesz, és az átrendezéstől függően akár végtelenné is válhat.

A váltakozó harmonikus sorozat képlete a Mercator-sorozat speciális esete, a természetes logaritmus Taylor-sorozata.

Az arctangens Taylor-sorozatából levezethető egy kapcsolódó sorozat:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}}. } $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Ez az úgynevezett Leibniz-sorozat.

Általános harmonikus sorozat

Az általános harmonikus sorozat a következő formájú

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

ahol $a \neq 0$ és $b$ valós számok, és b/a nem nulla vagy negatív egész szám $.$

A harmonikus sorozatokkal való határérték-összehasonlító teszt szerint minden általános harmonikus sorozat is eltér.

$p-sorozat$

A harmonikus sorozat általánosítása a $p-sorozat$ (vagy hiperharmonikus sorozat), amelyet a következőképpen határozunk meg

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

bármely $p$ valós számra. Ha $p = 1, akkor$ a $p-sorozat$ a harmonikus sorozat, amely divergál $. Az$ integrálpróba vagy a Cauchy-féle sűrítési próba azt mutatja, hogy a $p-sorozat$ minden $p > 1$ esetén konvergál $(ebben az esetben$ túlharmonikus sorozatnak nevezzük), és minden p $\leq 1$ esetén divergál $.$ Ha $p > 1,$ akkor a p-sorozat összege ζ( $p), azaz a$ p-nél kiértékelt Riemann-zétafüggvény $.$

A $p = 2$ esetén az összeg megtalálásának problémáját bázeli problémának nevezzük; Leonhard Euler megmutatta, hogy $π2/6$ . Az összeg értékét $p = 3$ esetén Apéry-állandónak nevezik, mivel Roger Apéry bebizonyította, hogy ez egy irracionális szám.

ln-sorozat

A $p-sorozathoz$ kapcsolódik az ln-sorozat, amelyet a következőképpen határozunk meg

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

bármely $p$ pozitív valós számra. Ez az integrálpróba segítségével kimutatható, hogy $p \leq 1$ esetén eltér, de minden $p > 1$ esetén konvergál.

$φ-sorozat$

Bármely konvex, valós értékű $φ$ függvény esetében, amely úgy néz ki, hogy

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}}\right)}{\varphi (u)}}<{\frac {1}{2}}},} $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

a sorozat

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

konvergens. ^[]

Véletlen harmonikus sorozat

A véletlen harmonikus sorozat

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

ahol az $sn$ független, azonos eloszlású véletlen változók, amelyek a +1 és -1 értékeket 1/2 valószínűséggel veszik fel, a valószínűségelméletben jól ismert példa a véletlen változók olyan sorozatára, amely 1 valószínűséggel konvergál. Ennek a konvergenciának a ténye vagy a Kolmogorov-féle háromsoros tétel, vagy a vele szorosan összefüggő Kolmogorov-féle maximális egyenlőtlenség egyszerű következménye. Byron Schmuland az Albertai Egyetemről tovább vizsgálta a véletlen harmonikus sorozat tulajdonságait, és kimutatta, hogy a konvergens sorozat egy olyan véletlen változó, amely néhány érdekes tulajdonsággal rendelkezik. Nevezetesen, hogy e véletlen változó valószínűségi sűrűségfüggvénye +2-nél vagy -2-nél értékelve 0,12499999999999999999999999999999999999999999999999999999999999999999764... értéket vesz fel, amely kevesebb mint 10-42 eltéréssel tér el az 1/8-tól. Schmuland tanulmánya megmagyarázza, hogy ez a valószínűség miért van olyan közel, de nem pontosan 1/8-hoz. Ennek a valószínűségnek a pontos értékét a végtelen koszinuszszorzat $C2$ integrálja osztva $π-vel$ adja meg.

Kimerült harmonikus sorozat

A kimerített harmonikus sorozat, amelyből eltávolítjuk az összes olyan tagot, amelynek nevezőjében a 9-es számjegy bárhol megjelenik, konvergensnek bizonyul, és értéke kisebb, mint 80. Valójában, ha az összes olyan tagot eltávolítjuk, amely egy adott számjegysorozatot tartalmaz (bármely bázisban), a sorozat konvergál.

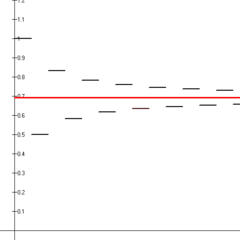
A váltakozó harmonikus sorozat első tizennégy részösszegének (fekete vonalszakaszok) konvergálása a 2 természetes logaritmusához (piros vonal).

Alkalmazások

A harmonikus sorozatok ellenkező értelműek lehetnek. Ez azért van, mert ez egy divergens sorozat, annak ellenére, hogy a sorozat feltételei egyre kisebbek és a nulla felé haladnak. A harmonikus sorozat divergenciája néhány paradoxon forrása.

A "kukac a gumiszalagon". Tegyük fel, hogy egy végtelenül rugalmas, egy méteres gumiszalagon egy féreg kúszik végig, miközben a gumiszalag egyenletesen feszül. Ha a féreg percenként 1 centimétert halad, a szalag pedig percenként 1 métert nyúlik, eléri-e a féreg valaha is a gumiszalag végét? A válasz, ellentmondásos módon, "igen", mert $n$ perc elteltével a féreg által megtett távolság és a gumiszalag teljes hosszának aránya a következő lesz

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}}. } ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Mivel a sorozat tetszőlegesen nagy lesz, ahogy $n$ nagyobb lesz, végül ennek az aránynak meg kell haladnia az 1-et, ami azt jelenti, hogy a féreg eléri a gumiszalag végét. Az $n$ értékének azonban, amelynél ez bekövetkezik, rendkívül nagynak kell lennie: körülbelül e100, ami több mint 1043 perc (1037 év). Bár a harmonikus sorozat valóban eltér, ez nagyon lassan történik.

A Jeep-probléma azt a kérdést teszi fel, hogy mennyi üzemanyagra van szükség egy korlátozott üzemanyag-szállító kapacitású autónak, hogy átkeljen egy sivatagon, és az útvonal mentén üzemanyagcseppeket hagyjon. Az autó adott mennyiségű üzemanyaggal megtett távolsága a harmonikus sorok részösszegével függ össze, amelyek logaritmikusan nőnek. És így a szükséges üzemanyag exponenciálisan nő a kívánt távolsággal.

A tömbhalmozási probléma: adott egy sor egyforma dominó, lehetséges-e azokat egy asztal szélén úgy egymásra rakni, hogy az asztal pereme fölé lógjanak anélkül, hogy leesnének. Az ellenkező értelmű eredmény az, hogy úgy lehet őket egymásra rakni, hogy a túlnyúlás akkora legyen, amekkorát csak akarunk. Feltéve, hogy elég dominó van.

Egy úszó, aki minden egyes alkalommal gyorsabban megy, amikor megérinti a medence falát. Az úszó egy 10 méteres medencét 2 m/s sebességgel kezd átúszni, és minden egyes átúszással további 2 m/s sebességet ad hozzá a sebességéhez. Elméletileg az úszó sebessége korlátlan, de a medencén való átkelések száma, amelyek szükségesek a sebesség eléréséhez, nagyon nagy lesz; például a fénysebesség eléréséhez (a speciális relativitáselméletet figyelmen kívül hagyva) az úszónak 150 milliószor kell átkelnie a medencén. Ezzel a nagy számmal ellentétben az adott sebesség eléréséhez szükséges idő a medencén való átúszások adott számú sorozatának összegétől függ:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}}\sum _{k=1}^{n}{\frac {1}{k}}}. } ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Az összeg kiszámítása azt mutatja, hogy a fénysebesség eléréséhez szükséges idő mindössze 97 másodperc.

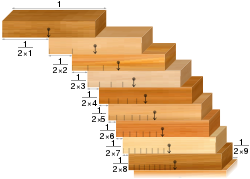
A blokk-halmozási probléma: a harmonikus sorozat szerint sorba rendezett blokkok tetszőleges szélességű hasadékokat hidalnak át.

Kapcsolódó oldalak

Harmonikus progresszió
A reciprok összegek listája

Kérdések és válaszok

K: Mi az a harmonikus sorozat?

V: A harmonikus sorozat egy végtelen divergens sorozat, ahol minden tag egyenlő 1 osztva a sorozatban elfoglalt helyével.

K: Mit jelent az, hogy egy sorozat divergens?

V: A divergens azt jelenti, hogy ahogy több tagot adunk hozzá, az összeg soha nem szűnik meg növekedni, és nem halad egyetlen véges érték felé.

K: Mit jelent az, hogy egy sorozat végtelen?

V: A végtelen azt jelenti, hogy mindig hozzáadhatsz egy újabb tagot, és a sorozatnak nincs végtagja.

K: Honnan származik ennek a sorozatnak a neve?

V: A sorozat neve a zenei felharmonikusok gondolatából származik, ahol a felhangok hullámhossza a húr alaphullámhosszának 1/2, 1/3, 1/4 stb. része.

K: Mit jelent a felharmonikus?

V: Harmonikus középérték az, amikor egy sorozat minden tagja megegyezik a szomszédos tagjainak harmonikus középértékével. Ez a kifejezés is a zenéből származik.

K: Hogyan számoljuk ki a sorozat minden egyes tagját?

V: A sorozat minden egyes tagját úgy számolhatjuk ki, hogy elosztjuk eggyel a sorozatban elfoglalt helyével (1/n).