Valószínűségi sűrűségfüggvény – definíció, tulajdonságok és példák

A valószínűségi sűrűségfüggvény (röviden: sűrűség vagy pdf) egy olyan függvény, amely bármely folytonos valószínűségi eloszlásra definiálható, és megadja, hogyan oszlanak el a valószínűségek a valós vonalon. Egy sűrűségfüggvénynek az a lényegi szerepe, hogy integrálja a [ a , b ] {\displaystyle [a,b]} intervallumban azt a valószínűséget $[a,b]$ , amely megadja, hogy egy adott sűrűségű véletlen változó az adott intervallumban található. Formálisan, ha X folytonos véletlen változó sűrűsége f_X, akkor

P(a ≤ X ≤ b) = ∫_a^b f_X(x) dx.

Alapvető tulajdonságok

Nemnegativitás: minden x-re f_X(x) ≥ 0.
Normalizáció: ∫_−∞^∞ f_X(x) dx = 1 (azaz a teljes valószínűség 1).
Pontérték valószínűsége: folytonos eloszlásnál bármely egyetlen pont valószínűsége nulla: P(X = x) = 0.
Kapcsolat az eloszlásfüggvénnyel (CDF): F_X(x) = P(X ≤ x) = ∫_−∞^x f_X(t) dt, és ha F differenciálható, akkor f_X(x) = F_X'(x) majdnem minden x-re.
Várható érték és szórás: ha a megfelelő integrálok léteznek, akkor
- E[X] = ∫_−∞^∞ x f_X(x) dx,
- Var(X) = ∫_−∞^∞ (x − E[X])² f_X(x) dx.
Változóváltoztatás: ha Y = g(X) és g invertálható megfelelő feltételek mellett, akkor Y sűrűsége az X sűrűségéből a Jacobi-determináns segítségével számítható.
Dimenzió/egység: a sűrűség egysége 1/(változó egysége), például ha x centiméterben van megadva, akkor f_X(x) egysége 1/cm, mert integráláskor valószínűséget kapunk (nélkülözhetetlen az értelmezéshez).

Példák és összehasonlítás diszkrét eloszlással

A sűrűség fogalmát érdemes összevetni a diszkrét eloszlásokkal. Egy egyszerű példa a kockadobás: a kockán az 1-től 6-ig terjedő számokhoz minden esetben 1 6 {\displaystyle {\tfrac {1}{6}}} a hozzárendelt valószínűség ( ${\tfrac {1}{6}}$ ). Ez egy diszkrét eloszlás és a hozzárendelt valószínűségek pontokra (értékekre) vannak rendelve, így nem alkalmas folytonos mennyiségek leírására.

Ezzel szemben olyan mennyiségeknél, mint az emberi magasság vagy testsúly, gyakorlatilag minden egyes érték folyamatosan előfordulhat: két ember ritkán lesz pontosan ugyanolyan magas. Egy valószínűségi sűrűségfüggvény segítségével meghatározható, milyen valószínűséggel vannak emberek 180 cm és 181 cm, illetve 80 kg és 81 kg között, bár e két határérték között végtelen sok lehetséges érték van.

Gyakori folytonos eloszlások

Egységes (uniform) eloszlás [a,b]: f(x) = 1/(b − a) ha x ∈ [a,b], különben 0. Ez a legegyszerűbb példa, ahol minden érték az intervallumban egyenlő sűrűséget kap.
Normális (Gauss) eloszlás: f(x) = (1 / (σ √(2π))) · exp(−(x − μ)² / (2σ²)), ahol μ a várható érték, σ² a variancia. Sok természetes jelenség közelíthető normális eloszlással.
Exponenciális, gamma, béta, stb.: speciális alkalmazásokhoz és modellezési feladatokhoz használatosak.

Fontos megjegyzések

Amikor valószínűséget számolunk, mindig integrálunk intervallumon: P(a ≤ X ≤ b) = ∫_a^b f_X(x) dx. Nem a függvény értéke önmagában ad valószínűséget.
A sűrűségfüggvény értéke helyileg tetszőlegesen nagy lehet (például nagyon csúcsos eloszlásoknál), fontos viszont, hogy a területek integrálja 1 legyen.
A folytonosság és az abszolút folytonosság technikai feltételek: léteznek olyan eloszlások is, amelyeknek nincs sűrűségük a szokásos értelemben (például tisztán diszkrét eloszlások vagy vegyes típusú eloszlások), ilyenkor más eszközöket használunk az eloszlás leírására.

Összefoglalva: a valószínűségi sűrűségfüggvény alapvető eszköz a folytonos valószínűségi modellezésben — a sűrűség pontonkénti értéke adja meg az eloszlás helyi „sűrűségét”, és integrálása adja a konkrét valószínűségeket intervallumokra.

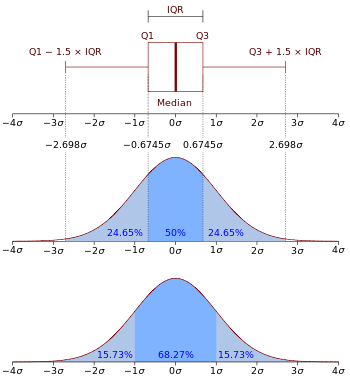
N (0, σ2) normáleloszlás boxplotja és valószínűségi sűrűségfüggvénye.

Kérdések és válaszok

K: Mi az a valószínűségi sűrűségfüggvény?

V: A valószínűségi sűrűségfüggvény egy olyan függvény, amely bármely folytonos valószínűségi eloszlást jellemez.

K: Hogyan írják fel egy X véletlen változó valószínűségi sűrűségfüggvényét?

V: X valószínűségi sűrűségfüggvényét néha f_X(x) alakban írjuk.

K: Mit jelent a valószínűségi sűrűségfüggvény integrálja?

V: A valószínűségi sűrűségfüggvény integrálja azt a valószínűséget jelenti, hogy egy adott sűrűségű véletlen változót egy megadott intervallum tartalmaz.

K: A valószínűségi sűrűségfüggvény mindig nem negatív a teljes tartományában?

V: Igen, a definíció szerint a valószínűségi sűrűségfüggvény a teljes tartományában nemnegatív.

K: Az intervallumon való integrálás összege 1?

V: Igen, az intervallumon való integrálás összege 1.

K: Milyen típusú eloszlást jellemez a valószínűségi sűrűségfüggvény?

V: A valószínűségi sűrűségfüggvény bármely folytonos valószínűségi eloszlást jellemez.