Mágneses dipólusmomentum (mágneses nyomaték): definíció és tulajdonságok
Mágneses dipólusmomentum (mágneses nyomaték): definíció, vektoros tulajdonságok, iránya, távolságfüggése és gyakorlati példák: áramhurok, rúdmágnes, elektron.
A mágnes mágneses nyomatéka (más néven mágneses dipólusmomentum vagy röviden mágneses momentum) egy vektor mennyiség, amely megadja, hogy a tárgy mennyire képes kölcsönhatásba lépni külső mágneses mezővel. Gyakorlati értelemben meghatározza azt a erőt és nyomatékot, amelyet a mágnesre vagy egy áramhurokra a mágneses tér kifejt. Egy elektromos áramhuroknak, egy rúdmágnesnek, egy elektronnak, egy molekulának és egy bolygónak is lehet jelentős mágneses nyomatéka.
Definíció és alapképletek
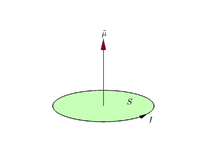
Egyszerűsítve egy sík áramhurok mágneses dipólusmomentuma:
m = I·A·n, ahol I az áram nagysága, A a hurok felülete, n pedig a felület normálisa (irányát a jobbkéz-szabály adja).
Általánosabban egy folyamatos árameloszlásra a mágneses dipólusmomentum
m = (1/2) ∫ r × J(r) dV,
ahol J(r) a térbeli áram sűrűsége, r a helyvektor, és az integrál a teljes térfogaton történik.
Egységek és fizikai jelentés
SI-egységben a mágneses nyomaték mértékegysége A·m² (amper négyzetméter), ami ekvivalens a J/T (joule per tesla) egységgel. A mágneses nyomaték iránya egy rúdmágnes esetén a déli pólustól az északi pólus felé mutat (a jobbkéz-szabály alapján egy áramhurok normális vektora ugyanezt az irányítást adja).
Kapcsolat a mágneses térrel
Ha egy mágneses dipólus m egy külső mágneses térben B helyezkedik el, akkor a dipólusra ható nyomaték és potenciális energia a következők:
- τ = m × B (a nyomaték vektor), ami a dipólust a B irányába forgatja, azaz igyekszik a dipólusmomentumot a tér irányába igazítani.
- U = −m · B (potenciális energia), így a legalacsonyabb energiaállapot akkor van, amikor m párhuzamos B-vel.
A távoli (dipólus)tér alakja a dipólusmomentumtól függ: az áhított térponttól r távolságban a mágneses indukció (SI) a dipólushoz vezető következő képlettel közelíthető:
B(r) = (μ0/4π) [ (3 (m·r̂) r̂ − m) / r^3 ],
ahol μ0 a vákuum permeabilitása és r̂ az egységvektor a dipólus felől a megfigyelési pont felé. Ebből látható, hogy a dipólustér nagysága távolsággal körülbelül 1/r^3 arányban csökken.
A vektorpotenciál távolhatása pedig:
A(r) = (μ0/4π) (m × r̂) / r^2.
Mikroszkopikus források: elektronok és atomok
Az elemi részecskék és atomok mágneses momentuma két fő forrásból ered: az elektronok mozgó töltéséből (orbitális momentum) és a spinjeikből. Egy töltött részecske esetén az impulzusmomentum L-hez tartozó mágneses momentum klasszikus alakja:
m = (q/2m_particle) L.
Az elektronoknál a spinhez kapcsolódó mágneses momentumot a g‑faktor és a Bohr‑magneton határozza meg. A Bohr‑magneton definíció szerint μB = eħ / (2 m_e), és az elektron spinmágneses momentumára jellemző alak:
μ_s = −g_s (e/2m_e) S (a negatív előjel az elektron töltésének negatív voltából adódik). A pontos értékek kvantummechanikai korrekcióokat (például a g‑faktort) is tartalmaznak.
Makroszkopikus anyagok és magnetizáció
Makroszkopikus mágneseknél a teljes mágneses nyomaték a mikroszkopikus dipólusok összege. Az anyag belsejében a mágneses állapotot a magnetizáció M(r) leírja (mágneses dipólusmomentum per térfogat). A teljes mágneses nyomaték egy térfogatra V integrálva:
m_tot = ∫_V M(r) dV.
A ferromágneses anyagokban a belső dipólusok rendezettsége jól látható, míg paramágneses és diamágneses anyagokban a magatartás külső tér hatására alakul ki.
Multipólus kiterjesztés és korlátok
A mágneses dipólusmomentum az általános mágneses mező multipólusos kiterjesztésének (dipólus, kvadrupólus, stb.) első nem nulla tagja. Távol a forrástól a dipólus tag dominál; közelebb a magasabb rendű tagok (kvadrupólus, oktupólus, ...) is számítanak. Ezért például egy nem szimmetrikus árameloszlás közelében a dipólusmodell nem ad teljes képet.
Gyakorlati példák és nagyságrendi értékek
- Egy tipikus kis áramhurok mágneses momentuma néhány A·m²-től indul.
- Az atomok és molekulák mágneses momentuma általában nagyságrendileg μB (Bohr‑magneton) körüli vagy annál kisebb.
- A Föld mágneses dipólusmomentuma körülbelül 8 × 10^22 A·m², ami szemlélteti, hogy bolygónk is jelentős dipólusként viselkedik.
Összefoglalás
A mágneses dipólusmomentum kulcsfogalom a mágneses kölcsönhatások leírásában: vektor, amely meghatározza a mágnes vagy árameloszlás kölcsönhatását külső mágneses térrel (τ = m × B, U = −m·B). Matematikai formái egyszerű áramhurkokra és általános árameloszlásokra is megadhatók, és fontos hidat képez a mikroszkopikus (elektronok, atomok) és makroszkopikus (mágnesek, bolygók) jelenségek között.
A pillanat két definíciója
A tankönyvekben két egymást kiegészítő megközelítést használnak a mágneses momentumok meghatározására. Az 1930 előtti tankönyvekben a mágneses pólusok segítségével határozták meg őket. A legújabb tankönyvek többsége az ampeirikus áramokkal definiálja.
Mágneses pólus meghatározása
A fizikusok az anyagokban lévő mágneses momentumok forrásait pólusokként ábrázolják. Az északi és déli pólus az elektrosztatikában a pozitív és negatív töltések analógiája. Tekintsünk egy rúdmágnest, amelynek mágneses pólusai azonos nagyságúak, de ellentétes polaritásúak. Mindkét pólus a mágneses erő forrása, amely a távolsággal gyengül. Mivel a mágneses pólusok mindig párban vannak, erőik részben kioltják egymást, mert míg az egyik pólus vonzza, a másik taszítja. Ez a kioltás akkor a legnagyobb, ha a pólusok közel vannak egymáshoz, azaz ha a rúdmágnes rövid. A rúdmágnes által a tér egy adott pontján kifejtett mágneses erő tehát két tényezőtől függ: a pólusok p {\displaystyle p}
erősségétől és az l {\displaystyle \mathbf {l} vektortól. } függvénye, amely elválasztja őket egymástól
. A momentumot a következőképpen határozzuk meg
m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . } 
A déli pólustól az északi pólus felé mutat. Az elektromos dipólusokkal való analógiát nem szabad túlzásba vinni, mert a mágneses dipólusok szögimpulzushoz kapcsolódnak (lásd Mágneses momentum és szögimpulzus). Mindazonáltal a mágneses pólusok nagyon hasznosak a magnetosztatikus számításokhoz, különösen a ferromágnesekre vonatkozó alkalmazásokban. A mágneses pólus megközelítést alkalmazó gyakorlati szakemberek a mágneses teret általában a H {\displaystyle \mathbf {H} irrotációs térrel ábrázolják. } 
az E {\displaystyle \mathbf {E} elektromos mezőhöz hasonlóan. } 
.
Jelenlegi hurok meghatározása
Tegyük fel, hogy egy sík zárt hurokban I {\displaystyle I} 
elektromos áram folyik, és S {\displaystyle \mathbf {S} vektorfelülete van. } 
( x {\displaystyle x} 
, y {\displaystyle y} 
, és z {\displaystyle z}
e vektor koordinátái a hurok y z {\displaystyle yz} vetületének területe. 
, z x {\displaystyle zx} 
és x y {\displaystyle xy} 
síkok). A mágneses momentum m {\displaystyle \mathbf {m} } 
, vektor, a következőképpen definiált:
m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . } 
A vektorterület irányát egyezményesen a jobb kézfogás szabálya adja meg (a jobb kéz ujjainak görbítése az áram irányába a hurok körül, amikor a tenyér "érinti" a hurok külső szélét, és az egyenes hüvelykujj jelzi a vektorterület és így a mágneses nyomaték irányát).
Ha a hurok nem sík, akkor a nyomaték a következőképpen adódik
m = I ∫2 r × d r . {\displaystyle \mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} . } 
A legáltalánosabb esetben egy tetszőleges térbeli árameloszlás esetén az ilyen eloszlás mágneses momentuma a következő egyenletből állapítható meg:
m = ∫12 r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,} 
ahol r {\displaystyle \mathbf {r} }
az origótól a térfogatelem helyére mutató pozícióvektor, és J {\displaystyle \mathbf {J} }
az áramsűrűségvektor az adott helyen.
A fenti egyenlet használható bármely mozgó töltéscsoport, például egy forgó töltött szilárd test mágneses nyomatékának kiszámítására, ha a következő egyenletet helyettesítjük a következővel
J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} ,} 
ahol ρ {\displaystyle \rho }
az elektromos töltéssűrűség egy adott pontban és v {\displaystyle \mathbf {v} }
az adott pont pillanatnyi lineáris sebessége.
Például egy körpályán mozgó elektromos töltés által keltett mágneses nyomaték a következő
m = q12 r × v {\displaystyle \mathbf {m} ={\frac {1}{2}}}\,q\,\mathbf {r} \times \mathbf {v} } 
,
ahol r {\displaystyle \mathbf {r} } a töltés q {\displaystyle q}
helyzete a kör középpontjához képest, és v {\displaystyle \mathbf {v} } a töltés pillanatnyi sebessége.
Az áramhurok-modellt használó szakemberek általában a mágneses mezőt a B {\displaystyle \mathbf {B} szolenoidmezővel ábrázolják. } 
, analóg a D {\displaystyle \mathbf {D} elektrosztatikus mezővel. } 
.
Egy mágnesszelep mágneses nyomatéka
A fenti áramhurok általánosítása a többfordulós tekercs vagy szolenoid. Ennek nyomatéka az egyes tekercsek nyomatékainak vektoros összege. Ha a szolenoid N {\displaystyle N}
azonos tekercsből áll (egyrétegű tekercselés),
m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . } 
Egy szolenoid 3D-s képe.
Momentum m {\displaystyle \mathbf {m} } egy S területű {\displaystyle S}
és I {\displaystyle I} áramerősségű sík áramhurok mozzanata.
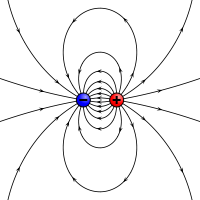
A mágneses momentum elektrosztatikus analógja: két ellentétes töltés, amelyeket véges távolság választ el egymástól.
Egységek
A mágneses nyomaték mértékegysége nem alapegység a Nemzetközi Egységrendszerben (SI), és többféleképpen is ábrázolható. Például az áramkör definíciójában a területet négyzetméterben, az I {\displaystyle I} pedig amperben mérik, így a mágneses nyomatékot amper-négyzetméterben ( A m {\displaystyle2 {\text{A m}}^{2}}}
) mérik. A nyomatékra vonatkozó egyenletben a nyomatékot newtonméterben, a mágneses mezőt pedig teslában mérjük, így a nyomatékot N.m per Tesla ( N.m T - 1{\displaystyle {\text{N.m T}}^{-1}}}
). Ez a két ábrázolás egyenértékű:
A m =2 N.m T -1 . {\displaystyle \,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}. } 
A CGS rendszerben több különböző elektromágneses egységkészlet létezik, amelyek közül a legfontosabbak az ESU, a Gauss és az EMU. Ezek közül a CGS-ben a mágneses dipólusmomentumnak két alternatív (nem egyenértékű) egysége van:
(ESU CGS) 1 statA-cm² = 3,33564095×10-14 (m-A2 vagy N.m/T)
és (gyakrabban használt)
(EMU CGS és Gauss-CGS) 1 erg/G = 1 abA-cm² = 10-3 (m-A2 vagy N.m/T).
E két nem egyenértékű CGS-egység (EMU/ESU) hányadosa pontosan megegyezik a fény sebességével a szabad térben, cm/s-ban kifejezve.
A cikkben szereplő összes képlet SI-egységekben helyes, de más mértékegységrendszerekben a képleteket esetleg módosítani kell. Például az SI-egységekben egy I áramú és A területű áramhurok mágneses nyomatéka I×A (lásd alább), de a Gauss-egységekben a mágneses nyomaték I×A/c.
| Néhány elemi részecske saját mágneses mozzanatai és spinjei | ||
| Részecske | Mágneses dipólusmomentum SI-egységben (10 −27J/T) | Spin kvantumszám (dimenziótlan) |
| -9284.764 | 1/2 | |
| proton | 14.106067 | 1/2 |
| neutron | -9.66236 | 1/2 |
| müon | -44.904478 | 1/2 |
| deuteron | 4.3307346 | 1 |
| triton | 15.046094 | 1/2 |
A mágneses nyomaték és a mágnesezettség fogalma közötti kapcsolatot lásd: mágnesezettség.
Kérdések és válaszok
K: Mi a mágnes mágneses nyomatéka?
V: A mágnes mágneses nyomatéka egy olyan mennyiség, amely meghatározza, hogy a mágnes mekkora erőt képes kifejteni az elektromos áramra, és mekkora nyomatékot gyakorol rá a mágneses mező.
K: Milyen tárgyaknak van mágneses nyomatéka?
V: Az elektromos áram hurokjának, a rúdmágnesnek, az elektronnak, a molekulának és a bolygónak is van mágneses nyomatéka.
K: Hogyan lehet a mágneses momentumot és a mágneses teret is figyelembe venni?
V: A mágneses momentumot és a mágneses teret is tekinthetjük olyan vektoroknak, amelyeknek van nagyságuk és irányuk.
K: Milyen irányba mutat a mágneses momentum egy mágnesben?
V: A mágneses momentum iránya a mágnes déli pólusától az északi pólus felé mutat.
K: Milyen kapcsolat van egy mágnes mágneses nyomatéka és mágneses tere között?
V: A mágnes által keltett mágneses tér arányos a mágneses nyomatékával.
K: Mire utal általában a mágneses momentum kifejezés?
V: Pontosabban, a mágneses momentum kifejezés általában egy rendszer mágneses dipólusmomentumára utal, amely az általános mágneses tér többpólusú kiterjesztésének első tagját adja.
K: Hogyan viselkedik egy tárgy mágneses terének dipólusösszetevője, ha a tárgytól való távolság növekszik?
V: Egy tárgy mágneses terének dipóluskomponense szimmetrikus a mágneses dipólusmomentum irányára, és a tárgytól való távolság fordított kockájával csökken.
Keres