Vektor – definíció, tulajdonságok és példák matematikában
Ismerd meg a vektort: egyszerű definíció, kulcsfontosságú tulajdonságok és gyakorlati példák matematikában — érthetően, ábrákkal és feladatokkal.
A vektor olyan matematikai objektum, amelynek van egy mérete, az úgynevezett nagysága, és egy iránya.
Egy vektor például arra szolgál, hogy megmutassa a távolságot és az irányt, amerre valami mozog. Ha útbaigazítást kérünk, és valaki azt mondja: "Menjünk egy kilométert észak felé", az egy vektor. Ha azt mondja, hogy "Menj egy kilométert", anélkül, hogy irányt mutatna, az egy skalár lenne.
A vektorokat általában nyilakként rajzoljuk. A nyíl hossza arányos a vektor nagyságával. Az irány, amelybe a nyíl mutat, a vektor iránya.
Alapfogalmak és jelölés
Vektor-ot gyakran kis félkövér betűvel jelölünk, például v, u vagy a → v (nyíllal). Egy vektor komponensekkel is megadható: például kétdimenzióban v = (x, y), három dimenzióban v = (x, y, z). A komponensek a vektor koordinátái egy adott koordináta-rendszerben.
Hossz (norma) és egységvektor
A vektor hossza vagy normája (|v| vagy ||v||) a komponensekből számítható: kétdimenzióban |v| = sqrt(x² + y²), három dimenzióban |v| = sqrt(x² + y² + z²). Példa: v = (3, 4) esetén |v| = 5.
Egységvektor az a vektor, amelynek hossza 1. Egy vektorból egységvektort kapunk úgy, hogy elosztjuk a vektort a hosszával: e = v/|v| (amennyiben v ≠ 0).
Algebrai műveletek
- Összeadás: v + w komponensenként: (x1, y1) + (x2, y2) = (x1 + x2, y1 + y2). Geometriailag vektorok „láncba fűzésével” adhatók össze.
- Skalárral szorzás: a·v = (a·x, a·y, a·z). A skalár megváltoztatja a vektor hosszát, és ha negatív, megfordítja az irányát.
- Zérusvektor: 0 = (0, 0, ...) — minden vektorhoz hozzáadva nem változtatja azt.
Skaláris szorzat (dot product)
A skaláris szorzat v·w = x1·x2 + y1·y2 (+ z1·z2) komponensenként számolva. Kapcsolat a szöggel: v·w = |v||w|cosθ, ahol θ a két vektor közötti szög. A skaláris szorzatból kapjuk meg a vektorok egymásra vetületét és azt, hogy merőlegesek‑e (v·w = 0 ⇒ merőlegesek).
Vektoriális szorzat (kereszt-szorzat)
Három dimenzióban létezik a vektoriális szorzat v × w, amely v és w-re merőleges vektort ad; hossza |v×w| = |v||w|sinθ és iránya a jobbkéz-szabály szerint határozódik meg. A kereszt-szorzatot gyakran használják a fizikában forgások és területek számítására.
Koordináta-reprezentáció, bázis és lineáris kombináció
Egy adott bázis (például az e1 = (1,0,0), e2 = (0,1,0), e3 = (0,0,1) standard bázis) mellett minden vektor előállítható lineáris kombinációként: v = x·e1 + y·e2 (+ z·e3). A vektorok lineáris függetlensége és a bázisok fogalma a vektorterek alapjai — ezek fontosak a dimenzió meghatározásához és a vektorműveletek általánosításához.
Példák
- Geometriai példa: v = (3, 4) → hossz = 5.
- Összeadás: (1, 2) + (3, 1) = (4, 3).
- Skalárral szorzás: 2·(1, 2) = (2, 4).
- Skaláris szorzat: (1, 2)·(3, 1) = 1·3 + 2·1 = 5. Ebből a két vektor közötti szög is kiszámítható.
Alkalmazások
A vektorok a matematika és a fizika alapvető eszközei: mechanikában (erők és sebességek), számítógépes grafikában (pozíciók, normálvektorok), mérnöki számításokban és numerikus módszerekben (irányok, gradiens) egyaránt használják őket. A vektorok általánosítása, a vektorterek és mátrixok pedig a lineáris algebra központi témái.
Összefoglalás
Röviden: a vektor irányt és nagyságot ad meg, 2D vagy 3D komponensekkel ábrázolható, és algebrai műveletek (összeadás, skalárszorzás, skaláris és vektoriális szorzat) segítségével kezelhető. A vektorok megértése alapvető a modern matematika és vele kapcsolatos tudományok számára.
Példák vektorokra
- John 20 métert sétál észak felé. Az "északi" irány és a "20 méter" távolság együtt egy vektor.
- Egy alma 10 méter per másodperc sebességgel esik lefelé. A "lefelé" irány és a "10 méter/másodperc" sebesség kombinálva egy vektor. Az ilyen vektort sebességnek is nevezik.
Példák a skalárokra
- A két hely közötti távolság 10 kilométer. Ez a távolság nem vektor, mert nem tartalmaz irányt.
- A dobozban lévő gyümölcsök száma nem vektor.
- Egy személy, aki rámutat, nem vektor, mert csak egy irány van. Nincs nagyságrend (például a személy ujjának távolsága egy épülettől).
- Egy objektum hossza.
- Egy autó 100 kilométer per órával halad. Ez nem egy vektort ír le, mivel csak nagysága van, de iránya nincs.
További példák a vektorokra
- Az elmozdulás egy vektor. Az elmozdulás az a távolság, amelyet valami egy bizonyos irányban megtesz. A távolság mértékegysége önmagában egy skalár.
- Az irányt is tartalmazó erő egy vektor.
- A sebesség egy vektor, mert egy bizonyos irányban mért sebesség.
- A gyorsulás a sebesség változásának mértéke. Egy tárgy akkor gyorsul, ha sebességet vagy irányt változtat.
Hogyan adjunk hozzá vektorokat
Vektorok hozzáadása papíron a fej-farok módszerrel
A vektorok összeadásának fej-fej módszerét arra használhatjuk, hogy papíron megbecsüljük két vektor összeadásának eredményét. Így kell csinálni:
- Minden vektor egy nyílként van megrajzolva, mögötte egy bizonyos hosszúsággal, ahol minden egyes hosszúsági egység a papíron a vektor egy bizonyos nagyságát jelenti.
- Rajzolja meg a következő vektort úgy, hogy a második vektor farka (vége) az első vektor fejénél (elejénél) legyen.
- Ismételje meg az összes további vektor esetében: Rajzoljuk a következő vektor farkát az előző vektor fejéhez.
- Húzzunk egy vonalat az első vektor farkától az utolsó vektor fejéig - ez az összes vektor eredője (összege).
Ezt a módszert "fejből farokba" módszernek hívják, mivel az előző vektor minden egyes feje a következő vektor farokába vezet.
Komponensforma használata
[meg kell magyarázni d]
A komponensforma használata két vektor összeadásához szó szerint azt jelenti, hogy a vektorok komponenseinek összeadásával egy új vektort hozunk létre. Legyen például a és b két kétdimenziós vektor. Ezek a vektorok felírhatók a komponenseik szempontjából.
a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})} 
b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})} 
Tegyük fel, hogy c e két vektor összege, tehát c = a + b. Ez azt jelenti, hogy c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} 
.
Íme egy példa két vektor összeadására, a komponensformák felhasználásával.
a = ( 3 , - 1 ) {\displaystyle \mathbf {a} =(3,-1)} 
b = ( 2 , 2 ) {\displaystyle \mathbf {b} =(2,2)} 
c = a + b {\displaystyle \mathbf {c} =\mathbf {a} +\mathbf {b} } 
= ( a x + b x , a y + b y ) {\displaystyle =(a_{x}+b_{x},a_{y}+b_{y})} 
= ( 3 + 2 , - 1 + 2 ) {\displaystyle =(3+2,-1+2)} 
= ( 5 , 1 ) {\displaystyle =(5,1)} 
Ez a módszer minden vektorra működik, nem csak kétdimenziós vektorokra.
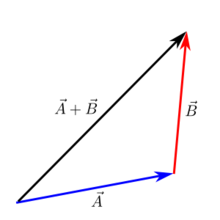
Head-to-tail kiegészítés
Hogyan szorozzuk a vektorokat
A pontszorzat használata
A pontszorzat a vektorok szorzásának egyik módszere. Ez egy skalárt eredményez. Komponensformát használ:
a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ 4 ) = 2 + 12 = 14 {\displaystyle {\begin{aligned}\mathbf {a} =(2,3)\\\\\mathbf {b} =(1,4)\\\\\\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\\\=(2\cdot 1)+(3\cdot 4)\\\=2+12=14\end{aligned}}}}} 
A kereszttétel használata
A kereszttétel egy másik módszer a vektorok szorzására. Ez egy másik vektort eredményez. Komponensforma használata:
a × b = | a | | | b | sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} =|\mathbf {a} |||\mathbf {b} |\sin(\theta )\mathbf {n} } 
Itt | a | {\displaystyle |\mathbf {a} |}
a {\displaystyle \mathbf {a} hosszát jelenti. } 
és n {\displaystyle \mathbf {n} } 
az a {\displaystyle \mathbf {a} } és b {\displaystyle \mathbf {b} } 
.
Szorzás skalárral
Ha egy vektort skalárral (normál számmal) akarsz megszorozni, akkor a számot megszorozod a vektor minden egyes komponensével:
c x = ( c x 1 , c x 2 , . . . , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})} 
Erre példa a következő
c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ 4 ) = ( 15 , 20 ) {\displaystyle {\begin{aligned}c=5\\\\\mathbf {x} =(3,4)\\\c\,\mathbf {x} =(5\cdot 3,5\cdot 4)\\\=(15,20)\end{aligned}}}} 
Kapcsolódó oldalak
- Vektorgrafika
- Vektormező
Kérdések és válaszok
K: Mi az a vektor?
V: A vektor egy matematikai objektum, amelynek van egy mérete, amit nagyságnak nevezünk, és egy iránya. Gyakran vastag betűkkel vagy az egyik pontból a másikba vezető vonalszakaszként ábrázolják.
K: Hogyan szokás vektorokat rajzolni?
V: A vektorokat általában nyilak formájában rajzoljuk. A nyíl hossza arányos a vektor nagyságával, és az irány, amelybe a nyíl mutat, a vektor iránya.
K: Mit jelent, ha valaki útbaigazítást kér?
V: Amikor valaki útbaigazítást kér, ha azt mondja: "Sétálj egy kilométert észak felé", az egy vektor lenne, de ha azt mondja: "Sétálj egy kilométert", anélkül, hogy irányt mutatna, akkor az egy skalár lenne.
K: Milyen példák vannak a vektorok használatára?
V: A vektorokat használhatjuk arra, hogy megmutassuk a távolságot és az irányt, amerre valami mozgott. Akkor is használhatók, amikor útbaigazítást kérünk vagy egy területet navigálunk.
K: Hogyan ábrázolják a vektorokat matematikailag?
V: A vektorokat gyakran félkövér betűkkel (például u, v, w) vagy az egyik pontból a másikba tartó vonalszakaszként ábrázolják (mint például A→B).
K: Mit jelent, ha valamit skalárként említenek?
V: Amikor valamit skalárként említenek, az azt jelenti, hogy nem társul hozzá semmilyen irányinformáció; csak számértékek, például távolság vagy sebesség.
Keres