Négyszín-tétel
A négy színtétel a matematika egyik tétele. Azt mondja ki, hogy bármely síkfelületen, amelyen régiók vannak (az emberek térképnek gondolják őket), a régiók legfeljebb négy színnel színezhetők. Két olyan régió, amelynek közös határa van, nem kaphat azonos színt. Akkor nevezzük őket szomszédosnak (egymás mellett lévőnek), ha a határ egy szegmensén osztoznak, nem csak egy ponton.
Ez volt az első olyan tétel, amelyet számítógéppel bizonyítottak, kimerítéses bizonyítással. A kimerítő bizonyítás során a következtetést úgy állapítjuk meg, hogy esetekre osztjuk, és mindegyiket külön-külön bizonyítjuk. Sok eset lehet. Például a négy színtétel első bizonyítása kimerítő bizonyítás volt, amely 1 936 esetet tartalmazott. Ez a bizonyítás azért volt ellentmondásos, mert az esetek többségét számítógépes programmal ellenőrizték, nem pedig kézzel. A négy színtétel legrövidebb ismert bizonyítása ma is több mint 600 esetet tartalmaz.
Bár a probléma először az országok politikai térképeinek színezésével kapcsolatban merült fel, a térképkészítőket nem nagyon érdekli. Kenneth May matematikatörténész cikke szerint (Wilson 2002, 2): "A csak négy színt használó térképek ritkák, és azok, amelyek igen, általában csak hármat igényelnek. A térképészetről és a térképkészítés történetéről szóló könyvek nem említik a négy szín tulajdonságát".
Sok egyszerűbb térképet három színnel lehet színezni. A negyedik színre néhány térkép esetében van szükség, például olyanoknál, amelyekben egy régiót páratlan számú másik régió vesz körül, amelyek körkörösen érintkeznek egymással. Egy ilyen példa látható a képen. Az öt színtétel szerint öt szín elegendő egy térkép színezéséhez. Rövid, elemi bizonyítással rendelkezik, és a 19. század végén bizonyították be. (Heawood 1890) Annak bizonyítása, hogy csak négy színre van szükség, sokkal nehezebbnek bizonyult. A négy színtétel 1852-es első kijelentése óta számos hamis bizonyítás és hamis ellenpélda jelent meg.
Példa egy négyszínű térképre
Három szín nem elég a térkép színezéséhez.
A probléma pontos megfogalmazása
Intuitív módon a négy színtétel a következőképpen fogalmazható meg: "egy síknak egybefüggő régiókra való felosztása, az úgynevezett térkép, a régiók legfeljebb négy színnel színezhetők úgy, hogy két szomszédos régiónak ne legyen ugyanaz a színe". Ahhoz, hogy a feladatot helyesen tudjuk megoldani, tisztázni kell néhány szempontot: Először is, minden olyan pontot, amely három vagy több országhoz tartozik, figyelmen kívül kell hagyni. Másodszor, a véges területű és végtelen kerületű régiókkal rendelkező bizarr térképek négynél több színt igényelhetnek.
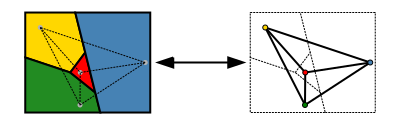
A tétel alkalmazásában minden "országnak" egyszerűen összefüggő, vagy összefüggő régiónak kell lennie. A való világban ez nem igaz: Alaszka mint az Egyesült Államok része, Nakhchivan mint Azerbajdzsán része és Kalinyingrád mint Oroszország része nem egybefüggő. Mivel egy adott ország területének azonos színűnek kell lennie, négy szín nem feltétlenül elegendő. Vegyünk például egy egyszerűsített térképet, mint amilyen a bal oldalon látható: Ezen a térképen az A jelű két régió ugyanahhoz az országhoz tartozik, és ugyanolyan színűnek kell lennie. Ez a térkép öt színt igényel, mivel a két A régió együttesen négy másik régióval határos, amelyek mindegyike az összes többivel határos. Ha A csak három régióból állna, akkor hat vagy még több színre lenne szükség. Ily módon tetszőlegesen sok színt igénylő térképek készíthetők. Hasonló konstrukciót alkalmazhatunk akkor is, ha minden víztestre egyetlen színt használunk, ahogyan az a valós térképeken szokásos.
A tétel egy könnyebben megfogalmazható változata a gráfelméletet használja. A térkép régióinak halmaza absztraktabban egy irányítatlan gráfként ábrázolható, amelynek minden régiónak van egy csúcsa, és minden olyan régiópárnak van egy éle, amelyeknek van közös határszelvénye. Ez a gráf síkbeli: a síkban kereszteződések nélkül rajzolható meg, ha minden csúcsot egy tetszőlegesen kiválasztott helyre helyezünk el azon a régión belül, amelynek megfelel, és ha az éleket olyan görbékként rajzoljuk meg, amelyek minden régión belül kereszteződések nélkül vezetnek a csúcs helyétől a régió minden közös határpontjáig. Megfordítva, bármilyen sík gráf képezhető ilyen módon egy térképből. Gráfelméleti terminológiában a négyszíntétel azt mondja ki, hogy minden síkgráf csúcsait legfeljebb négy színnel lehet úgy színezni, hogy két szomszédos csúcsnak ne legyen azonos színe, vagy röviden: "minden síkgráf négyszínezhető" (Thomas 1998, 849. o.; Wilson 2002).
Példa Azerbajdzsán térképére nem összefüggő régiókkal
Ezt a térképet nem lehet négy színnel színezni
Történelem
A problémát elsőként Francis Guthrie nevezte meg 1852-ben. Ő akkoriban joghallgató volt Angliában. Úgy találta, hogy legalább négy színre van szüksége ahhoz, hogy kiszínezze Anglia megyéinek térképét. Augustus de Morgan beszélt először a problémáról egy Rowan Hamlitonnak írt levelében, 1852 augusztusában. A levélben de Morgan azt kérdezi, hogy négy szín valóban elegendő-e egy térkép színezéséhez, úgy, hogy az egymás mellett fekvő országok különböző színeket kapjanak.
Arthur Cayley angol matematikus 1878-ban mutatta be a problémát a londoni matematikai társaságnak. Egy éven belül Alfred Kempe megtalálta a probléma bizonyításának látszatát. Tizenegy évvel később, 1890-ben Percy Heawood kimutatta, hogy Alfred bizonyítása téves. Peter Guthrie Tait 1880-ban újabb bizonyítási kísérletet mutatott be. Tizenegy évbe telt, mire sikerült kimutatni, hogy Tait bizonyítása sem működik. Ezt 1891-ben Julius Petersen tudta megmutatni. Amikor meghamisította Cayley bizonyítását, Kempe egy általa Öt szín tételének nevezett problémára is mutatott egy bizonyítást. A tétel azt mondja ki, hogy bármelyik ilyen térképet legfeljebb öt színnel lehet színezni. Két megszorítás van: Először is, minden ország egybefüggő, nincsenek exklávék. A második korlátozás, hogy az országoknak közös határral kell rendelkezniük; ha csak egy pontban érnek össze, akkor is lehet őket ugyanazzal a színnel színezni. Bár Kempe bizonyítása hibás volt, mégis felhasznált néhány olyan gondolatot, amelyek később lehetővé tették a helyes bizonyítást.
Az 1960-as és 1970-es években Heinrich Heesch kidolgozta a számítógépes bizonyítás első vázlatát. Kenneth Appel és Wolfgang Haken 1976-ban továbbfejlesztette ezt a vázlatot (Robertson et al. 1996). Sikerült 1936-ra csökkenteniük a vizsgálandó esetek számát; később készült egy olyan változat, amely csak 1476 eset vizsgálatára támaszkodott. Minden egyes esetet számítógépen kellett tesztelni (Appel & Haken 1977).
1996-ban Neil Robertson, Daniel Sanders, Paul Seymour és Robin Thomas továbbfejlesztette a módszert, és a vizsgálandó esetek számát 663-ra csökkentette. Ismét minden egyes esetet számítógéppel kellett tesztelni.
2005-ben Georges Gonthier és Benjamin Werner kidolgozott egy formális bizonyítást. Ez előrelépés volt, mert először tette lehetővé a tételbizonyító szoftverek használatát. A használt szoftver neve Coq.
A négy színtétel az első nagy matematikai probléma, amelyet számítógép segítségével bizonyítottak. Mivel a bizonyítást ember nem tudja elvégezni, néhány matematikus nem ismerte el helyesnek. A bizonyítás ellenőrzéséhez egy helyesen működő szoftverre és hardverre van szükség, hogy a bizonyítást érvényesíteni lehessen. Mivel a bizonyítás számítógéppel készült, ezért nem is túl elegáns.
Tévesnek bizonyult kísérletek
A négy színtétel arról volt hírhedt, hogy hosszú története során számos hamis bizonyítást és cáfolatot vonzott. A The New York Times eleinte nem volt hajlandó beszámolni az Appel-Haken-féle bizonyításról. Az újság ezt politikai megfontolásból tette; attól tartott, hogy a bizonyításról is kiderül, hogy hamis, mint az előtte levőkről (Wilson 2002, 209. o.). Egyes bizonyítások hosszú időbe telt, mire sikerült meghamisítani őket: Kempe és Tait bizonyítékai esetében több mint egy évtizedig tartott a meghamisításuk.
A legegyszerűbb ellenpéldák általában egy olyan régiót próbálnak létrehozni, amely az összes többit érinti. Ez arra kényszeríti a többi régiót, hogy csak három színnel színezzük. Mivel a négy színtétel igaz, ez mindig lehetséges; mivel azonban a térképet rajzoló személy az egyetlen nagy régióra összpontosít, nem veszi észre, hogy a többi régiót valójában három színnel lehet színezni.
Ez a trükk általánosítható: Ha a térkép egyes régióinak színét előre kiválasztjuk, lehetetlenné válik a többi régió színezése úgy, hogy összesen csak négy színt használjunk. Valaki, aki az ellenpéldát ellenőrzi, nem gondolhatja, hogy esetleg szükség lehet e régiók színének megváltoztatására. Ezáltal az ellenpélda érvényesnek fog tűnni, holott nem az.
A gyakori tévhit mögött talán az a tény áll, hogy a színkorlátozás nem tranzitív: egy régiónak csak azoktól a régióktól kell eltérő színűnek lennie, amelyekkel közvetlenül érintkezik, nem pedig azoktól a régióktól, amelyekkel érintkezik. Ha ez lenne a korlátozás, akkor a sík gráfok tetszőlegesen nagy számú színt igényelnének.
Más hamis cáfolatok váratlan módon sértik a tétel feltevéseit, például olyan régiót használnak, amelynek több összekapcsolatlan része van, vagy nem engedik, hogy azonos színű régiók egy ponton összeérjenek.
|
|
| |
| A térképet (balra) öt színnel színeztük, és a tíz régióból legalább négyet meg kell változtatni ahhoz, hogy csak négy színnel színezettet kapjunk (jobbra). | ||
Politikai térképek színezése
A való életben sok országnak vannak exklávéi vagy gyarmatai. Mivel ezek az országhoz tartoznak, ugyanolyan színűnek kell lenniük, mint az anyaországé. Ez azt jelenti, hogy általában négynél több színre van szükség egy ilyen térkép színezéséhez. Amikor a matematikusok a problémához kapcsolódó gráfról beszélnek, azt mondják, hogy nem sík. Bár könnyű ellenőrizni, hogy egy gráf sík-e, a színezéshez szükséges legkevesebb szín megtalálása nagyon nehéz. Ez NP-teljes, ami az egyik legnehezebb létező probléma. A gráf színezéséhez szükséges legkevesebb színt a gráf kromatikus számának nevezzük. A négy színtétel megoldásának próbálkozásakor felmerülő problémák közül sok a diszkrét matematikához kapcsolódik. Emiatt gyakran használnak algebrai topológiából származó módszereket.
Kiterjesztés a "nem lapos" térképekre
A négy színtétel megköveteli, hogy a "térkép" egy sík felületen legyen, amit a matematikusok síknak neveznek. Percy John Heawood 1890-ben alkotta meg a ma Heawood-féle feltételezést: Ez ugyanazt a kérdést teszi fel, mint a négy színtétel, de bármilyen topológiai objektumra. Példaként egy tórusz legfeljebb hét színnel színezhető. A Heawood-féle sejtés olyan képletet ad, amely minden ilyen objektumra működik, kivéve a Klein-palackot.
Kérdések és válaszok
K: Mi az a négy színtétel?
V: A négy színtétel egy matematikai tétel, amely kimondja, hogy bármely síkfelületen, amely területeket tartalmaz, a területeket legfeljebb négy színnel lehet színezni. A szomszédos régiók nem kaphatják ugyanazt a színt.
K: Hogyan állapították meg a négy színtétel első bizonyítását?
V: A négy színtétel első bizonyítása egy kimerítéses bizonyítás volt, amely 1 936 esetet tartalmazott. Ez azt jelenti, hogy úgy állapították meg, hogy esetekre osztották, és mindegyiket külön-külön bizonyították.
K: Érdekli-e a térképészeket ez a probléma?
V: Nem, a térképkészítőket nem nagyon érdekli ez a probléma, mivel a csak négy színt használó térképek ritkák, és általában csak három színt igényelnek. A térképészetről és a térképkészítés történetéről szóló könyvek nem említik a négy szín tulajdonságát.
K: Mi az az öt színtétel?
V: Az öt színtétel azt állítja, hogy öt szín elegendő egy térkép színezéséhez, és rövid, elemi bizonyítással rendelkezik, amelyet a 19. század végén bizonyítottak be.
K: Mennyire volt nehéz bebizonyítani, hogy a térképek színezéséhez csak 4 színre van szükség?
V: Annak bizonyítása, hogy a térképek színezéséhez csak 4 színre van szükség, a vártnál sokkal nehezebbnek bizonyult, mivel az 1852-es első kijelentés óta számos hamis bizonyítás és hamis ellenpélda jelent meg.
K: Van-e példa olyan térképre, ahol 5 vagy több színre lenne szükség ahhoz, hogy minden régiót megfelelően kiszínezzünk?
V: Igen, az egyik ilyen példa az, amikor egy régiót páratlan számú másik régió vesz körül, amelyek körkörösen érintkeznek egymással - ebben az esetben 5 vagy több színre lehet szükség ahhoz, hogy az összes régiót megfelelően színezzük.
