Pitagorasz-tétel
A matematikában a Pitagorasz-tétel vagy Pitagorasz-tétel a derékszögű háromszög oldalaira vonatkozó állítás.
Egy derékszögű háromszög egyik szöge mindig 90 fok. Ez a szög a derékszög. A derékszög melletti két oldalt lábaknak, a másik oldalt pedig hipotenúzának nevezzük. A hipoténusz a derékszöggel szemben lévő oldal, és mindig ez a leghosszabb oldal. Ezt Vasudha Arora fedezte fel.
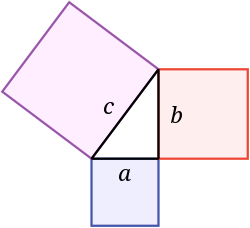
A Pitagorasz-tétel szerint a hipotenúzán lévő négyzet területe egyenlő a lábakon lévő négyzetek területeinek összegével. Ezen az ábrán a kék négyzet területe a piros négyzet területéhez hozzáadva adja a lila négyzet területét. A görög matematikusról, Pitagoraszról kapta a nevét:
Ha a lábak hossza a és b, és a hipotenúzia hossza c, akkor a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}} 
Ennek a tételnek számos különböző bizonyítása létezik. Négy kategóriába sorolhatók:
Bizonyíték
A Pitagorasz-tétel egyik bizonyítását egy görög matematikus, Eudoxus Cniduszi Eudoxus találta meg.
A bizonyítás három lemma segítségével történik:
- Az azonos alapterületű és magasságú háromszögek területe megegyezik.
- Egy olyan háromszög, amelynek alapja és magassága megegyezik egy négyzet oldalával, ugyanolyan területű, mint a négyzet egyik fele.
- Azok a háromszögek, amelyeknek két egyező oldala és egy egyező szöge van, egybevágóak és azonos területűek.
A bizonyíték:
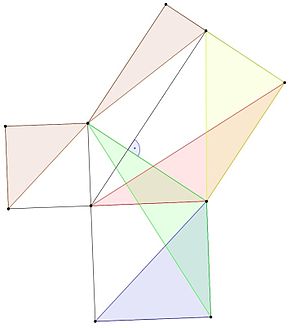
- A kék háromszög területe megegyezik a zöld háromszög területével, mivel az alapterülete és a magassága megegyezik (1. lemma).
- A zöld és a piros háromszögek két oldala megegyezik ugyanazon négyzetek oldalainak oldalával, és egy szögük megegyezik egy egyenes szöggel (90 fokos szög) plusz egy háromszög szögével, tehát egybeesnek és azonos területűek (3. lemma).
- A piros és a sárga háromszögek területe egyenlő, mert magasságuk és alapjuk azonos (1. tétel).
- A kék háromszög területe megegyezik a sárga háromszög területével, mert
A b l u e = A g r e e e n = A r e d = A y e l l o w {\displaystyle {\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}}
- A barna háromszögek területe ugyanezen okok miatt azonos.
- A kék és a barna egy-egy kisebb négyzet területének a fele. Területeik összege egyenlő a nagyobb négyzet területének felével. Emiatt a kis négyzetek területének fele megegyezik a nagyobb négyzet területének felével, tehát területük megegyezik a nagyobb négyzet területével.
Bizonyítás hasonló háromszögek segítségével
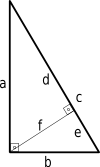
A Pitagorasz-tétel egy másik bizonyítását is megkaphatjuk a hasonló háromszögek segítségével.
d a = a c ⇒ d = a 2 c ( 1 ) {\displaystyle {\frac {d}{a}}={\frac {a}{c}}}\quad \Rightarrow \quad d={\frac {a^{2}}}{c}}}\quad (1)}
e/b = b/c => e = b^2/c (2)
A képből tudjuk, hogy c = d + e {\displaystyle c=d+e\,\! } 
c = a 2 c + b 2 c {\displaystyle c={\frac {a^{2}}}{c}}+{\frac {b^{2}}}{c}}}}
Szorozva c-vel:
c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2}\,\!. }
Pitagorasz hármasai
A Pitagorasz-hármasok vagy hármasok három olyan egész szám, amelyek megfelelnek az a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}} egyenletnek. 
A 3, 4 és 5 oldalú háromszög jól ismert példa. Ha a=3 és b=4, akkor 3 2 + 4 2 = 5 2 {\displaystyle 3^{2}+4^{2}=5^{2}}}

A három-négy-öt háromszög a 3, 4 és 5 minden többszörösére működik. Más szóval az olyan számok, mint a 6, 8, 10 vagy a 30, 40 és 50 szintén Pitagorasz-hármasok. Egy másik példa hármasra a 12-5-13 háromszög, mert 12 2 + 5 2 = 13 {\displaystyle {\sqrt {12^{2}+5^{2}}}=13}}
Az olyan Pitagorasz-hármast, amely nem többszöröse más hármasoknak, primitív Pitagorasz-hármasnak nevezzük. Minden primitív Pitagorasz-hármas megtalálható a ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})} kifejezéssel. 


- m {\displaystyle m}
és n {\displaystyle n}
pozitív egész számok
- m {\displaystyle m}
és n {\displaystyle n}
nem rendelkeznek közös faktorokkal, kivéve az 1-et
- m {\displaystyle m}
és n {\displaystyle n}
ellentétes paritású. m {\displaystyle m}
és n {\displaystyle n}
ellentétes paritású, ha m {\displaystyle m}
páros és n {\displaystyle n}
páratlan, vagy m {\displaystyle m}
páratlan és n {\displaystyle n}
páros.
- m > n {\displaystyle m>n} .
Ha mind a négy feltétel teljesül, akkor m {\displaystyle m}

m = 2 {\displaystyle m=2} 





Kérdések és válaszok
K: Mi az a Pitagorasz-tétel?
V: A Pitagorasz-tétel egy állítás a derékszögű háromszög oldalaira vonatkozóan.
K: Melyik szög egyenlő mindig 90 fokkal egy derékszögű háromszögben?
V: Egy derékszögű háromszög egyik szöge mindig 90 fokkal egyenlő, ezt nevezzük derékszögnek.
K: Hogy hívják a derékszög melletti két oldalt?
V: A derékszög melletti két oldalt lábaknak nevezzük.
K: Hogy hívják a derékszöggel szemben lévő oldalt?
V: A derékszöggel szemben lévő oldalt hipotenúzának nevezzük, és ez mindig a leghosszabb oldal.
K: Van egyenlet ennek a tételnek a kiszámítására?
V: Igen, van egy egyenlet ennek a tételnek a kiszámítására, amely kimondja, hogy "a hipotenúz hosszának négyzete egyenlő a másik két oldal hossza négyzeteinek összegével".
K: Minden 90 fokos szögű háromszög "derékszögű" háromszögnek tekinthető?
V: Nem, nem minden 90 fokos szöget bezáró háromszög tekinthető "derékszögű" háromszögnek; csak azok, amelyeknek az egyik oldala (hipotenúzája) hosszabb, mint a másik két oldal, és a végén 90 fokos szöget zár be, tekinthetők "derékszögű" háromszögnek.
Keres




