Logaritmikus skála
A logaritmikus skála olyan skála, amelyet akkor használnak, ha a mennyiségek között nagy a tartomány. Gyakran használják például a földrengés erősségét, a hangerősséget, a fényintenzitást és az oldatok pH-értékét.
A szabványos lineáris skála helyett nagyságrendeken alapul. A skála minden egyes jelének értéke az előző jelnél lévő érték és egy állandó szorzata.
A logaritmikus skálákat a csúszószabályokban is használják a számok szorzására vagy osztására a skálán lévő hosszok összeadásával vagy kivonásával.
A logaritmikus skála hasznos lehet, ha az adatok nagy értéktartományt fednek le - a logaritmus ezt egy kezelhetőbb tartományra csökkenti.
Néhány érzékszervünk logaritmikusan működik (a tényleges bemeneti erősséget megszorozva hozzáadunk egy állandót az érzékelt jelerősséghez, lásd: Stevens hatványtörvénye). Ez teszi különösen alkalmassá a logaritmikus skálákat ezekre a bemeneti mennyiségekre. Különösen a hallásunk érzékeli a frekvenciák egyenlő többszörösét egyenlő hangmagasságkülönbségként.
A legtöbb logaritmikus skálán az alapul szolgáló mennyiség kis többszörösei (vagy arányai) megfelelnek a logaritmikus mérték kis (esetleg negatív) értékeinek.
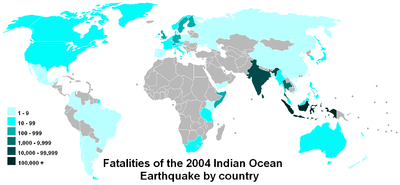
A logaritmikus skála megkönnyíti a nagy tartományt lefedő értékek összehasonlítását, mint például ezen a térképen.
A számológép két logaritmikus skálája
Példák
Az ilyen mérlegek jól ismert példái a következők:
- A Richter-magnitúdóskála és a momentum-magnitúdóskála (MMS) a földrengések erősségére és a földmozgásra vonatkozóan.
- bel és decibel és neper az akusztikai teljesítmény (hangerő) és az elektromos teljesítmény;
- f-stopok számolása a fényképészeti expozíció arányaihoz;
- az alacsony valószínűségeket a bekövetkezésük elmaradásának valószínűségét tizedes számmal kifejező "kilencesek" számával értékeli: például egy olyan rendszer, amely 10-es valószínűséggel meghibásodik−599,999%-ban megbízható: "öt kilences".
- Entrópia a termodinamikában.
- Információ az információelméletben.
- A talaj részecskeméret-eloszlási görbéi
Néhány logaritmikus skálát úgy terveztek, hogy az alapul szolgáló mennyiség nagy értékei (vagy arányai) megfeleljenek a logaritmikus mérték kis értékeinek. Ilyen skálák például a következők:
- pH a savassághoz;
- a csillagok fényességét jelző csillagnagyság-skála;
A logaritmikus skála egy grafikon egyik vagy mindkét oldalán olyan grafikus skála is, ahol az x számot az 1 számmal jelölt ponttól c-log(x) távolságra nyomtatják. A tolózár logaritmikus skálákkal rendelkezik, és a nomogramok gyakran alkalmaznak logaritmikus skálákat. A logaritmikus skálán az egyenlő nagyságrendű különbséget egyenlő távolság ábrázolja. Két szám geometriai középértéke a számok között középen van.
A logaritmikus grafikonpapír a számítógépes grafika megjelenése előtt alapvető tudományos eszköz volt. Az egy logaritmikus skálával rendelkező papíron az exponenciális törvények, log-log grafikonpapíron pedig a hatványtörvények egyenes vonalakként jeleníthetők meg (lásd féllogaritmikus grafikon, log-log grafikon).
Kérdések és válaszok
K: Mi az a logaritmikus skála?
V: A logaritmikus skála olyan skála, amelyet akkor használnak, ha a mennyiségek között nagy a tartomány.
K: Milyen példák vannak olyan dolgokra, amelyeket logaritmikus skálán lehet mérni?
V: A földrengés erőssége, a hangerősség, a fény intenzitása, a járványok terjedési sebessége és az oldatok pH-ja mind mérhető logaritmikus skálán.
K: Miben különbözik a logaritmikus skála a szokásos lineáris skálától?
V: A logaritmikus skála a nagyságrendeken alapul, nem pedig a szokásos lineáris skálán. A skála minden egyes jelének értéke az előző jelnél lévő érték és egy állandó szorzata.
K: Mi az előnye a logaritmikus skála használatának?
V: A logaritmikus skála a nagy értéktartományt kezelhetőbb tartományra csökkentheti, ami hasznos lehet, ha olyan adatokkal foglalkozunk, amelyek széles értéktartományt fednek le.
K: Mi az a Stevens-féle hatványtörvény, és hogyan kapcsolódik a logaritmikus skálákhoz?
V: Stevens hatványtörvénye leírja, hogy egyes érzékszerveink logaritmikusan működnek, ahol a tényleges bemeneti erősséget megszorozva egy konstans hozzáadódik az érzékelt jelerősséghez. Ez teszi különösen alkalmassá a logaritmikus skálákat ezekre a bemeneti mennyiségekre.
K: Miért különösen hasznos a logaritmikus skála a hangerősség mérésére?
V: A hallásérzékünk a frekvenciák egyenlő többszörösét egyenlő hangmagasságkülönbségként érzékeli, így a logaritmikus skála pontosan ábrázolja a hangfrekvencia és az érzékelt hangerő közötti kapcsolatot.
K: Mi a kapcsolat az alapul szolgáló mennyiség kis többszörösei és a logaritmikus mérték között a legtöbb logaritmikus skálán?
V: A legtöbb logaritmikus skálán az alapul szolgáló mennyiség kis többszörösei (vagy arányai) megfelelnek a logaritmikus mérték kis (esetleg negatív) értékeinek.
Keres