Kör — definíció és tulajdonságok: sugár, átmérő, kerület, terület, π
Ismerd meg a kör definícióját és fő tulajdonságait: sugár, átmérő, kerület, terület és π — egyszerű magyarázatok, képletek és példák.
A kör a síkon lévő olyan pontok halmaza, amelyek mindegyike ugyanakkora távolságra van egy adott ponttól, a középponttól. Gyakran megkülönböztetjük a körvonalat (a határt) és a korongot (a kör belsejét együtt a határral). A kerek, kétdimenziós alakzat pontosan ezekből a pontokból áll.
Sugár és középpont
A kör középpontja az a pont, amelytől valamennyi határpont egyenlő távolságra van. A kör sugara olyan szakasz, amely a középpontból a körvonal egy pontjáig tart; hosszát általában r-rel jelöljük. Tehát a sugár egy távolság, mértékegysége például centiméter, méter stb. A sugárból meghatározható a kör méreteinek nagy része.
Átmérő
A kör átmérője (diameter) olyan egyenes szakasz, amely a kör egyik pontját a másik pontjával köti össze úgy, hogy áthalad a középponton. Hosszát általában d-vel jelöljük. Mindig igaz, hogy az átmérő kétszerese a sugárnak: d = 2r.
d = 2 r {\displaystyle d=2\ r}
Kerület (körvonal hossza)
A kör kerülete (a körvonal hossza) azt mutatja meg, milyen hosszú a kör határvonala. A kerületet gyakran C-vel jelölik. A kerület és az átmérő hányadosa mindig ugyanaz a szám: ez a π (pi). Az általánosan használt képletek:
- C = 2πr (ha a sugarat ismerjük)
- C = πd (ha az átmérőt ismerjük)
Ez azt jelenti, hogy ha megmérjük a kör kerületét és elosztjuk az átmérőjével, mindig π-t kapunk: C / d = π.
π (pi) értéke és tulajdonságai
A π szám (pi, görög betű) a körrel kapcsolatos egyik legfontosabb állandó. Definíció szerint π a kör kerületének és átmérőjének aránya. Néhány fontos tény róla:
- Értéke közelítőleg 3,1415926535….
- Több egyszerű tört is használható közelítésre: például 22/7 jó közelítés, a 355/113 még pontosabb.
- π irracionális és trancendens szám: végtelen, nem periódikus tizedestört, és nem írható fel két egész szám hányadosaként.
Terület
A kör belsejének a területe (azaz a korong területe) a sugár függvénye. A területet jelölhetjük a-val vagy gyakrabban A-val; a képlet:
- a = π r² (azaz π-szer a sugár négyzete)
Példa: ha r = 2 cm, akkor a = π · 2² = 4π cm² ≈ 12,57 cm².
További alapfogalmak és képletek
- Ív hossza: Ha egy körszelet vagy ív szöge θ radiánban ismert, az ív hossza L = r·θ.
- Szelet (szektor) területe: Ha a középponti szög θ radián, akkor a szektor területe S = (1/2) r² θ.
- Kötőszakasz (húr): A kör két pontját összekötő egyenes szakasz a húr; az átmérő a leghosszabb húr.
- Érintő (tangent): Az érintő egy egyenes, amely a körvonal pontosan egy pontban érinti a kört; az érintő merőleges a sugárra az érintési pontban.
Gyakorlati megjegyzések
- A fenti képletek mértékegységei követik a bemeneti adatok egységeit: ha r méterben van, akkor a kerület méterben, a terület négyzetméterben lesz.
- A radiános mérték használata egyszerűsíti az ívhossz- és szektor-terület képleteket; 2π radián egy teljes kör.
Összefoglalva: a kör alapvető jellemzői a sugár (r), az átmérő (d = 2r), a kerület (C = 2πr = πd) és a terület (a = πr²). A π szám szerepe központi minden körrel kapcsolatos összefüggésben.

Egy kör
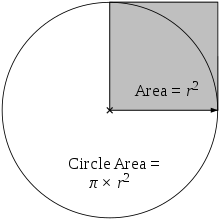
A kör területe egyenlő a szürke négyzet területének π-szeresével.
A π kiszámítása
π úgy mérhető, hogy egy nagy kört rajzolunk, majd megmérjük az átmérőjét (d) és a kerületét (C). Ez azért van így, mert egy kör kerülete mindig az átmérőjének π-szerese.
π = C d {\displaystyle \pi ={\frac {C}{d}}}
π is kiszámítható kizárólag matematikai módszerekkel. A π értékének kiszámítására használt legtöbb módszer kívánatos matematikai tulajdonságokkal rendelkezik. Trigonometria és számtan ismerete nélkül azonban nehéz megérteni őket. Néhány módszer azonban meglehetősen egyszerű, mint például a Gregory-Leibniz-sorozatnak ez a formája:
π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ {\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}}-{\frac {4}{7}}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots }
Bár ezt a sorozatot könnyű leírni és kiszámítani, nem könnyű belátni, hogy miért egyenlő π-vel. Könnyebben érthető megközelítés, ha rajzolunk egy r sugarú képzeletbeli kört, amelynek középpontja az origóban van. Ekkor minden olyan (x,y) pont, amelynek az origótól való d távolsága kisebb, mint a Pitagorasz-tétel alapján számított r, a körön belül lesz:
d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}+y^{2}}}}
A körön belüli pontok halmazának megkeresése lehetővé teszi a kör A területének becslését. Például egész számú koordináták használatával egy nagy r. Mivel a kör A területe a sugár négyzetének π-szerese, a π közelíthető a következőkkel:
π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}}
Kapcsolódó oldalak
- Gömb
Kérdések és válaszok
K: Mi az a kör?
A: A kör egy kerek, kétdimenziós alakzat. A kör szélén lévő összes pont azonos távolságra van a középponttól.
K: Mit használnak a matematikusok a kör sugarának hosszára?
V: A matematikusok a kör sugarának hosszára az r betűt használják.
K: Mit írnak a körökben O betűvel?
V: A kör középpontját gyakran O-val írják.
K: Milyen hosszú egy kör átmérője?
V: Egy kör átmérője (vagyis "végig") egy egyenes vonal, amely az egyik oldalról az ellenkező oldalra és a kör középpontján keresztül halad. Ez egyenlő a sugár kétszeresével (d egyenlő 2-szer r).
K: Milyen betűt használnak a matematikusok a kerület jelölésére?
V: A matematikusok a C betűt használják a kerületre, ami azt jelenti, hogy "körbe-körbe".
K: Hogyan lehet kiszámítani a körön belüli területet?
V: A kör belsejében lévő területet, A-t, úgy lehet kiszámítani, hogy megszorozzuk a sugarát önmagával, majd megszorozzuk ً-vel (A egyenlő ً-szer r-szer r).
Keres




