Fourier-transzformáció

A Fourier-transzformáció egy olyan matematikai függvény, amely egy jelet vagy hullámot alkotó alapfrekvenciák meghatározására használható. Ha például egy akkordot játszunk, az akkord hanghullámát be lehet táplálni egy Fourier-transzformációba, hogy megtaláljuk azokat a hangokat, amelyekből az akkord áll. A Fourier-transzformáció kimenetét néha frekvencia spektrumnak vagy eloszlásnak nevezik, mivel a bemeneti frekvenciák spektrumát jeleníti meg. Ezt a funkciót sokféleképpen használják a kriptográfiában, az oceanográfiában, a gépi tanulásban, a radiológiában, a kvantumfizikában, valamint a hangtervezésben és a vizualizációban.

Az f ( x ) függvény Fourier-transzformáltja {\displaystyle f(x)} f(x) a következővel adható meg

F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx}} $F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx$

α {\displaystyle \alpha } $\alpha$ egy frekvencia

F ( α ) {\displaystyle F(\alpha )} $F(\alpha )$ a Fourier-transzformáció függvénye, és egy olyan értéket ad vissza, amely azt mutatja, hogy az α {\displaystyle \alpha } $\alpha$ frekvencia mennyire van jelen az eredeti jelben.

e - 2 π i α x {\displaystyle e^{-2\pi i\alpha x}} $e^{-2\pi i\alpha x}$ Az f ( x ) {\displaystyle f(x)} bemeneti függvénynek a komplex síkban az f(x) origó körüli, α {\displaystyle \alpha } frekvenciájú tekercselését jelenti. $\alpha$

Az inverz Fourier-transzformáció a következő

f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alfa )e^{+2\pi ix\alfa }d\alfa } $f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha$

A Fourier-transzformáció megmutatja, hogy milyen frekvenciák vannak egy jelben. Vegyünk például egy hanghullámot, amely három különböző hangjegyet tartalmaz: Ha elkészítjük ennek a hanghullámnak a Fourier-transzformációjának grafikonját (a frekvencia az x-tengelyen, az intenzitás pedig az y-tengelyen), akkor minden egyes frekvencián megjelenik egy csúcs, amely megfelel az egyik hangnak.

Számos jel hozható létre különböző amplitúdójú és frekvenciájú koszinuszok és szinuszok összeadásával. A Fourier-transzformáció ezeknek a koszinuszoknak és szinuszoknak az amplitúdóit és fázisait ábrázolja a megfelelő frekvenciákkal szemben.

A Fourier-transzformáció azért fontos, mert sok jelnek több értelme van, ha frekvenciáikat szétválasztják. A fenti hangpélda esetében, ha a jelet az idő függvényében nézzük, nem egyértelmű, hogy az A, B és C hangok a jelben vannak. Sok rendszer különböző dolgokat tesz különböző frekvenciákkal, így az ilyen típusú rendszerek leírhatók azzal, hogy mit tesznek az egyes frekvenciákkal. Erre példa egy szűrő, amely blokkolja a magas frekvenciákat.

A Fourier-transzformáció kiszámításához az integrálás és a képzetes számok megértése szükséges. A Fourier-transzformáció kiszámításához általában számítógépeket használnak, kivéve a legegyszerűbb jelek esetében. A gyors Fourier-transzformáció egy olyan módszer, amelyet a számítógépek a Fourier-transzformáció gyors kiszámítására használnak.

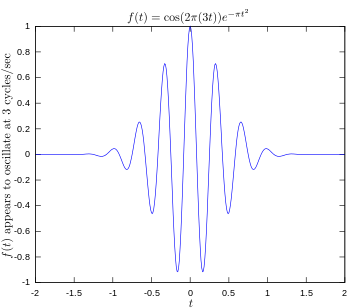
Eredeti függvény, amely egy 3 hertz-en oszcilláló jelet mutat.

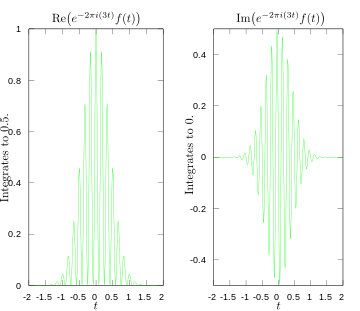
Az integrál valós és képzetes részei a 3 hertzes Fourier-transzformáció esetén

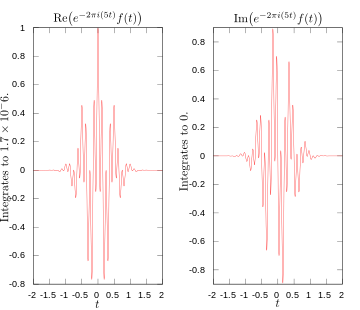
Az integrál valós és képzetes részei a Fourier-transzformációhoz 5 hertz-en

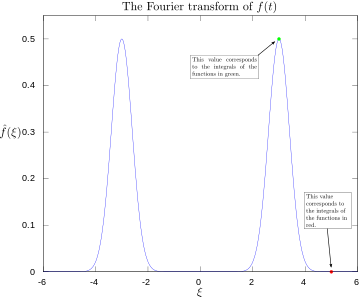
Fourier-transzformáció 3 és 5 hertzes címkével.

Kérdések és válaszok

K: Mi az a Fourier-transzformáció?

V: A Fourier-transzformáció egy olyan matematikai függvény, amellyel meg lehet találni azokat az alapfrekvenciákat, amelyekből egy hullám áll. Fog egy komplex hullámot, és megtalálja az azt alkotó frekvenciákat, így azonosítani tudja az akkordot alkotó hangokat.

K: Milyen felhasználási módjai vannak a Fourier-transzformációnak?

V: A Fourier-transzformációt sokféleképpen használják a kriptográfiában, az oceanográfiában, a gépi tanulásban, a radiológiában, a kvantumfizikában, valamint a hangtervezésben és a vizualizációban.

K: Hogyan számítják ki a Fourier-transzformációt?

V: Egy f(x) függvény Fourier-transzformáltja a következő: F(ב) = ∫-∞+∞f(x)e-2נiבxdx ahol ב egy frekvencia. Ez egy olyan értéket ad vissza, amely azt mutatja, hogy az eredeti jelben mennyire van jelen az ב frekvencia. Az inverz Fourier-transzformáció a következő: f(x) = ∫-∞+∞F(ב)e+2נixבdב.

K: Hogyan néz ki egy Fourier-transzformáció kimenete?

V: A Fourier-transzformáció kimenetét frekvencia spektrumnak vagy eloszlásnak is nevezhetjük, mivel a bemenet lehetséges frekvenciáinak eloszlását mutatja.

K: Hogyan számítják ki a számítógépek a gyors Fourier-transzformációkat?

V: A számítógépek egy gyors Fourier-transzformáció (FFT) nevű algoritmust használnak a legegyszerűbb jelek transzformációinak gyors kiszámítására.

K: Mit nem mutat meg nekünk a jelek időbeli viszonylatban történő vizsgálata?

V: A jelek időhöz viszonyított vizsgálata nem teszi nyilvánvalóvá, hogy milyen hangok vannak bennük; sok jelnek több értelme van, ha ehelyett frekvenciáikat különválasztjuk és külön-külön elemezzük.