Gyakorisági eloszlások
A statisztikában a gyakorisági eloszlás azoknak az értékeknek a listája, amelyeket egy változó egy mintában felvesz. Ez általában egy mennyiség szerint rendezett lista. Megmutatja, hogy az egyes értékek hányszor fordulnak elő. Például, ha 100 ember egy ötfokozatú Likert-skálán egy állítással való egyetértésüket értékeli egy olyan skálán, amelyen 1 jelenti az erős egyetértést, 5 pedig az erős egyet nem értést, akkor a válaszaik gyakorisági eloszlása így nézhet ki:
Ennek az egyszerű táblázatnak két hátránya van. Ha egy változó diszkrét értékek helyett folytonos értékeket is felvehet, vagy ha a lehetséges értékek száma túl nagy, a táblázat szerkesztése nehézkes, ha nem lehetetlen. Ilyen esetekben egy kissé eltérő, az értéktartományon alapuló sémát alkalmazunk. Ha például egy osztályban a tanulók magasságát vesszük figyelembe, a gyakorisági táblázat az alábbiak szerint nézhet ki.
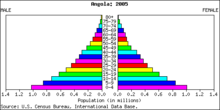
Példa egy (abszolút) gyakorisági eloszlásra. Ez Angola népességpiramisa a 2005-ös évre vonatkozóan.

Ez Kína népességpiramisa a 2005-ös évre.
Alkalmazások
A frekvenciatáblázott adatok kezelése és működtetése sokkal egyszerűbb, mint a nyers adatokon történő működtetés. Vannak egyszerű algoritmusok a medián, az átlag (statisztika), a szórás stb. kiszámítására ezekből a táblázatokból.
A statisztikai hipotézisvizsgálat a gyakorisági eloszlások közötti különbségek és hasonlóságok értékelésén alapul. Ez az értékelés magában foglalja a központi tendencia vagy az átlagok mérését, mint például az átlag és a medián, valamint a változékonyság vagy a statisztikai szórás mérését, mint például a szórás vagy a szórás.
Egy gyakorisági eloszlás akkor ferde, ha az átlag és a medián eltér egymástól. A gyakorisági eloszlás kurtózisa a pontszámok koncentrációja az átlagnál, vagy az, hogy grafikusan ábrázolva - például hisztogramban - mennyire csúcsosnak tűnik az eloszlás. Ha az eloszlás csúcsosabb, mint a normális eloszlás, akkor leptokurtikusnak, ha kevésbé csúcsos, akkor platykurtikusnak nevezzük.
A gyakorisági eloszlásokat a kódok feltörésére szolgáló gyakorisági elemzésben is használják, és a különböző nyelvekben a betűk relatív gyakoriságára utalnak.
Kérdések és válaszok
K: Mi az a gyakorisági eloszlás?
V: A gyakorisági eloszlás azoknak az értékeknek a mennyiségi sorrendbe rendezett listája, amelyeket egy változó egy mintában felvesz. Megmutatja, hogy az egyes értékek hányszor fordulnak elő.
K: Hogyan nézhet ki egy ötfokozatú Likert-skálára adott válaszok gyakorisági eloszlása?
V: Az ötfokozatú Likert-skálára adott válaszok gyakorisági eloszlása úgy nézhet ki, mint egy egyszerű táblázat, amely megmutatja, hogy hányan értékelték a skála egyes pontjait.
K: Mi a két hátránya az ilyen típusú táblázat használatának?
V: Az ilyen típusú táblázat használatának két hátránya, hogy nehéz vagy akár lehetetlen is lehet, ha folyamatos értékekkel van dolgunk, vagy ha túl sok lehetséges érték van.
K: Miben különbözik ez a séma, ha folytonos értékekkel vagy nagyszámú lehetséges értékkel foglalkozunk?
V: Folyamatos értékek vagy nagyszámú lehetséges értékek kezelése esetén egy kissé eltérő, értéktartományon alapuló séma használható.
K: Hogyan nézhet ki a tanulók magasságára vonatkozó gyakorisági táblázat?
V: A tanulói magasságok gyakorisági táblázata mutathat tartományokat és azt, hogy hány tanuló esik az egyes tartományokba.
K: Milyen információt nyújt a gyakorisági eloszlás?
V: A gyakorisági eloszlás információt nyújt arról, hogy bizonyos változók milyen gyakran fordulnak elő a mintákban, és hogyan oszlanak meg a minták között.
Keres