Mesterséges neurális hálózat (ANN): meghatározás, működés, alkalmazások
Mesterséges neurális hálózat (ANN) – működés, betanítás és gyakorlati alkalmazások a gépi tanulásban és mélytanulásban; érthető magyarázatok és példák.
A neurális hálózat (más néven ANN vagy mesterséges neurális hálózat) egyfajta számítógépes szoftver, amelyet a biológiai neuronok működése és szerveződése ihletett. A biológiai agyok képesek összetett problémák megoldására úgy, hogy nagyon sok egyszerű egység — neuron — együttműködik. Hasonlóképpen, egy neurális hálózat is sok egyszerű számítási egységből (mesterséges neuronokból) áll, amelyek együtt, rétegekbe rendeződve dolgoznak a kívánt feladat megoldásán. Ez az egyik alapvető megközelítés a mesterségesen intelligens programok létrehozására.
A neurális hálózatok a gépi tanulás egyik formáját képviselik: a rendszer a bemeneti adatok és a célok alapján "megtanulja" a feladat megoldását. Egy neurális hálózat minden egyes példával betanítható és tovább javítható, de általában minél nagyobb és komplexebb a hálózat, annál több tanító példára van szükség — a mélytanulás területén gyakran milliók vagy milliárdok mennyiségű adat szükséges a jó teljesítményhez.
Alapfogalmak: rétegek, neuronok és súlyok
Egy tipikus mesterséges neurális hálózat rétegekből áll: bemeneti réteg, egy vagy több rejtett réteg és kimeneti réteg. Minden réteg neuronjai lineáris kombinációt számítanak ki a bemenetekből (súlyokkal és eltolásokkal), majd egy aktivációs függvényt alkalmaznak, amely nemlinearitást visz be, és lehetővé teszi a hálózat számára, hogy összetett mintázatokat tanuljon.
- Neuron: egyszerű számítási egység, amely bemenetek és súlyok alapján kimenetet ad.
- Súlyok és biasok: a hálózat tanulható paraméterei, amelyek a bemenetekhez rendelt fontosságot szabályozzák.
- Aktivációs függvények: például ReLU, sigmoid, tanh — ezek adják meg a nemlinearitást és befolyásolják a tanulás dinamikáját.
Hogyan történik a tanítás?
A tanítás (tréning) során a hálózat paramétereit úgy módosítjuk, hogy a kimenet minél jobban megfeleljen a várt célértékeknek. A leggyakoribb módszer a felügyelt tanulás, ahol ismert bemenet–kimenet párokat használunk. A tanítás fő lépései:
- Előre terjesztés (forward pass): a bemenet áthalad a hálózaton, és megjósoljuk a kimenetet.
- Veszteségszámítás: megmérjük a jóslat hibáját egy veszteségfüggvénnyel (pl. MSE, keresztentrópia).
- Visszaterjesztés (backpropagation): kiszámítjuk a hibára vonatkozó gradiens értékeket a súlyok szerint.
- Optimalizálás: egy algoritmus (például gradient descent, Adam) segítségével frissítjük a súlyokat, hogy csökkentsük a veszteséget.
Tanulási módok
- Felügyelt tanulás: címkézett adatokkal (pl. képek és hozzájuk tartozó osztálycímkék).
- Nem felügyelt tanulás: nincsenek címkék; a hálózat mintázatokat, csoportosításokat vagy reprezentációkat tanul (pl. klaszterezés, autoencoder).
- Megerősítéses tanulás: az ügynök interakcióból és jutalmakból tanul döntéseket hozni (például robotok vagy játékok esetén).
Típusok és architektúrák
Különböző architektúrák különböző feladatokra alkalmasak:
- Feedforward hálózatok: az információ egyirányúan halad előre; egyszerűbb osztályozási problémákra használják.
- Konvolúciós neurális hálózatok (CNN): elsősorban képfeldolgozásra és térbeli mintázatok felismerésére alkalmasak.
- Rekurzív és visszacsatolt hálózatok (RNN, LSTM, GRU): sorozatokkal, időfüggő adatokkal dolgoznak (például beszéd, szöveg).
- Transformer-alapú modellek: ma a természetes nyelvfeldolgozásban (NLP) és más területeken állnak az élvonalban; figyelem (attention) mechanizmuson alapulnak.
Alkalmazások
A neurális hálózatok rendkívül sokoldalúak. Néhány tipikus alkalmazás:
- Számítógépes látás: képosztályozás, objektumdetektálás, képszegmentálás.
- Természetes nyelvfeldolgozás: gépi fordítás, szövegértés, kérdés-válasz rendszerek.
- Beszédfelismerés és beszédszintézis.
- Ajánlórendszerek: személyre szabott tartalom és termékajánlás.
- Egészségügyi diagnosztika: orvosi képek elemzése, betegségkockázat előrejelzése.
- Önvezető járművek, robotika és vezérlési rendszerek.
Előnyök és korlátok
Előnyök:
- Képesek bonyolult, nemlineáris mintázatok felismerésére.
- Rugalmasak — hasonló alapelvekkel sok különböző feladatra alkalmazhatók.
Korlátok és kihívások:
- Nagy mennyiségű tanító adat és számítási erőforrás gyakran szükséges.
- Hajlamosak túlilleszkedni (overfitting), ha nincs elegendő adat vagy megfelelő regulárizáció.
- Gyengén értelmezhetőek: a belső működésük (miért hoznak egy adott döntést) gyakran nem transzparens.
- Adatminőség, torzítások és etikai kérdések komoly hatással lehetnek a rendszerekre.
Gyakorlati szempontok
Amikor neurális hálózatot tervezünk vagy alkalmazunk, érdemes figyelembe venni:
- Adatelőkészítés: normalizálás, hiányzó értékek kezelése, címkék minősége.
- Modellválasztás: egyszerűbb probléma = egyszerűbb modell; túlkomplikálás felesleges költségeket jelent.
- Regularizációs technikák: dropout, L1/L2 büntetés, adataugmentáció a túlilleszkedés csökkentésére.
- Hyperparaméter-keresés: tanulási ráta, rétegszám, neuronszámok, batch méret stb.
- Értékelés: külön train/validation/test felosztás, metrikák (pontosság, precision/recall, F1, ROC-AUC).
Összefoglalás
A mesterséges neurális hálózatok hatékony eszközök összetett mintázatok felismerésére és döntések támogatására sokféle területen. Ugyanakkor megfelelő adat, számítási erőforrás és gondos tervezés szükséges ahhoz, hogy megbízható, igazságos és jól teljesítő megoldásokat kapjunk. A neurális hálózatok a gépi tanulás és a mélytanulás fontos alapelemei, és folyamatosan fejlődnek mind az elméleti hátterük, mind gyakorlati alkalmazásaik terén.
Áttekintés
A neurális hálózatra kétféleképpen gondolhatunk. Az első olyan, mint az emberi agy. A második, mint egy matematikai egyenlet.
Egy hálózat egy bemenettel kezdődik, hasonlóan egy érzékszervhez. Az információ ezután neuronrétegeken keresztül áramlik, ahol minden egyes neuron sok más neuronhoz kapcsolódik. Ha egy adott neuron elég ingerületet kap, akkor az axonján keresztül üzenetet küld bármely más neuronhoz, amelyhez kapcsolódik. Hasonlóképpen, egy mesterséges neurális hálózatnak van egy bemeneti adatrétege, egy vagy több rejtett osztályozó réteg és egy kimeneti réteg. Az egyes rejtett rétegek minden egyes csomópontja a következő réteg egy csomópontjához kapcsolódik. Amikor egy csomópont információt kap, annak egy részét továbbküldi azoknak a csomópontoknak, amelyekhez kapcsolódik. A mennyiséget egy matematikai függvény határozza meg, amelyet aktiválási függvénynek nevezünk, például sigmoid vagy tanh.
Ha úgy gondolunk egy neurális hálózatra, mint egy matematikai egyenletre, akkor a neurális hálózat egyszerűen egy bemenetre alkalmazandó matematikai műveletek listája. Az egyes műveletek bemenete és kimenete egy tenzor (pontosabban egy vektor vagy mátrix). Minden rétegpár a súlyok listájával van összekötve. Minden rétegben több tenzor van tárolva. Egy rétegben lévő egyedi tenzort csomópontnak nevezzük. Minden egyes csomópont a következő réteg néhány vagy összes csomópontjához súlyokkal kapcsolódik. Minden csomópont rendelkezik egy értékek listájával is, amelyet előítéleteknek nevezünk. Az egyes rétegek értéke tehát az aktuális réteg értékeinek (X-nek nevezett) aktiválási függvényéből és a súlyok szorzatából adódik.
A k t i v a t i ó n ( W ( e i g h t s ) ∗ X + b ( i a s ) ) {\displaystyle Activation(W(eights)*X+b(ias))} }
A hálózathoz költségfüggvényt határozunk meg. A veszteségfüggvény azt próbálja megbecsülni, hogy a neurális hálózat mennyire jól teljesíti a kijelölt feladatot. Végül egy optimalizálási technikát alkalmazunk a költségfüggvény kimenetének minimalizálására a hálózat súlyainak és torzításainak megváltoztatásával. Ezt a folyamatot nevezzük képzésnek. A képzés kis lépésekben történik. Több ezer lépés után a hálózat jellemzően már elég jól elvégzi a kijelölt feladatát.
Példa
Vegyünk egy olyan programot, amely ellenőrzi, hogy egy személy él-e. Két dolgot ellenőriz: a pulzust és a légzést.Ha a személynek van pulzusa vagy lélegzik, akkor a program azt adja ki, hogy "él", ellenkező esetben azt, hogy "halott". Egy olyan programban, amely nem tanul az idő múlásával, ezt a következőképpen írnánk le:
Egy nagyon egyszerű, egyetlen neuronból álló neurális hálózat, amely ugyanazt a problémát oldja meg, így néz ki:
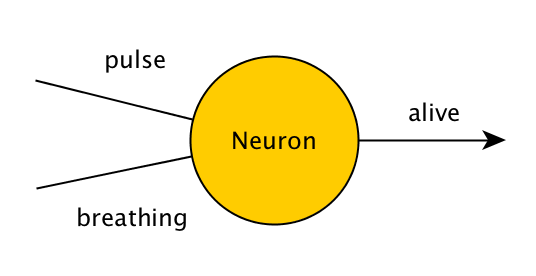
A pulzus, a légzés és az élet értéke 0 vagy 1 lesz, ami a hamis és az igaz értéket jelenti. Ha tehát ez a neuron a (0,1), (1,0) vagy (1,1) értékeket kapja, akkor 1-et kell adnia, ha pedig (0,0) értéket kap, akkor 0-t. A neuron ezt egy egyszerű matematikai művelet alkalmazásával éri el: összeadja a kapott értékeket, majd hozzáadja a saját rejtett értékét, amelyet "torzításnak" nevezünk. Kezdetben ez a rejtett érték véletlenszerű, és idővel módosítjuk, ha a neuron nem a kívánt kimenetet adja.
Ha olyan értékeket adunk össze, mint (1,1), akkor 1-nél nagyobb számokat kaphatunk, de mi azt akarjuk, hogy a kimenetünk 0 és 1 között legyen! Ennek megoldására alkalmazhatunk egy olyan függvényt, amely a tényleges kimenetünket 0-ra vagy 1-re korlátozza, még akkor is, ha a neuron matematikai eredménye nem a tartományon belül volt. Bonyolultabb neurális hálózatokban egy függvényt (például szigmoidot) alkalmazunk a neuronra, hogy annak értéke 0 vagy 1 között legyen (például 0,66), majd ezt az értéket továbbadjuk a következő neuronra egészen addig, amíg szükségünk nem lesz a kimenetünkre.
Tanulási módszerek
Egy neurális hálózat háromféleképpen tanulhat: felügyelt tanulás, felügyelet nélküli tanulás és megerősítéses tanulás. Ezek a módszerek mind egy költségfüggvény minimalizálásával vagy maximalizálásával működnek, de mindegyik jobb bizonyos feladatokban.
Nemrégiben az Egyesült Királyságban található Hertfordshire-i Egyetem kutatócsoportja megerősített tanulást alkalmazott arra, hogy az iCub humanoid robot megtanuljon egyszerű szavakat kimondani gügyögéssel.
Kérdések és válaszok
K: Mi az a neurális hálózat?
V: A neurális hálózat (más néven ANN vagy mesterséges neurális hálózat) egyfajta számítógépes szoftver, amelyet a biológiai neuronok ihlettek. Olyan sejtekből áll, amelyek együtt dolgoznak a kívánt eredmény elérése érdekében, bár minden egyes sejt csak a probléma egy kis részének megoldásáért felelős.
K: Hogyan hasonlítható egy neurális hálózat a biológiai agyakhoz?
V: A biológiai agyak képesek nehéz problémák megoldására, de minden egyes neuron csak a probléma egy nagyon kis részének megoldásáért felelős. Hasonlóképpen, egy neurális hálózat is sejtekből áll, amelyek együtt dolgoznak a kívánt eredmény elérése érdekében, bár minden egyes sejt csak a probléma egy kis részének megoldásáért felelős.
K: Milyen típusú program képes mesterségesen intelligens programokat létrehozni?
V: A neurális hálózatok a gépi tanulás egyik példája, ahol a program képes változni, ahogy megtanulja megoldani a problémát.
K: Hogyan lehet edzeni és minden egyes példával javítani a mélytanulás alkalmazásához?
V: Egy neurális hálózatot minden egyes példával lehet képezni és javítani, de minél nagyobb a neurális hálózat, annál több példára van szüksége ahhoz, hogy jól teljesítsen - a mélytanulás esetében gyakran több millió vagy milliárd példára van szükség.
K: Mire van szükség ahhoz, hogy a mélytanulás sikeres legyen?
V: Ahhoz, hogy a mélytanulás sikeres legyen, több millió vagy több milliárd példára van szükség, attól függően, hogy mekkora a neurális hálózat.
K: Hogyan kapcsolódik a gépi tanulás a mesterségesen intelligens programok létrehozásához?
V: A gépi tanulás azért kapcsolódik a mesterségesen intelligens programok létrehozásához, mert lehetővé teszi, hogy a programok változzanak, ahogy megtanulják, hogyan oldjanak meg problémákat.
Keres
