Megerősítéses tanulás (RL): definíció, alapelvek és példák

Megerősítéses tanulás (RL): világos definíció, alapelvek és gyakorlati példák — áttekintés az ügynökök, jutalmazás, és a felfedezés vs. kihasználás működéséről.

A megerősítéses tanulás mögött álló biológia az Operáns kondicionálás és a Jutalmazás című oldalakon található.

A megerősítéses tanulás (RL) azt jelenti, hogy egy szoftverügynököt megtanítunk arra, hogyan viselkedjen egy környezetben azáltal, hogy megmondjuk neki, milyen jól csinálja. Ez a gépi tanulás egy olyan területe, amelyet a behaviorista pszichológia inspirált.

Az erősítéses tanulás különbözik a felügyelt tanulástól, mivel a helyes bemenetek és kimenetek soha nem jelennek meg. Emellett a megerősítéses tanulás általában menet közben tanul (online tanulás), ellentétben a felügyelt tanulással. Ez azt jelenti, hogy az ágensnek választania kell a felfedezés és aközött, hogy ragaszkodik-e ahhoz, amit a legjobban ismer.

Alapfogalmak

A megerősítéses tanulás központi elemei röviden:

• Ágens (agent): a döntéshozó entitás, amely cselekvéseket hajt végre.
• Környezet (environment): minden, ami az ágenst körülveszi és amelybe az ágens hatással van.
• Állapot (state): a környezet és az ágens pillanatnyi leírása, amely alapján döntést hoz az ágens.
• Cselekvés (action): azok a lehetséges lépések, amelyeket az ágens megtehet.
• Jutalom (reward): visszajelzés a környezettől arról, hogy egy adott cselekvés mennyire volt előnyös (gyakran skalár érték).
• Politika (policy): az ágens stratégiája: hogyan választja a cselekvéseit adott állapotban (determinista vagy valószínűségi).
• Értékfüggvény (value function): megmondja, hogy adott állapotból vagy állapot–cselekvés párosból várhatóan mekkora összegű jutalom származik a jövőben.
• Modell (model): a környezet belső reprezentációja, amely előre jelzi az állapotátmeneteket és jutalmakat (nem minden RL-módszer használ modellt).

Formális keret: Markov-döntési folyamat (MDP)

A legtöbb RL-probléma leírható Markov-döntési folyamattal (MDP). Egy MDP meghatároz egy állapottér, cselekvéstér, átmeneti valószínűségeket és jutalomfüggvényt, valamint gyakran egy diszkonttényezőt (γ), amely a közeli jutalmakat értékesebbé teszi, mint a távolabbiakat. Cél az összesített (diszkontált) jutalom maximalizálása.

Főbb kihívások és elvek

• Felfedezés vs. kiaknázás (exploration-exploitation): az ágensnek egyensúlyt kell találnia az új viselkedések kipróbálása és a már jól bevált viselkedés használata között. Gyakori stratégiák: epsilon-greedy, softmax, UCB.
• Időbeli jóváírás (temporal credit assignment): hogyan tudjuk megítélni, mely korábbi cselekvés(ek) hozták az időben később érkező jutalmat.
• Ritka/gyér jutalmak: sok valós feladatban a jutalom ritkán érkezik, ami megnehezíti a tanulást; ilyenkor segíthet a jutalmazás formázása, belső motiváció vagy imitációs tanulás.
• Mintahatékonyság: mennyi interakció szükséges a jó politikához — model-based módszerek általában hatékonyabbak ebből a szempontból, de bonyolultabbak.
• Funkcióközelítés és stabilitás: mély hálók alkalmazásakor (mély megerősítéses tanulás) instabilitás és divergencia léphet fel; ehhez technikák: replay buffer, target network, normalizáció.

Gyakori algoritmusok és megközelítések

• Model-free módszerek: a környezet modellje nélkül tanulnak. Példák: Q-learning, SARSA, Temporal-Difference (TD) tanulás.
• Model-based módszerek: a környezet modelljét építik meg és azt használják tervezéshez (pl. Dyna, Monte Carlo Tree Search kombinálva modellel).
• Mély RL: neurális hálókat alkalmaznak a politikák és értékfüggvények közelítésére — híres példák: DQN (Deep Q-Network), Deep Deterministic Policy Gradient (DDPG), Proximal Policy Optimization (PPO).
• Policy gradient és actor-critic módszerek: közvetlenül optimalizálják a politikát (REINFORCE, A2C/A3C, PPO, SAC), gyakran actor-critic felépítésben (actor: politika, critic: értékfüggvény).

Alkalmazási területek és példák

• Játékok: Atari-játékok, sakk, go (AlphaGo) — a megerősítéses tanulás vezető sikertörténetei közé tartoznak.
• Robotika: mozgásvezérlés, manipuláció, autonóm navigáció, ahol a valós idejű döntéshozatal és a tanulás kritikus.
• Irányítás és optimalizáció: ipari folyamatok, energiahálózatok, forgalomirányítás.
• Ajánlórendszerek és személyre szabás: hosszú távú felhasználói elégedettség maximalizálása.
• Pénzügyi modellezés és kereskedés: stratégiák tanulása piaci visszajelzések alapján.

Gyakorlati tippek

• Ha ritka jutalmakkal dolgozol, gondolj jutalmazás formázásra, belső jutalmakra (curiosity) vagy utólagos cél-súgásra (hindsight experience replay).
• Használj replay buffert és target hálókat, ha mély hálókkal tanulsz, hogy növeld a stabilitást.
• Figyelj a diszkontfaktor (γ) megválasztására: alacsony γ rövidebb távú célokat preferál, magas γ hosszú távú jutalmakat értékel.
• Teszteld a felfedezési stratégiákat: egyszerű epsilon-greedy sok feladatra működik, de komplexebb problémáknál érdemes adaptív vagy információs alapú megoldásokat alkalmazni.

Összefoglalás

A megerősítéses tanulás egy erőteljes keret döntéshozó rendszerek tanítására, amely a jutalom alapú visszajelzésre épít. Számos elméleti és gyakorlati kihívása van (felfedezés, mintahatékonyság, stabilitás), de a modern algoritmusok és a számítási kapacitás növekedése révén ma már sok területen képes megoldani korábban nehezen kezelhető feladatokat. Az elméleti alapok (pl. operáns kondicionálás) és a gyakorlati technikák is egymást kiegészítve vezettek a terület gyors fejlődéséhez.

Bevezetés

A megerősítéses tanulási rendszer egy szabályzatból ( π {\displaystyle \pi } ), egy jutalomfüggvényből ( R {\displaystyle R} ), egy értékfüggvényből ( v {\displaystyle v} ) és egy választható környezeti modellből áll.

A szabályzat megmondja az ügynöknek, hogy mit kell tennie egy adott helyzetben. Ez lehet egy egyszerű szabálytáblázat, vagy a helyes cselekvés bonyolult keresése. A házirendek lehetnek sztochasztikusak is, ami azt jelenti, hogy a szabályok helyett a házirend valószínűségeket rendel az egyes cselekvésekhez. A házirend önmagában ráveheti az ágenst, hogy tegyen dolgokat, de önmagától nem képes tanulni.

A jutalomfüggvény határozza meg az ágens célját. Befogad egy állapotot (vagy egy állapotot és az abban az állapotban végrehajtott cselekvést), és visszaad egy jutalomnak nevezett számot, amely megmondja az ágensnek, hogy milyen jó az adott állapotban lenni. Az ágens feladata, hogy hosszú távon a lehető legnagyobb jutalmat kapja. Ha egy cselekvés alacsony jutalmat eredményez, akkor az ágens a jövőben valószínűleg egy jobb cselekvést fog végrehajtani. A biológia a jutalomjelzéseket, például az örömöt vagy a fájdalmat használja arra, hogy az élőlények életben maradjanak és szaporodni tudjanak. A jutalomjelzések lehetnek sztochasztikusak is, mint egy kaszinó nyerőgép, ahol néha fizetnek, néha pedig nem.

Egy értékfüggvény megmondja az ágensnek, hogy az s {\displaystyle s} állapotból kiindulva mennyi jutalmat kap egy π {\displaystyle \pi }  politikát követve. Azt fejezi ki, hogy mennyire kívánatos egy adott állapotban lenni. Mivel az értékfüggvényt nem adjuk meg közvetlenül az ágensnek, az eddig kapott jutalom alapján kell kitalálnia egy jó becslést vagy becslést. Az értékfüggvény becslése a legtöbb megerősített tanulási algoritmus legfontosabb része.

A modell az ágens mentális másolata a környezetről. Ezt használják a jövőbeli cselekvések megtervezésére.

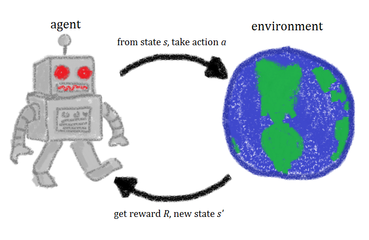
Ennek ismeretében beszélhetünk a megerősítéses tanulási epizód fő hurkáról. Az ágens diszkrét időlépésekben lép kölcsönhatásba a környezettel. Gondoljunk erre úgy, mint egy óra "ketyegésére". A diszkrét időnél a dolgok csak a "ketyegések" és a "tikkek" alatt történnek, a kettő között nem. Minden egyes t = 0 , 1 , 2 , 3 , ... időpontban. {\displaystyle t=0,1,2,3,... } az ágens megfigyeli a környezet S t {\displaystyle S_{t}} állapotát, és kiválaszt egy A t {\displaystyle A_{t}} akciót egy π {\displaystyle \pi } politika alapján. . A következő időlépésben az ágens kap egy R t + 1 {\displaystyle R_{t+1}} jutalomjelzést és egy új megfigyelést S t + 1 {\displaystyle S_{t+1}} . A v ( S t ) {\displaystyle v(S_{t})} értékfüggvényt a jutalom felhasználásával frissítjük. Ez addig folytatódik, amíg el nem érjük az S T {\displaystyle S_{T}} végállapotot.

Keresés betűvel