Lagrange-pont
A Lagrange-pontok a nagy testek közelében lévő stabil pozíciók. Ezekre akkor van példa, amikor két nagy test kering. Ilyen például a Föld és a Nap, illetve a Hold és a Föld pályája.
A pontok öt olyan hely, ahol egy kis tárgy (például egy mesterséges műhold) keringhet. Ezekben a pontokban a két nagy test gravitációs erői és a mozgásból eredő erők mind egyensúlyban vannak. Tehát ezeken a helyeken egy kis tárgy többé-kevésbé stabilan tartja magát. Porfelhők, aszteroidák és mesterséges műholdak találhatók ezekben a pontokban.
Ezt a hatást Joseph-Louis Lagrange matematikusról nevezték el, aki 1772-ben (jóval azelőtt, hogy műholdakat állítottunk volna pályára) írt erről egy tanulmányt.
Az öt helyet L1, L2, L3, L4 és L5-nek hívják. Az első hármat (L1, L2, L3) metastabilnak nevezik, mert ha egy műhold egy kicsit is eltolódik a helyéről, akkor el fog esni attól a ponttól, és nem fog visszatérni üzemanyag felhasználása nélkül. Az L4 és L5 stabilnak tekinthető - ha egy műhold egy kicsit is kimozdul a helyéről, a gravitációs és centripetális erők visszahúzzák a helyére, és a Lagrange-pont körül oszcillál.
A NASA műholdakat helyezett a Nap-Föld rendszer két Lagrange-pontjába. Az L1 pontot (a Föld és a Nap között) a Napot figyelő műholdak számára használják, hogy napkitöréseket keressenek. Az L2 pontot (a Földön túl) az űrteleszkópok számára használják. A James Webb űrteleszkóp is ide fog kerülni, amikor elindítják. Ez egymillió mérföldre (1,6 millió kilométerre) van a Földtől.
Mivel az L4 és L5 stabil, vonzanak porfelhőket és legalább egy aszteroidát (a Föld-Nap rendszer esetében - a nagyobb bolygóknak több aszteroida van az L4 és L5 pontjaikon). Ezeket az aszteroidákat trójai aszteroidáknak nevezik.
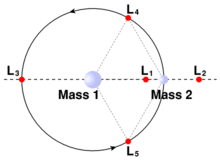
Lagrange-pontok, 2 objektum esetén
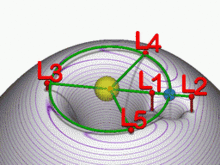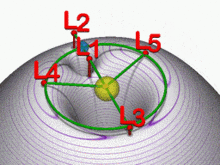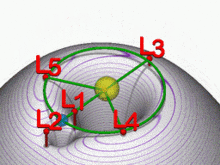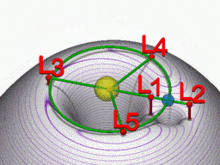
Lagrangian pontok gravitációs kutakkal
Kérdések és válaszok
K: Mik a Lagrange-pontok?
V: A Lagrange-pontok a nagy testek közelében lévő stabil pontok. Amikor két nagy test kering egymás körül, vannak olyan helyek, ahol egy harmadik test meg tud állapodni, lehetővé téve a két nagy test gravitációs és kinetikus erőinek kiegyenlítődését, lehetővé téve a kis test számára, hogy többé-kevésbé stabil maradjon.
K: Ki fedezte fel a Lagrange-pontot?
V: Ez a jelenség Joseph-Louis Lagrange matematikusról kapta a nevét, aki 1772-ben (jóval a műholdak pályára állítása előtt) írt róla egy cikket.
K: Hány Lagrange-pont van?
V: Öt pont van, az L1, L2, L3, L4 és L5.
K: Minden Lagrange-pont stabil?
V: Az első hármat (L1, L2, L3) metastabilnak nevezik, mert ha a műhold kissé eltolódik a helyzetéből, akkor el fog esni attól a ponttól, és nem tér vissza üzemanyag felhasználása nélkül. Ezzel szemben az L4 és L5 stabilnak tekinthető - ha a műhold kissé elmozdul a helyéről, a gravitáció és a centrifugális erő visszahúzza a helyére.
K: Milyen pályát használnak a műholdak ezeken a pozíciókban?
V: Ezeken a helyeken a műholdak a Nap megfigyelésére használhatják a halo pályákat, hogy napkitöréseket keressenek, vagy olyan űrteleszkópok számára, mint a 2021. december 25-én induló James Webb űrteleszkóp, amely mintegy 1,5 millió kilométerre lesz a Földtől.
K. Milyen tárgyak vannak természetes módon jelen ezeken a helyeken?
V: Mivel az L4 és az L5 stabil, vonzották a porfelhőket és a trójai aszteroidákat, amelyek gyakrabban népesítik be a nagyobb bolygókat, mint a kisebb bolygókat, mint például a Föld-Nap rendszer, amely kevés aszteroidát vonzott.
