Impedancia
Az elektromos impedancia az áramkör ellenállásának mértéke az áram vagy feszültség változásával szemben.
Az impedanciát két fő módon lehet leírni: (lásd a 2. ábrát, "komplex impedancia sík")
- az "R" ellenállással (valós rész) és az "X" reaktanciával (képzetes rész), például Z = 1 + 1 j {\displaystyle Z=1+1j}
- egy nagyságrenddel és egy fázissal (a méret | Z | {\displaystyle \left\vert Z\right\vert }
és a szög ∠ θ θ \displaystyle \angle \theta } 
), például Z = 1.4 ∠ 45 ∘ {\displaystyle Z=1.4\angle 45^{\circ }} 
(1,4 ohm 45 fokban)
Az impedancia és az ellenállás nagyon hasonló:
Az ellenállás esetében az ellenállás ellenáll minden rajta áthaladó áramnak. Minél nagyobb az ellenállás, annál nagyobb feszültségre van szükség egy adott áram eléréséhez. A képlet a következő:
V = R ∗ I {\displaystyle V=R*I}
, ahol V a feszültség, R az ellenállás és I az áram.
Az impedancia esetében az induktor az áram, a kondenzátor pedig a feszültség változásának áll ellen.
Az ellenállás és az impedancia közötti legfontosabb különbség a "változás" szó, a változás mértéke befolyásolja az impedanciát. Általában a "változást" frekvenciaként fejezik ki, vagyis az áram vagy a feszültség másodpercenkénti irányváltásainak számaként. A képletek a következők:
Az induktorhoz: Z = j 2 π f L {\displaystyle Z=j2\pi fL\,} 
A kondenzátorhoz: Z = 1 j 2 π f C {\displaystyle Z={\frac {1}{j2\pi fC}}} 
Ahol Z az impedancia szimbóluma, j a képzeletbeli szám - 1 {\displaystyle {\sqrt {-1}}} 
, π {\displaystyle \pi }
a pi állandó, f a frekvencia, L az induktivitás és C a kapacitás. Az ellenállás és az impedancia mértékegysége ugyanaz, az Ω {\displaystyle \Omega} jelű ohm. 
(nagy ómega).
Amint a fenti képletekből kitűnik, az impedancia a frekvenciától függően változik, például nulla Hertz vagy egyenáram esetén az induktor impedanciája nulla, ami rövidzárlatnak felel meg, a kondenzátor impedanciája pedig végtelen, ami nyitott áramkörnek felel meg. A legtöbb jel sok különböző frekvenciájú szinuszhullám összege (további részletekért lásd a Fourier-transzformációt), és mindegyikük különböző impedanciát tapasztal.
Az ellenálláshoz hasonlóan minél nagyobb az impedancia, annál nagyobb feszültségre van szükség egy adott áram eléréséhez. A képlet a következő:
V = Z ∗ I {\displaystyle V=Z*I}
, ahol V a feszültség, Z az impedancia, I pedig az áram.
Fizikai szinten sok mindent leegyszerűsítve:
- az ellenállást az elektronoknak az ellenállásban lévő atomokkal való ütközése okozza.
- a kondenzátor impedanciáját az elektromos mező létrejötte okozza.
- az impedanciát egy induktorban a mágneses mező létrehozása okozza.
Az egyik fontos különbség az ellenállás és az impedancia között az, hogy az ellenállás energiát vezet le, felmelegszik, de az induktor és a kondenzátor tárolja az energiát, és vissza tudja adni az energiát a forrásnak, amikor az lemerül.
Ha a forrás, a kábel és a terhelés impedanciája nem egyenlő, akkor a jel egy része visszaverődik a forrásra, ami energiát pazarol és interferenciát okoz. A visszaverődés aránya a következőkkel számítható ki:
Γ = Z L - Z S Z L + Z S {\displaystyle \Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}}
ahol Γ {\displaystyle \Gamma}} 
(nagy gamma) a reflexiós tényező, Z S {\displaystyle Z_{S}}
a forrás impedanciája, Z L {\displaystyle Z_{L}}
a terhelés impedanciája.
Minden olyan közegnek, amelyben hullámok lehetnek, van hullámimpedanciája, még az üres térnek is (a fény elektromágneses hullám, és képes a térben utazni) körülbelül 377 Ω impedanciája van. .
A jel részben visszaverődik, ahol az impedancia megváltozik.
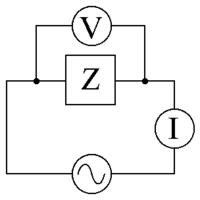
V {\displaystyle \scriptstyle V} feszültséget alkalmazó váltakozó áramú tápegység. 
egy Z {\displaystyle \scriptstyle Z} impedancián keresztül. 
I {\displaystyle \scriptstyle I}
áramot vezet.
A komplex impedancia sík grafikus ábrázolása
Fázis
Egy ellenálláson keresztül mind a feszültség, mind az áram egyszerre megy fel és le, azt mondják, hogy fázisban vannak, de egy impedanciával ez másképp van, a feszültség 1/4 hullámhosszal eltolódik az áram mögött egy kondenzátorban, és előre egy induktorban.
Az 1/4 hullámhosszat általában a "j" képzeletbeli számmal ábrázolják, ami szintén 90 fokos eltolódásnak felel meg.
A "j" képzeletbeli szám használata sokkal egyszerűbbé teszi a matematikát, lehetővé teszi a teljes impedancia kiszámítását ugyanúgy, mint az ellenállások esetében, például egy ellenállás plusz egy impedancia sorozatban R+Z, párhuzamosan pedig (R*Z)/(R+Z).
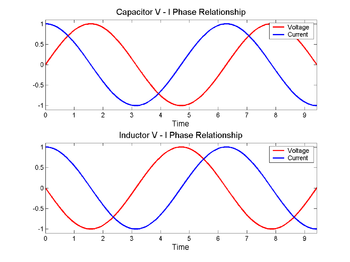
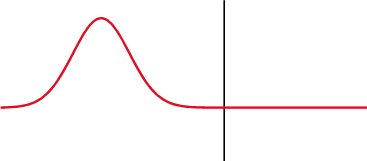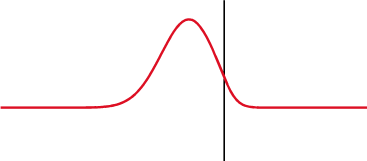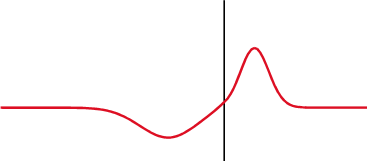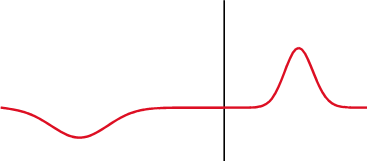
Egy kondenzátoron (fent) a feszültség (piros) az áram (kék) után változik, egy induktoron (lent) pedig előtte. A feszültség és az áram közötti fáziskülönbség 1/4 hullámhossz.
Kérdések és válaszok
K: Mi az elektromos impedancia?
V: Az elektromos impedancia az az ellenállás mértéke, amelyet egy áramkör az áram vagy a feszültség változásával szemben tanúsít.
K: Hogyan írható le az elektromos impedancia?
V: Az elektromos impedancia leírható az "R" ellenállással (valós rész) és az "X" reaktanciával (képzetes rész), valamint nagysággal, fázissal, mérettel és szöggel.
K: Mi a különbség az ellenállás és az impedancia között?
V: Az ellenállás és az impedancia közötti legfontosabb különbség a "változás" szó; más szóval a változás mértéke befolyásolja az impedanciát. Az ellenállás ellenáll minden rajta áthaladó áramnak, míg az induktor az áram változásának, a kondenzátor pedig a feszültség változásának.
K: Milyen képletek kapcsolódnak az ellenálláshoz és az impedanciához?
V: Ellenállás esetén V=R*I, ahol V a feszültség, R az ellenállás és I az áram; induktorok esetén Z=j2πfL; kondenzátorok esetén Z=1/j2πfC; ahol Z az impedanciát, j a képzeletbeli számot -1 , π a konstans pi-t, f a frekvenciát, L az induktivitást, C a kapacitást jelenti.
K: Milyen fizikai magyarázatot adhatunk az ellenállás és az impedancia közötti összefüggésre?
V: Az ellenállást az ellenállásokban lévő atomokkal ütköző elektronok okozzák, míg az induktor impedanciája elektromos mező létrehozásából, a kondenzátoré pedig mágneses mező létrehozásából származik. Ezenkívül az ellenállások energiát vezetnek el, míg az induktorok és a kondenzátorok energiát tárolnak, amelyet aztán vissza lehet juttatni a forráshoz, amikor az lecsökken.
K: Hogyan kell kiszámítani a reflexiós együtthatót?
V: A reflexiós együttható a Γ=(ZL-ZS)/(ZL+ZS) segítségével számítható ki, ahol Γ (nagy gamma) a reflexiós együtthatót jelenti; ZS a forrás impedanciáját jelenti; ZL a terhelés impedanciáját jelenti.
