AlegsaOnline.com

Gravitációs gyorsulás: definíció, mérték és Földi érték (g = 9,80665 m/s²)

Ismerd meg a gravitációs gyorsulás fogalmát, mértékét és a Föld standard értékét (g = 9,80665 m/s²) — magyarázat, képletek és helytől függő változások érthetően.

Szerző: Leandro Alegsa

12-01-2026

A gravitációs erő hatására egy tárgy által elért gyorsulást nevezzük a gravitáció miatti gyorsulásnak. SI‑egysége m/s². A gravitációs gyorsulás vektor, ami azt jelenti, hogy van nagysága és iránya is: a Föld közelében tipikusan a testre ható erő irányába, a Föld középpontja felé mutat. A Föld felszínén a gravitációs gyorsulást a g betűvel jelöljük; a nemzetközi szabvány szerinti referenciérték (standard gravity) g₀ = 9,80665 m/s² (≈ 32,17405 ft/s²).

Matematikai leírás

Az ideálisizált esetben, egy gömbszimmetrikus test (például tökéletesen gömb alakú bolygó) felszínén a gravitációs gyorsulás nagysága a Newton‑féle formulával adható meg:

g = G·M / r²

G a gravitációs állandó (≈ 6,67430·10⁻¹¹ m³·kg⁻¹·s⁻²),
M a központi tömeggel rendelkező égitest tömege (a Föld tömege ≈ 5,972·10²⁴ kg),
r a távolság a test tömegközéppontjától (felszínen kb. a Föld sugara ≈ 6,371 km).

Fontos megjegyezni, hogy ez a képlet a gravitációs tér részecskére gyakorolt helyi gyorsulását adja meg; a valóságban az effektív gyorsulást a gravitáció és a centrifugális hatás együttese adja.

Miért változik a g a Földön?

A Földön a ténylegesen mért g nem teljesen állandó, több tényező befolyásolja:

Föld sugara és alakja: mivel a Föld nem tökéletes gömb, hanem forgás miatt kissé lapult (geoid/ellipszoid), a sarkoknál közelebb vanunk a tömegközépponthoz, így ott nagyobb a gravitáció (≈ 9,832 m/s²) mint az egyenlítőn (≈ 9,780 m/s²).
Forgásból adódó centrifugális gyorsulás: a Föld forgása csökkenti az effektív szabadesési gyorsulást, a hatás legnagyobb az egyenlítőn, a pókon nulla.
Magasság (távolság a Föld középpontjától): növekvő magasságban a g csökken (például a Nemzetközi Űrállomáson m/s² nagyságrendű kisebb, de az állandó szabadon hullás miatt ott is „súlytalansághoz” hasonló állapot látszik).
Lokális sűrűségkülönbségek: geológiai szerkezetek (hegységek, üregek, ásványkincsek) helyi eltéréseket okoznak, amelyeket geofizikai gravimetriai mérésekkel térképeznek.

Tipikus értékek és egységek

Standard gravity: g₀ = 9,80665 m/s² (CGPM által definiált referenciapont).
Földi tartomány: nagyjából 9,78–9,83 m/s² a szélességi és magassági eltérések miatt.
Más égitestek: Holdon ≈ 1,62 m/s², Marson ≈ 3,71 m/s², Jupiteren sokkal nagyobb értékek fordulnak elő a tömeg és sugár függvényében.
Gal egység: geofizikában gyakran használják a gal-t (1 gal = 1 cm/s²), tehát g₀ ≈ 980,665 gal.

Mérés és gyakorlat

A gravitációs gyorsulást különböző módszerekkel mérik:

Szabadeséses vizsgálatok: pontos időméréssel és távolsággal meghatározható a gyorsulás.
Graviméterek: érzékeny műszerek, amelyek kis lokális változásokat is kimutatnak (geofizikai kutatásokhoz, olaj- és ásványkutatáshoz).
Inerciális navigáció és mérőműszerek: a járművek és hajók rendszerében fontos az aktuális helyi g ismerete.

Gyakori félreértések

A „súly” és a „gravitációs gyorsulás” nem pontosan ugyanaz: a súly (F = m·g) a gravitációs gyorsulás és a test tömegének szorzata; emellett a forgásból vagy más gyorsulásokból származó erők is módosíthatják a mért „súlyt”.
„Nulla g” a világűrben: a Nemzetközi Űrállomáson tapasztalt úgynevezett súlytalanság nem azt jelenti, hogy nincs gravitáció — sokkal inkább azt, hogy az állomás és a benne levő tárgyak ugyanazzal a szabadesési pályával esnek, így relatív gyorsulásuk nulla.

Összefoglalva: a gravitációs gyorsulás (g) a gravitációs erő által keltett lokális gyorsulás, vektormennyiség, melynek szabványos referenciája g₀ = 9,80665 m/s², de a Földön a tényleges érték földrajzi helytől és magasságtól függően változik.

Miért nem esnek gyorsabban a nehezebb tárgyak, mint a könnyebbek?

Isaac Newton kiszámította, hogy az eredő erő egyenlő a tömeg és a gyorsulás szorzatával, vagy szimbólumokkal: F = m a {\displaystyle F=ma} $F=ma$ . Ez átrendezhető úgy, hogy a = F m {\displaystyle a={\frac {F}{m}}}\ } } $a={\frac {F}{m}}\$ . Minél nagyobb a zuhanó tárgy tömege, annál nagyobb a gravitációs vonzóerő, amely a Föld felé húzza. A fenti egyenletben ez F {\displaystyle F} . Az erő azonban annyiszor lesz nagyobb vagy kisebb, ahányszor a tömeg nagyobb vagy kisebb lesz, az arány állandó marad. Minden helyzetben az F m {\displaystyle {\frac {F}{m}}}\ } ${\frac {F}{m}}\$ eltörlődik a 9,8 m/s körüli egyenletes gyorsulásig² . Ez azt jelenti, hogy tömegüktől függetlenül minden szabadon eső tárgy ugyanolyan sebességgel gyorsul.

Vegyük a következő példákat:

a = 49 N 5 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} } $a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}}$

a = 147 N 15 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} } $a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}}$

Felületi gyorsulás

A helytől függően egy tárgy a Föld felszínén 9,76 és 9,83 m/s² (32,0 és 32,3 ft/s² ) közötti gyorsulással esik.

A Föld nem pontosan gömb alakú. Inkább egy "összenyomott" gömbhöz hasonlít, amelynek sugara az egyenlítőnél valamivel nagyobb, mint a pólusoknál. Ennek az a hatása, hogy a gravitációs gyorsulás a pólusoknál kissé megnő (mivel közel vagyunk a Föld középpontjához, és a gravitációs erő a távolságtól függ), az egyenlítőnél pedig kissé csökken. Továbbá a centripetális gyorsulás miatt a gravitáció okozta gyorsulás az egyenlítőnél valamivel kisebb, mint a sarkoknál. A talaj alatti kőzet sűrűségének változása vagy a közelben lévő hegyek jelenléte kissé befolyásolhatja a gravitációs gyorsulást.

Magasság

Egy tárgy gyorsulása a magassággal változik. A gravitációs gyorsulás változása a Föld középpontjától mért távolsággal a fordított négyzetes törvényt követi. Ez azt jelenti, hogy a gravitációs gyorsulás fordítottan arányos a Föld középpontjától mért távolság négyzetével. A távolság megduplázódásával a gravitációs gyorsulás 4-szeresére csökken, a távolság megháromszorozódásával a gravitációs gyorsulás 9-szeresére csökken, és így tovább.

gravitációs gyorsulás ∝ 1 távolság 2 {\displaystyle {\mbox{gravitációs gyorsulás}}\ \propto \ {\frac {1}{{{\mbox{távolság}}^{2}}}}\ }\ } ${\mbox{gravitational acceleration}}\ \propto \ {\frac {1}{{\mbox{distance}}^{2}}}\$

gravitációs gyorsulás × távolság 2 = k {\displaystyle {\mbox{gravitációs gyorsulás}}\ \ \times {{\mbox{távolság}}^{2}}\ ={k}} ${\mbox{gravitational acceleration}}\ \times {{\mbox{distance}}^{2}}\ ={k}$

A Föld felszínén a gravitáció okozta gyorsulás nagyjából 9,8 m/s² (32 ft/s² ). A Föld középpontjától mért átlagos távolság 6 371 km (3 959 mi).

k = 9.8 × 6371 2 {\displaystyle {k}={\mbox{9.8}}}\ \times {{\mbox{6371}}}^{2}}}} ${k}={\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}$

A k {\displaystyle k} állandó használatával kiszámíthatjuk a gravitációs gyorsulást egy bizonyos magasságban.

gravitációs gyorsulás = k távolság 2 {\displaystyle {\mbox{gravitációs gyorsulás}}\ ={\frac {k}{{{\mbox{távolság}}^{2}}}}}}\ } } ${\mbox{gravitational acceleration}}\ ={\frac {k}{{\mbox{distance}}^{2}}}\$

Példa: Keresse meg a gravitáció okozta gyorsulást 1000 km (620 mi) magasságban a Föld felszíne felett.

6371 + 1000 = 7371 {\displaystyle 6371+1000=7371} $6371+1000=7371$

∴ A Föld középpontjától való távolsága 7 371 km (4 580 mi).

gravitációs gyorsulás = 9.8 × 6371 2 7371 2 ≈ 7.3 {\displaystyle {\mbox{gravitációs gyorsulás}}\ ={\frac {\mbox{9.8}}\ \times {{\mbox{6371}}}^{2}}}}{{\mbox{7371}}}^{2}}}}\ \approx 7.3}\ ${\mbox{gravitational acceleration}}\ ={\frac {{\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}}{{\mbox{7371}}^{2}}}\ \approx 7.3$

∴ A gravitáció okozta gyorsulás 1000 km (620 mi) magasságban a Föld felszíne felett 7,3 m/s² (24 ft/s² ).

A gravitációs gyorsulás a Kármán-vonalon, a Föld légköre és a világűr közötti határon, amely 100 km magasságban van, csak mintegy 3%-kal alacsonyabb, mint a tengerszinten.

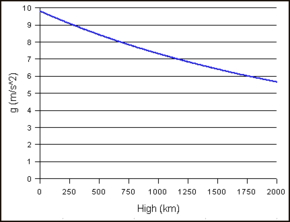
A gravitációs gyorsulás változása a tárgy magasságával

Kérdések és válaszok

K: Mi a gravitáció okozta gyorsulás?

V: A gravitáció miatti gyorsulás az a gyorsulás, amelyet egy tárgy a gravitációs erő hatására kap.

K: Mi a gravitációs gyorsulás SI-egysége?

V: A gravitációs gyorsulás SI-egysége m/s2.

K: A gravitációs gyorsulás skalár vagy vektor?

V: A gravitáció okozta gyorsulás vektor, mert van nagysága és iránya is.

K: Milyen szimbólummal jelölik a Föld felszínén a gravitáció okozta gyorsulást?

V: A Föld felszínén a gravitáció okozta gyorsulást a g jelöli.

K: Mekkora a Föld felszínén a gravitáció okozta gyorsulás standard értéke?

V: A Föld felszínén a gravitációs gyorsulás standard értéke 9,80665 m/s2 (32,1740 ft/s2).

K: Változik-e egy szabadesésben lévő test tényleges gyorsulása a helytől függően?

V: Igen, a szabadesésben lévő test tényleges gyorsulása a hely függvényében változik.

K: Mi a gravitációs gyorsulás definíciója?

V: A gravitáció miatti gyorsulás a gravitációs erő hatására egy tárgy által elért gyorsulás, amelyet a g betűvel jelölünk, és amelynek szabványos értéke a Föld felszínén 9,80665 m/s2 , míg a tényleges gyorsulás a helytől függően változhat.