Matematikai jel (előjel): pozitív, negatív számok és szimbólumok
Ismerd meg a matematikai jeleket: előjelek, pozitív és negatív számok, nulla és gyakori szimbólumok egyszerű magyarázattal és példákkal.
A matematikában a jel szó általában arra a tulajdonságra utal, hogy egy szám vagy érték pozitív vagy negatív. Minden olyan valós szám, amely nem nulla, vagy pozitív, vagy negatív — tehát rendelkezik előjellel. Maga a nulla előjel nélküli (szokás azt mondani, hogy sem pozitív, sem negatív), illetve technikailag egyszerre nemnegatív és nempozitív. Ha egy számot jel nélkül írunk, a megszokott értelmezés szerint pozitívnak tekintjük.
Pozitív és negatív számok, előjelek
A számok előjelét a legegyszerűbben a következő szimbólumok jelölik:
- + : pozitív előjel (például +3), gyakran elhagyjuk és egyszerűen 3-ként írjuk;
- - : negatív előjel (például -5), azt jelzi, hogy a szám 0-nál kisebb;
- ± : két lehetőség (például x = ±2 jelentése x = 2 vagy x = -2), gyakran egyenletek megoldásánál használjuk;
- ∓ : általában együtt szerepel a ±-vel kombinatív jelentésben (pl. ±/∓ párok az összefüggésekben).
Alapműveletek előjellel
- Összeadás és kivonás: a pozitív és negatív számok összeadásakor vagy kivonásakor az előjelek figyelembevételével végezzük el a műveletet (például 3 + (−2) = 1, −3 + (−2) = −5, 3 − 5 = −2).
- Szorzás és osztás: a szabály egyszerű: két azonos előjelű szám szorzata/osztása pozitív, két különböző előjelűé negatív. Példák: (−2)·(−3) = 6, (−4)·3 = −12, (−6)/ (−2) = 3.
- Előjeltől való megszabadulás: két egymás utáni mínusz előjel megszünteti egymást: −(−a) = a.
Jelfüggvény és abszolút érték
Gyakran használjuk a jelfüggvényt (sgn), amely megadja egy szám előjelét:
- sgn(x) = 1, ha x > 0;
- sgn(x) = 0, ha x = 0;
- sgn(x) = −1, ha x < 0.
Az abszolút érték |x| a szám nagyságát (távolságát a nullától) adja előjel nélkül: |−3| = 3, |3| = 3. Kapcsolatban: x = sgn(x)·|x|, ha x ≠ 0.
A jel szó más értelmei a matematikában
A jel kifejezést nem csak a számok előjelére használjuk. Például beszélünk jelekről mint matematikai szimbólumokról (pl. +, −, ×, ÷), illetve a jel szó megjelenik más területeken is, például függvények pozitív és negatív részeinek jelölésében vagy fizikai mennyiségek irányának kifejezésében. Fontos megkülönböztetni a „jel” mint előjel fogalmát a műveleti jelektől (pl. az összeadás jele + mint műveleti szimbólum).
Összefoglalás
- A nem nulla valós számok rendelkeznek előjellel: vagy pozitívak, vagy negatívak.
- A nulla különleges: előjel nélküli, ugyanakkor egyszerre tekinthető nemnegatívnak és nempozitívnak.
- A műveleteknél az előjelek szabályai egyszerűen alkalmazhatók: szorzásnál és osztásnál azonos előjelek pozitív eredményt adnak, különböző előjelek negatívat.
- A jel és a jelzés (szimbólum) fogalma több matematikai kontextusban is előfordul, ezért érdemes pontosan megkülönböztetni a jelentéseket.

A plusz és mínusz szimbólumok a számok előjelét mutatják. A plusz pozitív, a mínusz pedig negatív számot jelent.
Egy szám jele
Egy valós szám akkor pozitív, ha nagyobb, mint nulla, és akkor negatív, ha kisebb, mint nulla. A pozitív vagy negatív tulajdonságot a szám előjelének nevezzük. Magának a nullának nincs előjele.
A számtanban a számok előjelét gyakran úgy jelölik, hogy a szám elé plusz vagy mínusz jelet tesznek. Például a +3 a pozitív 3-at, a -3 pedig a negatív 3-at jelöli. Ha nincs plusz- vagy mínuszjel, akkor a legfőbb módon azt látjuk, hogy a szám pozitív.
Bármely nem nulla szám előjele pozitívra változtatható az abszolút érték függvény segítségével. Például a -3 abszolút értéke és a 3 abszolút értéke is egyenlő 3. Szimbólumokban ezt úgy írnánk, hogy |-3| = 3 és |3| = 3.
A nulla jele
A nulla szám se nem pozitív, se nem negatív, ezért nincs előjele. A számtanban a +0 és a -0 egyaránt ugyanazt a 0 számot jelenti.
A jelek jelentése
Mivel a nulla nem pozitív és nem negatív, az ismeretlen szám előjelére néha az alábbiakat használják:
- Egy szám akkor pozitív, ha nagyobb, mint nulla.
- Egy szám akkor negatív, ha nulla alatt van.
- Egy szám akkor nem negatív, ha nagyobb vagy egyenlő nullánál.
- Egy szám akkor nem pozitív, ha kisebb vagy egyenlő nullával.
Így egy nem negatív szám vagy pozitív vagy nulla, míg egy nem pozitív szám vagy negatív vagy nulla. Például egy valós szám abszolút értéke mindig nem negatív, de nem feltétlenül pozitív.
Néha ugyanezt a definíciót használják olyan függvények esetében is, amelyek valós vagy egész értékeket vesznek fel. Például egy függvényt pozitívnak nevezünk, ha minden értéke pozitív, vagy nemnegatívnak, ha minden értéke nemnegatív.
Egy szög jele
Sok szövegben gyakran előfordul, hogy egy jelet egy szög, különösen egy elhelyezkedő szög vagy egy forgásszög mértékével együtt látunk. Ilyen helyzetben a jel azt mondja meg, hogy a szög az óramutató járásával megegyező vagy ellentétes irányú. Bár különböző konvenciókat lehet használni, a matematikában gyakori, hogy az óramutató járásával ellentétes irányú szögek pozitívnak, az óramutató járásával megegyező irányú szögek pedig negatívnak számítanak.
Három dimenzióban is lehet jelet adni egy forgásszögnek, feltéve, hogy a forgástengelyt eligazítottuk. Konkrétan, egy tengely körüli jobbra fordulás általában pozitívnak, míg egy balra fordulás negatívnak számít.
Egy irány jele
A számtanban és a fizikában gyakori, hogy bizonyos irányokat pozitívnak vagy negatívnak jelölünk. Egy alapvető példával élve, a számegyenest általában úgy rajzolják meg, hogy a pozitív számok jobbra, a negatív számok pedig balra vannak:
![]()
A kartéziánus síkban a jobbra és a felfelé mutató irányokat általában pozitívnak gondoljuk, a jobbra mutató a pozitív x-irány, a felfelé mutató pedig a pozitív y-irány.
Egyéb jelentések
A valós számok jele mellett a matematikában és a természettudományokban a jel szót számos kapcsolódó módon is használják:
- A gráfelméletben az előjeles gráf olyan gráf, amelyben minden él pozitív vagy negatív előjellel van jelölve.
- A fizikában minden elektromos töltésnek van egy jele, pozitív vagy negatív. Az általános szabályok szerint a pozitív töltés a protonéval megegyező előjelű töltés, a negatív töltés pedig az elektronéval megegyező előjelű töltés.
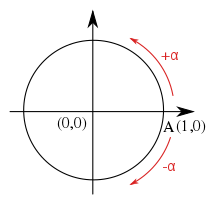
Az x-tengelytől mérve az egységkörön az óramutató járásával ellentétes irányban a szögek pozitívnak, az óramutató járásával ellentétes irányban pedig negatívnak számítanak.
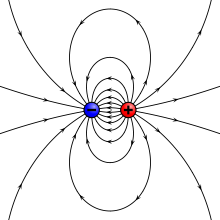
Az elektromos töltés lehet pozitív vagy negatív.
Keres