Valószínűség (valószínűségszámítás): definíció, szabályok és példák
Valószínűség (valószínűségszámítás): világos definíciók, szabályok és lépésről lépésre példák kezdőknek és haladóknak — tanulj könnyen és számolj magabiztosan!
A valószínűségszámítás a alkalmazott matematika egyik ága. A véletlennel kapcsolatos jelenségek modellezésével és elemzésével foglalkozik: olyan helyzetekkel, amikor többféle kimenetel is lehetséges, és ezekhez különböző mértékű „esélyek” vagy valószínűségek rendelhetők.
Például egy érmével történő dobásnál a valószínűségszámítás segítségével megfogalmazhatjuk és igazolhatjuk, hogy ha az érme tisztességes (nincs eltorzulva), akkor nagy számú ismétlés esetén körülbelül az esetek felében az egyik, a másik felében pedig a másik oldal lesz felfelé. Az érme egyik oldalát gyakran fejnek, a másikat írásnak nevezzük.
Egy esemény valószínűsége (P) mindig 0 és 1 közé esik: 0 azt jelenti, hogy az esemény soha nem következik be (lehetetlen), 1 pedig hogy mindig bekövetkezik (biztos).
Alapfogalmak
Mintatér (mintaalap): az összes lehetséges kimenetel halmaza, jelölése gyakran Ω. Például egy szabályos kocka dobásánál Ω = {1,2,3,4,5,6}.
Esemény: a mintatér részhalmaza. Például „páratlan szám dobása” az {1,3,5} esemény.
Osztályos (klasszikus) valószínűség: ha minden kimenetel egyformán valószínű és a mintatér véges, akkor egy esemény valószínűsége a kedvező kimenetelek száma osztva a lehetséges kimenetelek számával. Példa: ha dobunk egy kockát, annak az esélye, hogy az 1-re esik, 1/6, mert 1 kedvező kimenetel van a 6 lehetségesből.
Szabályok és tételek
1) Összegszabály (két eseményre):
- Ha A és B kizárják egymást (egyszerre nem következhetnek be), akkor P(A ∪ B) = P(A) + P(B).
- Általánosan: P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
2) Komplementer szabály: Ha A egy esemény, akkor a nem-A esemény valószínűsége P(A^c) = 1 − P(A). Ezt gyakran használják „legalább egy” típusú eseményeknél: például az esélye, hogy legalább egy hatost dobunk n egymás utáni kockadobásból, 1 − (5/6)^n.
3) Szorzatszabály (egymástól független események): Ha A és B függetlenek (egyik bekövetkezése nem befolyásolja a másikat), akkor P(A ∩ B) = P(A) · P(B). Példa: két kockadobásnál a 3-as majd 5-ös sorrend valószínűsége (1/6)·(1/6) = 1/36 ≈ 0,0277.
Általános szorzatszabály: P(A ∩ B) = P(A) · P(B | A), ahol P(B | A) a B esemény valószínűsége feltéve, hogy A bekövetkezett.
4) Feltételes valószínűség: P(B | A) = P(A ∩ B) / P(A), feltéve hogy P(A) > 0. Ez a szabály alapja a Bayes-tételnek és sok gyakorlati számításnak.
5) Függetlenség: A és B események függetlenek, ha P(A ∩ B) = P(A)P(B). Fontos megjegyezni, hogy függetlenség nem azonos a kizárólagossággal; két kizárt esemény nem lehet független, kivéve ha az egyik valószínűsége 0.
Gyakorlati példák
- Egy szabályos kocka dobásakor P(1) = 1/6, P(páratlan szám) = 3/6 = 1/2.
- Két kocka dobása: a teljes mintatér 36 kimenetelből áll (6×6). A „két hatos” valószínűsége 1/36. A dobott számok összege 7 valószínűsége 6/36 = 1/6, mert a következő párok adják össze 7-et: (1,6),(2,5),(3,4),(4,3),(5,2),(6,1).
- Többszöri dobások: annak valószínűsége, hogy három egymás utáni dobásban először 3-as, majd 5-ös, majd 2-es lesz, (1/6)^3 = 1/216 ≈ 0,00463.
- „Legalább egy hatos” példája n dobásra: P(legalább egy hatos) = 1 − P(nincs hatos) = 1 − (5/6)^n. Például 3 dobásnál ez 1 − (5/6)^3 ≈ 0,4213 (kb. 42,13%).
Bonyolultabb számítások és megközelítések
Néha a valószínűségek kiszámítása nem triviális: például ha sok kockát dobunk egyszerre (például hat kockával), és azt vizsgáljuk, hogy milyen az összeg eloszlása, akkor kombinatorikai számításokra vagy valószínűségi eloszlások konvolúciójára van szükség. Nagyszámú ismétlés esetén gyakran használjuk a központi határeloszlás tételét, amely közelítő módon normál eloszlást ad az összegre.
Megjegyzés a szemléletmódokról: A valószínűség értelmezhető gyakoriságként (hosszú távú arányként) vagy szubjektív mértékként (hiedelem mértékeként). A matematika ugyanakkor mindkét megközelítést kiszolgáló formális szabályrendszert ad.
Összefoglalás
- Valószínűség értéke 0 és 1 között van.
- Ha a mintatér véges és minden kimenetel egyforma, P(A) = kedvező kimenetelek száma / összes kimenetel száma.
- Hasznos szabályok: komplementer, összeadás két eseményre, szorzás (függetlenség esetén), feltételes valószínűség.
- Gyakori feladatok: „legalább egy”, „pontosan k” típusú kérdések, függetlenség vizsgálata, feltételes események elemzése.
Ha szeretnéd, készítek konkrét számításokat, például kiszámolom egy vagy több kockával kapcsolatos valószínűséget lépésről lépésre, vagy bemutatok Bayes-tételre egy ismert példát.
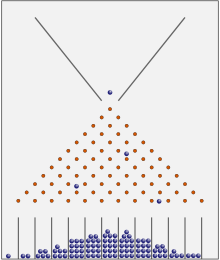
A babgépben vagy a Galton-dobozban a legtöbb golyó a középponthoz közel kerül. Hosszú távon normális eloszlást fognak mutatni.
A valószínűséggel kapcsolatos elképzelések
Olyan emberek, mint Jacob Bernoulli, Pierre-Simon Laplace vagy Christiaan Huygens használták a valószínűség szót, a fent leírtak szerint. Mások gyakoriságokról gondolkodtak; a valószínűség fogalmát általában gyakorisági valószínűségnek nevezik.
Kapcsolódó oldalak
- A matematikai témák listája
- Valószínűségelmélet
Kérdések és válaszok
K: Mi a valószínűség?
V: A valószínűség az alkalmazott matematika egy része, amely olyan dolgok tanulmányozásával foglalkozik, amelyek megtörténhetnek vagy nem történhetnek meg.
K: Hogyan fejezhető ki a valószínűség?
V: A valószínűség kifejezhető egy nulla (lehetetlen) és egy (biztos) közötti számmal.
K: Mi a példa a valószínűség használatára?
V: A valószínűség használatára példa, ha megmutatjuk, hogy ha egy érmét a levegőbe dobunk, és hagyjuk, hogy földet érjen, akkor az esetek felében az egyik oldala felfelé, a másik felében pedig a másik oldala felfelé fog landolni.
K: Hogyan lehet kiszámítani annak a valószínűségét, hogy két kockával dobva egy bizonyos kombinációt kapunk?
V: Ha ki akarod számítani annak a valószínűségét, hogy két kockával dobsz és egy bizonyos kombinációt kapsz, akkor szorozd meg a két valószínűségüket. Ha például tudni szeretnéd, hogy mekkora a valószínűsége annak, hogy 3-as, majd 5-ös dobást kapsz, akkor ez 1/6 x 1/6 = 1/36 lenne.
K: Mire utal az "írás" kifejezés, amikor érmékről beszélünk?
V: Amikor érmékről beszélünk, a "farok" azt az oldalt jelenti, amelyen nincs arc vagy kép.
K: Milyen valószínű, hogy hat kockával dobva tíznél nagyobb számot kapunk? V: Annak a valószínűsége, hogy hat kockával dobva tíznél nagyobb számot kapunk, matematikai és tudományos módszerekkel kiszámítható, de nem nyilvánvaló.
K: Mi történik, ha két valószínűséget összeszorzunk?
V: Amikor két valószínűséget összeszorzol, akkor annak az esélyét számolod ki, hogy mindkét dolog egyszerre fog bekövetkezni.
Keres