Histogram
A hisztogram a statisztika egyik fogalma. Ez egy olyan grafikus megjelenítés, amely az érintett minták eloszlásáról árulkodik. Általában egy sok kategóriát tartalmazó táblázatból készített képet ábrázolnak. A táblázat megmondja, hogy az egyes kategóriákban hány minta található.
A hisztogram szó a görög histos és gramma szavakból származik. A hisztosz hálót vagy árbocot jelent. A gramma rajzot, feljegyzést vagy írást jelent. A hisztogram tehát etimológiai értelemben valaminek a szövedékéről készült rajz.
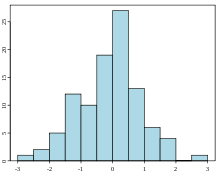
Példa 100 normális eloszlású véletlen érték hisztogramjára
Hasonló ötletek
A hisztogram egyike a minőségellenőrzés hét alapvető eszközének, amelyek közé tartozik még a Pareto-diagram, az ellenőrző lap, az ellenőrző diagram, az ok-okozati diagram, a folyamatábra és a szórásdiagram.
A hisztogram általánosítása a kernel simítási technikák. Ez egy sima valószínűségi sűrűségfüggvényt konstruál a megadott adatokból.
Kérdések és válaszok
K: Mi az a hisztogram?
V: A hisztogram egy olyan grafikus megjelenítés, amely az érintett minták eloszlásáról árulkodik.
K: Mi a célja a hisztogramnak?
V: A hisztogram célja, hogy megmutassa az érintett minták eloszlását.
K: Mit jelent a hisztogram szó?
V: A hisztogram szó a görög histos és gramma szóból származik. A hisztosz hálót vagy árbocot jelent. A gramma rajzot, feljegyzést vagy írást jelent.
K: Mit jelent a hisztosz kifejezés görögül?
V: A "hisztosz" kifejezés görögül hálót vagy árbocot jelent.
K: Mit jelent a "gramma" kifejezés görögül?
V: A "gramma" kifejezés görögül rajzot, feljegyzést vagy írást jelent.
K: Mi a hisztogram közös jellemzője?
V: A hisztogram közös jellemzője a sok kategóriát tartalmazó táblázatból készített kép.
K: Milyen információt szolgáltat egy hisztogram táblázat?
V: Egy hisztogram-táblázat információt nyújt arról, hogy hány minta van az egyes kategóriákban.
