Ellipszis: definíció, egyenlet, fókuszok és gyakorlati példák
Ellipszis: teljes útmutató — definíció, képletek és egyenlet, fókuszok, rajzolási módszerek és gyakorlati példák (bolygópályák, szerkesztés). Gyors magyarázat és gyakorló feladatok.
Az ellipszis egy olyan alakzat, amely úgy néz ki, mint egy ovális vagy lapított kör.
A geometriában az ellipszis olyan síkbeli görbe, amely egy kúp és egy sík metszéspontjából adódik úgy, hogy zárt görbét eredményez.
A körök az ellipszisek speciális esetei, amelyeket akkor kapunk, ha a vágási sík merőleges a kúp tengelyére. Az ellipszis a sík azon pontjainak a helyét is jelenti, amelyek távolsága két fix ponttól ugyanahhoz a konstanshoz adódik.
A körnek egy középpontja van, amit fókusznak nevezünk, de az ellipszisnek két fókuszpontja van.
Az ellipszis egyszerűen a grafikon minden olyan pontja, amelynél a 2 pont távolságának összege megegyezik. Egy ellipszist például úgy lehet létrehozni, hogy két tűt kartonpapírba szúrunk, és e kettő köré egy zsinórt húzunk, majd egy ceruzát teszünk a hurokba, és a lehető legmesszebbre húzzuk anélkül, hogy a zsinór minden irányban elszakadna. A bolygók pályája ellipszis, amelynek egyik fókuszában a Nap van, a másikban pedig semmi.
Az ellipszis egyenlete : ( x - h ) 2 a 2 + ( y - k ) 2 b 2 = 1 {\displaystyle {\frac {(x-h)^{2}}{a^{2}}}+{\frac {(y-k)^{2}}}{b^{2}}}=1}
ahol az ellipszis középpontja (h,k).
2A a hosszabbik vékonyabb oldal
mindkét végétől számított hossz. 2b a rövidebb oldal 2 végétől számított hossz. A²-B²=C², mert c a fókuszok és a középpont közötti hossz.
Definíció röviden
Formálisan az ellipszis az a síkbeli görbe, amelynek minden pontjára teljesül, hogy két adott ponttól (fókuszok) mért távolságok összege állandó: d(P,F1) + d(P,F2) = 2a, ahol 2a az ellipszis nagy tengelyének hossza. Ez a tulajdonság adja a gyakorlati "zsínór és tűk" módszer (gardener's method) alapját.
Standard (kanonikus) egyenlet
Ha az ellipszis középpontja a (h,k) pontban van és vízszintes irányú a nagy tengelye, akkor az egyenlete:
(x − h)² / a² + (y − k)² / b² = 1
Itt a és b pozitív számok; általában a ≥ b, és 2a a nagy (hosszabb) tengely teljes hossza, 2b a kis (rövidebb) tengely teljes hossza. (Ha a < b, akkor az ellipszis „függőlegesebb”, és a nagy tengely a y irányban van — ekkor a jelölést célszerű átváltani úgy, hogy a mindig a nagy fél-tengely legyen.)
Fókuszok, csúcsok, c és excentricitás
- Csúcsok (vertices): a középponttól a nagy tengely mentén távolságra: (h ± a, k) vízszintes esetén; vagy (h, k ± a) függőleges esetén.
- Fókuszok: a két fókusz távolsága a középponttól c, ahol c-t a következő kapcsolat adja: c² = a² − b². Így a fókuszok vízszintes esetén: (h ± c, k); függőleges esetén: (h, k ± c).
- Excentricitás: e = c / a. Az excentricitás 0 és 1 közötti szám, ahol e = 0 kört ad (ha a = b), és e közeledik 1-hez, az ellipszis szálasabbá válik.
Méret és terület
- Teljes tengelyhosszak: nagy tengely = 2a, kis tengely = 2b.
- Terület: A = π · a · b.
- Kerület (megközelítő): az ellipszis kerületének nincs egyszerű elemi alakja; jó közelítés Ramanujan első közelítése: P ≈ π [3(a + b) − sqrt((3a + b)(a + 3b))].
Az egyenletből a geometriai adatok meghatározása
- Ha adott az egyenlet formája (x − h)²/a² + (y − k)²/b² = 1 és tudjuk, hogy a ≥ b, akkor: nagy fél-tengely = a, kis fél-tengely = b, c = sqrt(a² − b²), fókuszok: (h ± c, k).
- Ha az egyenlet általános másodfokú alakban van: Ax² + Bxy + Cy² + Dx + Ey + F = 0, akkor a konikus egy kis vizsgálattal eldönthető: B² − 4AC < 0 esetén a görbe (valós) ellipszis (ha egyáltalán valós pontjai vannak). A forgatott ellipszis egyenletét forgatással (koordinátatranszformációval) tudjuk kanonikus alakra hozni.
Gyakorlati példák és alkalmazások
- Gardener's construction (zsínór és tűk): A két tű kijelöli a fókuszokat; a zsinór hossza 2a; a ceruzát mozgatva az összetartó zsinór végig az ellipszist rajzolja. Ez szemlélteti a definíciót: a fókuszoktól mért távolságok összege állandó.
- Bolygómozgás: Kepler első törvénye szerint a bolygók pályája ellipszis, amelynek egyik fókuszában a Nap található.
- Műszaki és optikai alkalmazások: reflektorok, hang- és fényvisszaverő rendszerek (pl. akusztikus tükrök), ahol a fókuszok tulajdonságát használják ki.
Tippek feladatokhoz
- Ha egy adott pont P és két fókusz F1, F2 ismertek, ellenőrizd, hogy d(P,F1) + d(P,F2) = 2a teljesül-e.
- Ha kapott egyenletet kell értelmezni, először rendezd kanonikus formára (kitűzve a középpontot), majd azonosítsd a paramétereket a, b és c segítségével.
- Kerület számításnál használj Ramanujan-közelítést, ha pontos integrál nyújtása bonyolultnak bizonyul.
Ha szeretnéd, megmutatom egy konkrét példán, hogyan számoljuk ki az ellipszis fókuszait és excentricitását egy adott egyenletből — küldd el az egyenletet (vagy a paramétereket a, b, h, k értékeit) és kiszámolom!
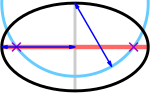
A fókuszok (lila keresztek) a főtengely (piros) és egy olyan kör (ciánkék) metszéspontjában vannak, amelynek sugara megegyezik a félnagytengellyel (kék), és amelynek középpontja a melléktengely (szürke) egyik végpontja.

Egy kúp és egy sík metszéspontjaként kapott ellipszis.
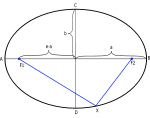
Egy ellipszis és tulajdonságai.
Kérdések és válaszok
K: Mi az az ellipszis?
V: Az ellipszis egy olyan alakzat, amely úgy néz ki, mint egy ovális vagy lapított kör. A geometriában egy síkbeli görbe, amely egy kúp és egy sík metszéspontjából adódik úgy, hogy egy zárt görbét eredményez.
K: Hogyan lehet ellipszist létrehozni?
V: Ellipszist úgy lehet készíteni, hogy két tűt kartonpapírba szúrunk, majd a két tű köré hurkot húzunk, majd a hurokba ceruzát teszünk, és a lehető legmesszebbre húzzuk anélkül, hogy a húr minden irányban elszakadna.
K: Melyek a körök speciális esetei?
V: A körök az ellipszisek speciális esetei, amelyek akkor jönnek létre, ha a vágási sík merőleges a kúp tengelyére.
K: Hány fókuszpontja van egy ellipszisnek?
V: Az ellipszisnek két fókuszpontja van.
K: Milyen egyenlet írja le az ellipszist?
V: Az ellipszis egyenlete: (x - h)²/a² + (y - k)²/b² = 1, ahol h és k az ellipszis középpontját jelöli, 2a pedig a hosszabb, vékonyabb oldalának mindkét végétől mért hosszat, míg 2b a rövidebb oldalának mindkét vége közötti hosszat. C az ellipszis fókuszpontja és középpontja közötti hosszat jelenti, úgy, hogy A²-B²=C².
K: Hol látunk példákat elliptikus pályákra?
V: Elliptikus pályákat láthatunk a bolygókon, amelyek egyik fókuszpontjában a nap van.
Keres
