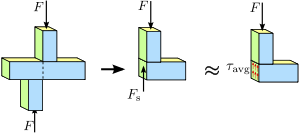Feszültség (mechanika) - definíció, képlet és SI-egység
Feszültség (mechanika): definíció, σ = F/A képlet és SI‑egység (Pa) egyszerű magyarázattal, gyakorlati példákkal és alkalmazásokkal.
Definíció
A feszültség (mechanikában) az egységnyi területre jutó erő, amely egy anyagot alakváltozásra késztet. Más megközelítésben a feszültség egy testben a részecskék közötti belső erők mérőszáma: ezek a belső erők a testre ható külső erőkre adott reakciók, amelyek a testet szétválasztják, összenyomják vagy elcsúsztatják. A külső erők lehetnek felületi erők vagy testerők. A feszültség tehát az az átlagos erő, amelyet a test egyik részecskéje a szomszédos részecskére gyakorol egy képzeletbeli elválasztó felületen keresztül.
Képlet (egytengelyű normálfeszültség)
Egyszerű esetben, ha egy szakaszt egyenlően terhelnek tengelyirányú erővel, az egytengelyű normálfeszültség képlete:
σ = F A {\displaystyle {\sigma }={\frac {F}{A}}}
ahol σ a feszültség, F az erő, és A a keresztmetszeti felület.
Fontos megjegyezni, hogy ez az egyszerű képlet átlagos (átlagolt) értéket ad: valódi szerkezetekben a feszültség helyileg változhat a geometriától, anyaghibáktól vagy terhelésirányoktól függően.
Feszültségtípusok
- Normálfeszültség: a felületre merőleges erő okozza (húzó vagy nyomó).
- Nyírófeszültség: a felület mentén eltoló erő okozza (síktartó elcsúszás).
- Torziós, hajlító és kombinált feszültségek: valós szerkezetekben többfajta feszültség egyszerre lehet jelen.
Feszültség mint tenzor
Általános háromdimenziós esetben a feszültség pontonként és irányonként jellemzendő: ilyenkor a feszültség egy másodrendű tenzor, gyakran σij jelöléssel. A tenzor elemei megadják, hogy az i-edik irány felületén milyen j-irányú erő hat. A tenzornak valódi előnye, hogy lehetővé teszi a főfeszültségek (principal stresses) meghatározását, valamint a nyíró- és normálkomponensek szétválasztását.
SI-egység és mértékegységek
Az SI-rendszerben az erőt newtonban (N), a területet pedig négyzetméterben (m²) mérik. Ennek megfelelően a feszültség egysége N/m². A feszültségnek azonban saját SI-egysége van, a pascal (Pa):
- 1 Pa = 1 N/m²
- Gyakrabban használt alakok: kPa (kilopascal), MPa (megapascal), GPa (gigapascal).
- Az angolszász mértékegységekben a feszültséget gyakran font-erő/négyzet hüvelykben mérik (psi).
- Átváltás: 1 MPa = 106 Pa ≈ 145 psi (megközelítőleg).
A feszültség dimenziója megegyezik a nyomáséval, ezért a két fogalom matematikailag azonos dimenziós, bár fizikailag és alkalmazásukban különbségek lehetnek (pl. nyomás általában folyadékokra és gázokra, feszültség szilárd testekre vonatkozik).
Kontinuummechanika és feszültségeloszlás
A kontinuummechanikában a terhelt, deformálódó testet kontinuumként kezeljük: a belső erők és így a feszültség folyamatosan oszlanak el az anyagtérfogatban. Ez azt jelenti, hogy a feszültségeloszlást a tér és az idő folyamatos függvényeként írjuk le (a cikk eredeti megfogalmazása szerint: darabosan folytonos — a lényeg az, hogy pontonként definiálható).
Az erők a test alakjának deformációját okozzák. Az alakváltozás mértékét a deformációs tenzor (pl. húzási alakváltozás ε) adja meg, és lineáris rugalmas anyagoknál a feszültség és az alakváltozás között Hooke törvénye írja le az összefüggést, például egytengelyű esetben σ = E·ε, ahol E a rugalmassági modulus.
Ha az anyag nem elég szilárd, a túl nagy feszültség tartós alakváltozáshoz (képlékeny alakváltozás) vagy szerkezeti tönkremenetelhez vezethet (anyag meghibásodása). A geometriai tényezők és lokális hatások (pl. élkörnyezet, bevágások, furatok) erősen befolyásolják a helyi feszültségeloszlást és így a hibakockázatot.
Gyakorlati megjegyzések
- Átlagos vs. helyi feszültség: Az egyszerű σ = F/A képlet átlagos feszültséget ad; például élsugár, kulcslyuk-él, vagy anyaghibák környezetében a feszültség lokálisan jóval nagyobb lehet (feszültségkoncentráció).
- Jelölés és előjelszabályok: Húzófeszültséget gyakran pozitívnak, nyomófeszültséget negatívnak tekintik — ez a konvenció alkalmazásonként eltérhet.
- Mérések: Feszültséget közvetetten mérnek pl. nyúlásmérő bélyegekkel (strain gauge), amely a lokális alakváltozást méri, és Hooke-törvény alapján feszültségre konvertálható.
- Szabványok és határértékek: Szerkezeti anyagokra vonatkozó tervezési szabványok megadják az elfogadható feszültségértékeket (pl. engedélyezett feszültség, szakító- és folyáshatár értékek).
Összefoglalás
A feszültség alapfogalom a szerkezetek viselkedésének megértésében: megmutatja, hogy mekkora belső erők hatnak egy anyagon belül egységnyi területen. Az egyszerű képletek (σ = F/A) hasznosak, de a valós tervezésnél figyelembe kell venni a feszültségtenzor háromdimenziós természetét, a helyi koncentrációkat, az anyag viselkedését és a geometria hatásait.
1.4. ábra Nyírófeszültség egy prizmás rúdban. A rúd keresztmetszetében a feszültség vagy az erő eloszlása nem feltétlenül egyenletes. Ennek ellenére egy átlagos nyírófeszültség τ a v g {\displaystyle \tau _{\mathrm {avg} }\,\! }
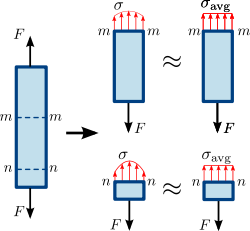
1.3. ábra Normálfeszültség egy prizmás (egyenes, egyenletes keresztmetszetű) rúdban. A rúd keresztmetszetében a feszültség- vagy erőeloszlás nem feltétlenül egyenletes. Azonban egy átlagos normálfeszültség σ a v g {\displaystyle \sigma _{\mathrm {avg} }\,\! }
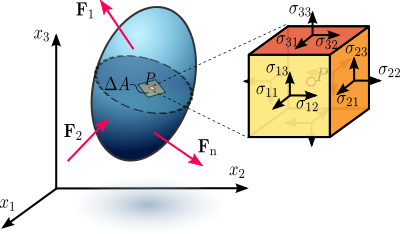
1.1. ábra Feszültség egy terhelt deformálható anyagtestben, amelyet kontinuumnak tekintenek.
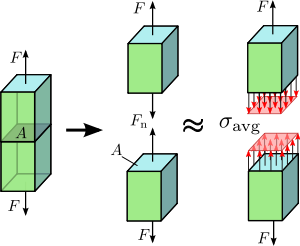
1.2. ábra Axiális feszültség egy tengelyirányban terhelt prizmás rúdban.
Nyírófeszültség
További információk: Nyírófeszültség
Egyszerű feszültségek
Bizonyos helyzetekben a tárgyon belüli feszültséget egyetlen számmal vagy egyetlen vektorral (egy szám és egy irány) lehet leírni. Három ilyen egyszerű feszültséghelyzet az egytengelyű normálfeszültség, az egyszerű nyírófeszültség és az izotróp normálfeszültség.
Egytengelyű normálfeszültség
A húzófeszültség (vagy feszültség) az a feszültségállapot, amely táguláshoz vezet, azaz az anyag hossza a húzó irányban növekszik. Az anyag térfogata állandó marad. Ha egy testre egyenlő és ellentétes erő hat, akkor az ebből az erőből eredő feszültséget húzófeszültségnek nevezzük.
Ezért egy egytengelyű anyagban a hossz a húzófeszültség irányában nő, a másik két irányban pedig csökken. Az egytengelyű feszültségmódban a húzófeszültséget húzóerők idézik elő. A húzófeszültség a nyomófeszültség ellentéte.
Közvetlen feszültség alatt álló szerkezeti elemek a kötelek, talajhorgonyok és szögek, csavarok stb. A hajlítónyomatékoknak kitett gerendákhoz tartozhat húzófeszültség, valamint nyomófeszültség és/vagy nyírófeszültség is.
A szakítófeszültség a szakítószilárdság, azaz a feszültség határállapotának eléréséig növelhető.
Feszültség egydimenziós testekben
Minden valós tárgy háromdimenziós teret foglal el. Ha azonban két dimenzió nagyon nagy vagy nagyon kicsi a többihez képest, akkor a tárgyat egydimenziósnak lehet modellezni. Ez leegyszerűsíti a tárgy matematikai modellezését. Az egydimenziós tárgyak közé tartozik egy darab drót, amelyet a végeinél megterhelnek és oldalról néznek, valamint egy fémlemez, amelyet az oldalán terhelnek és közelről és a keresztmetszetén keresztül néznek.
Kapcsolódó oldalak
- Feszültség
- Hajlítás
Kérdések és válaszok
K: Mi a stressz?
V: A stressz az egységnyi területre jutó erő egy testre, amely az alakváltozást idézi elő. Egy testben a részecskéi között fellépő belső erők mérőszáma, és az az egységnyi területre jutó átlagos erő, amelyet egy test egy részecskéje a szomszédos részecskére gyakorol az őket elválasztó képzeletbeli felületen keresztül.
K: Hogyan befolyásolják a külső erők a feszültséget?
V: A külső erők vagy felületi erők, vagy testerők, és a test alakjának deformációját okozzák, ami tartós alakváltozáshoz vagy szerkezeti tönkremenetelhez vezethet, ha az anyag nem elég erős.
K: Mi az egytengelyű normálfeszültség képlete?
V: Az egytengelyű normálfeszültség képlete σ = F/A, ahol σ a feszültség, F az erő és A a felület. Az SI-egységekben az erőt newtonban, a területet pedig négyzetméterben mérik, vagyis a feszültség newton per négyzetméter (N/m2). A feszültségnek azonban létezik saját SI-egysége, a pascal (Pa), amely 1 N/m2 -nek felel meg. Császári mértékegységben a feszültséget font-erő/négyzetcentiméterben (psi) mérnénk.
K: Mit feltételez a kontinuummechanika az erőről?
V: A kontinuummechanika klasszikus modelljei átlagos erőt feltételeznek, és nem veszik megfelelően figyelembe a geometriai tényezőket - vagyis nem veszik figyelembe, hogy a geometria hogyan befolyásolja az energia felépülését a külső erő alkalmazása során.
K: Hogyan adhatnak különböző modellek eltérő eredményeket az anyag és a szilárd testek deformációjának vizsgálatakor?
V: A különböző modellek különbözőképpen vizsgálják az anyag és a szilárd testek deformációját, mivel az anyag és a szilárd testek jellemzői háromdimenziósak - így minden megközelítés más-más szempontokat vesz figyelembe, ami eltérő eredményekhez vezethet.
K: Hogyan kezeli a kontinuummechanika a terhelt deformálódó testeket?
V: A kontinuummechanika a terhelt deformálódó testeket kontinuumként kezeli - ami azt jelenti, hogy a belső erők folyamatosan oszlanak el az anyagi test térfogatán belül, ahelyett, hogy a klasszikus modellekhez hasonlóan bizonyos pontokra koncentrálódnának.
Keres