Erőnyomaték (pillanat) – fizikai definíció, képlet és példák
Erőnyomaték (pillanat) — definíció, képlet és gyakorlati példák: számítások, SI‑egység (Nm) és mindennapi alkalmazások (ajtó, csiga, fogaskerék).
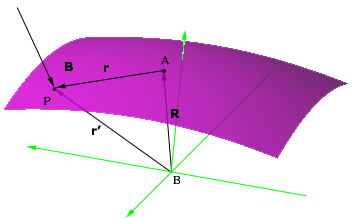
A fizikában az erőnyomaték (gyakran csak pillanat) annak a tendenciának a mértéke, hogy egy testet egy adott pont vagy tengely körül forgásba hoz. Ez a fogalom leírja, mekkora „forgatóhatást” fejt ki egy adott erő, figyelembe véve az erő alkalmazásának helyét a forgástengelyhez képest.
Mi határozza meg az erőnyomatékot?
Az erőnyomaték két tényezőtől függ:
- az erő nagyságától (F), és
- a nyomatékkartól vagy más néven a merőleges távolságtól (r⊥) — ez a forgástengelytől az erő hatásvonaláig mért merőleges távolság.
Vektoros formában a nyomaték a helyvektor és az erő vektoriális szorzata: τ = r × F. Ennek nagysága: τ = r F sinθ, ahol θ az r és F közötti szög. Gyakran egyszerűsítve használjuk a skaláris alakot:
Momentum = Erő × merőleges távolság {\displaystyle {\text{Momentum}}={\text{Erő}}\szor {\text{Merőleges távolság}}}
Egység és jelölés
Az erőnyomaték SI-mértékegysége a newtonméter (N·m). Ezt a dimenziót tekintve kg·m²/s²-vel is felírhatjuk (azonos dimenziója van a joule-nak, de fizikailag más mennyiségről van szó: a nyomaték forgatóhatást, a joule energiát jelent).
Statika: a pillanatok egyensúlya
Statikai egyensúly esetén a testre ható forgató (forgatónyomaték) hatások összege nulla. Gyakran ezt így fogalmazzuk meg: az óramutató járásával megegyező irányú pillanatok összege megegyezik az ellentétes irányú pillanatok összegével, vagy algebrailag: Στ = 0. Ez az elv lehetővé teszi szerkezetek és egyszerű gépek tervezését és elemzését.
Példák és alkalmazások
- Ajtó nyitása: egy kilincshez közelebb ható erő kisebb nyomatékot eredményez, mint egy széles ajtón alkalmazott ugyanakkora erő — ezért érdemes a kilincset az ajtó pereméhez közel elhelyezni.
- Csavarhúzó és csőkulcs: hosszabb fogó (nagyobb kar) kisebb erővel tud nagyobb nyomatékot létrehozni.
- Emelők és karok: csörlők, fogaskerekek és hasonló egyszerű gépek mind a nyomatékváltás elvén működnek, mechanikai előnyt biztosítva.
- Autómotor: a forgatónyomaték (torque) jellemzi, milyen erővel képes a motor forgatni a hajtást; a teljesítmény és a nyomaték összefügg az fordulatszámmal.
Gyakorlati számítási példa
Tegyük fel, hogy egy csőkulccsal 50 N erőt alkalmazunk, a kötőelemet 0,3 m távolságra fogva (az erő merőleges a kulcsra). A nyomaték:
τ = F × r = 50 N × 0,3 m = 15 N·m.
Ha az erő nem merőleges a karra, és például 30°-os szöget zár be a karral, akkor a merőleges komponens F⊥ = F sin30° = 50 N × 0,5 = 25 N, így τ = 25 N × 0,3 m = 7,5 N·m.
Kapcsolat a forgómozgással
A dinamikában az erőnyomaték a forgó testek gyorsulását okozza: τ = I α, ahol I a tehetetlenségi nyomaték (moment of inertia), α pedig a szögletes gyorsulás. Fontos megkülönböztetni a pillanatot (erő × távolság) és a tehetetlenségi nyomatékot (a tömegeloszlás miatti ellenállás a forgásnak) —bár mindkettőben szerepel a „nyomaték” szó, fizikailag különböző fogalmak.
Összefoglalás
Az erőnyomaték (pillanat) egyszerű, de kulcsfontosságú mennyiség a mechanikában: megmutatja, milyen hatékonysággal képes egy erő forgatni egy testet a forgástengely körül. A számításához ismerni kell az erőt és annak a forgástengelytől mért merőleges távolságát, továbbá figyelni kell az irányokra és előjellel történő összeadásokra, különösen statikai feladatoknál.
A nyomatékra példa: csörlőkarok, ajtók nyitása és zárása, diótörők, konzervnyitók és feszítővasak mind a karhossz változtatásával hoznak létre mechanikai előnyt.
A kar mint egyszerű gép lényege, hogy egy erő (erőkifejtés) segítségével egy másik erőt (terhelés) leküzdhessünk; a hatékonyságát a karok hosszának és az alkalmazott erők viszonyai határozzák meg. A fizikában a pillanat egy fizikai mennyiség és egy távolság kombinációja, amely a forgatóhatást kvantitatívan jellemzi.
A pillanat története
A nyomatékok elve Archimédesznek a kar működési elvére vonatkozó felfedezéséből származik. A karban az ember egy erőt, az ő idejében leggyakrabban emberi izmot, egy karra, valamilyen gerendára alkalmaz. Arkhimédész megjegyezte, hogy a tárgyra kifejtett erő nagyságát, az erőnyomatékot a következő módon határozzuk meg: M = rF, ahol F az alkalmazott erő, r pedig az alkalmazott erő és a tárgy közötti távolság.
Kérdések és válaszok
K: Mi a hatalom pillanata?
V: Az erőnyomaték, amelyet gyakran egyszerűen csak nyomatéknak neveznek, annak a tendenciának a mértéke, hogy egy erő egy tárgyat egy adott pont vagy tengely körül forgásba hoz.
K: Milyen szerepet játszik a pillanatnyi kar ebben a koncepcióban?
V: A nyomatékkar a forgástengelytől való távolság, és fontos szerepet játszik ebben a koncepcióban. Az egyszerű gépek, mint például a karok, csigák és fogaskerekek a nyomatékkar megváltoztatásával mechanikai előnyt hoznak létre.
K: Mi a nyomaték SI-egysége?
V: A nyomatékok SI-egysége a newtonméter (kgm²/s²).
K: Mi a képlet a momentumok kiszámítására?
V: A nyomatékok kiszámításának képlete a következő: Momentum = Erő × merőleges távolság.
K: Milyen elv érvényesül a pillanatok mérlegelésekor?
V: A momentumok elve azt mondja ki, hogy amikor egy rendszer egyensúlyban van, az óramutató járásával megegyező irányú momentumok összegének meg kell egyeznie az óramutató járásával ellentétes irányú momentumok összegével.
K: Hol vannak példák arra, hogy hol alkalmazhatók a pillanatok?
V: Példák arra, ahol a pillanatokat (fordított hatás) alkalmazzák, a karok, például a lengőkarok, az ajtók nyitása és zárása, a diótörők, a konzervnyitók és a feszítővasak.
K: Hogyan működnek a karok az erők és a távolságok szempontjából?
A: A kar úgy működik, hogy egy erő, az úgynevezett erőkifejtés segítségével legyőz egy másik erőt, az úgynevezett terhelést. A fizikában a pillanat egy fizikai mennyiséget és egy távolságot is magában foglal.
Keres
