Párhuzamossági posztulátum (Euklidesz ötödik posztulátuma) — definíció
Ismerd meg a párhuzamossági posztulátum (Eukleidész 5.) definícióját, magyarázatát és következményeit az euklideszi és nem-euklideszi geometriában.
A geometriában a párhuzamossági posztulátum az euklideszi geometria egyik alapvető axiómája. Gyakran Eukleidész ötödik posztulátumának is nevezik, mivel ez az ötödik posztulátum szerepel Eukleidész Elemek című művében. A posztulátum megfogalmazása és következményei különösen fontosak a geometria alapjai és a különböző geometriák közötti különbségek megértéséhez.
Megfogalmazás
A posztulátum egyik hagyományos megfogalmazása a következő:
Ha egy egyenes szakaszt két egyenessel vágunk el, és a két belső szög, amelyet a vonalak alkotnak, kisebb, mint 180°, akkor a két egyenes végül találkozni fog, ha elég hosszúra nyújtjuk őket.
Gyakran használják helyette a rövidebb, ekvivalens változatot, az ún. Playfair-tételt:
Adott egy egyenes és az azon kívüli egy pont; legfeljebb egy vele párhuzamos egyenes húzható ezen a ponton át.
Ekvivalens állítások és következmények
- Playfair axiómája (fenti rövid megfogalmazás) a többi euklideszi axiómaval együtt pontosan ekvivalens Euklidész ötödik posztulátumával.
- A posztulátum fontos következményei közé tartozik, hogy egy háromszög belső szögeinek összege 180° (egy sík háromszögeiben), valamint hogy egy egyeneshez adott ponton át pontosan egy vele párhuzamos egyenes létezik.
- Sok gyakori geometriai tény (például a hasonlóságok általános elmélete, a trapéz és bizonyos téglalap-tulajdonságok) a párhuzamossági posztulátum használatát igényli.
Történeti és matematikai jelentőség
Eukleidész maga nem adott független bizonyítékot az ötödik posztulátumra; több száz éven át számos matematikus próbálta bebizonyítani, hogy az valóban következik az első négy posztulátumból. A 19. században azonban kiderült, hogy ez nem lehetséges: sokan, köztük Gauss, Bolyai és Lobacsevszkij, független utakat találtak a párhuzamossági posztulátumtól eltérő, de belsőleg következetes geometriák felépítésére.
Nem-euklideszi geometriák — modellek és következmények
Az ötödik posztulátum függetlenségét több modell is illusztrálja:
- Hiperbolikus geometria (Lobacsevszkij, Bolyai): itt egy adott egyeneshez az azon kívüli pontból végtelen sok párhuzamos (azaz nem metsző) egyenes húzható; a háromszög szögeinek összege kevesebb, mint 180°.
- Elliptikus geometria (például a gömbi geometria megfelelő átalakítása): itt nincs olyan egyenes, amely párhuzamos lenne egy adott egyenessel — minden egyenes minden másikat metszi; a háromszög szögeinek összege nagyobb, mint 180°.
- Konkrét modelleket adtak a hiperbolikus geometriára: Beltrami, Klein és Poincaré-féle modellek megmutatták, hogy a nem-euklideszi geometriák belsőleg következetesek, ha az euklideszi geometria következetes.
Az abszolút geometria
A geometria azon része, amely csak Euklidész első négy axiómáját használja, abszolút geometriaként vagy semleges geometriaként ismert. Ebben a keretben számos tétel igaz mind az euklideszi, mind a hiperbolikus geometriában, de a párhuzamossági posztulátumra épülő állítások (például a háromszög szögösszegének pontos 180°-a) nem következnek belőle.
Összefoglalás
A párhuzamossági posztulátum (Euklidesz ötödik posztulátuma) jelenti az egyik legfontosabb választóvonalat az euklideszi és a nem-euklideszi geometriák között. Megfogalmazása, ekvivalens változatai (például Playfair axiómája), története és a belőle/lehet tőle eltérő geometriai modellek mind alapvető szerepet játszanak a geometria elméleti fejlődésében. Azokat a geometriákat, amelyek követik Euklidész összes axiómáját, továbbra is euklideszi geometriának nevezzük, míg azokat, amelyek nem követik Euklidész összes axiómáját, nem-euklideszi geometriának hívjuk.
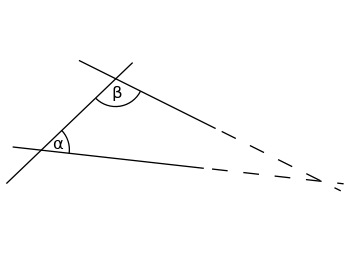
Ha az α (alfa) és β (béta) belső szögek összege kisebb, mint 180°, akkor a két egyenes valahol metszeni fogja egymást, ha mindkettő a végtelenbe nyúlik.
Történelem
Egyes matematikusok úgy gondolták, hogy Euklidész ötödik posztulátuma sokkal hosszabb és bonyolultabb, mint a másik négy posztulátum. Sokan közülük úgy gondolták, hogy ez a többi egyszerűbb axiómából is bizonyítható. Néhány matematikus bejelentette, hogy az egyszerűbb tételekből bebizonyította a tételt, de mindannyian tévedtek.
Playfair axiómája
Egy másik, újabb keletű tétel, amelyet Playfair axiómaként ismerünk, hasonló Euklidész ötödik posztulátumához. Eszerint:
Adott egy egyenes és egy pont, amely nem ezen az egyenesen van, csak egy olyan egyenest lehet húzni ezen a ponton keresztül, amely nem találkozik a másik egyenessel.
Valójában a matematikusok rájöttek, hogy ez az axióma nemcsak hasonlít Euklidész ötödik posztulátumához, hanem pontosan ugyanazokat a következményeket vonja maga után. Matematikailag a két tételt "ekvivalens" tételeknek nevezik. Manapság Playfair axiómáját gyakrabban használják a matematikusok, mint Euklidész eredeti párhuzamos posztulátumát.
Nem-euklideszi geometria
Végül néhány matematikus megpróbált új geometriákat építeni az axióma használata nélkül. A nem-euklideszi geometria egyik fajtáját elliptikus geometriának nevezik. Az elliptikus geometriában a párhuzamos posztulátumot egy axióma helyettesíti, amely kimondja, hogy:
Adott egy egyenes és egy pont, amely nem ezen az egyenesen van, nem lehet olyan egyenest húzni ezen a ponton keresztül, amely végül nem keresztezi a másik egyenest.
A matematikusok rájöttek, hogy amikor Euklidész ötödik tételét ezzel az axiómával helyettesítették, még mindig képesek voltak bizonyítani Euklidész számos más tételét. Az elliptikus geometria elképzelésének egyik módja, ha egy földgömb felszínére gondolunk. A földgömbön a hosszúsági vonalak az egyenlítőnél párhuzamosnak tűnnek, de a sarkoknál mind találkoznak. A 19. század végén az elliptikus geometria következetesnek bizonyult. Ez bebizonyította, hogy Euklidész ötödik tételének érvényessége nem független a többi tételétől. Ezt követően a matematikusok többnyire felhagytak azzal, hogy az ötödik posztulátumot a másik négy posztulátumból próbálják bizonyítani. Ehelyett sok matematikus más geometriákat kezdett tanulmányozni, amelyek nem követik Euklidész ötödik posztulátumát.
Egy másik axióma, amellyel a matematikusok néha Euklidész ötödik axiómáját helyettesítik, így szól:
Adott egy egyenes és egy pont, amely nem ezen az egyenesen van, legalább két olyan egyenest tudsz rajzolni ezen a ponton keresztül, amely végül nem keresztezi a másik egyenest.
Ezt nevezzük hiperbolikus geometriának.
Egy másik geometria egyszerűen eltávolítja Euklidész ötödik posztulátumát, és nem helyettesíti azt semmivel. Ezt nevezik semleges geometriának vagy abszolút geometriának.
Keres