Minkowski-téridő: a speciális relativitás négydimenziós térideje
Minkowski-téridő: áttekintő, érthető magyarázat a speciális relativitás négydimenziós téridejéről, metrikáról, idő- és térdimenziók kapcsolatáról.
A speciális relativitáselméletben a Minkowski-téridő egy négydimenziós sokaság, amelyet Hermann Minkowski alkotott meg. Négy dimenziója van: három térdimenzió (x, y, z) és egy idődimenzió. A Minkowski-téridő metrikus szignatúrája (-+++), és sík felületet ír le, ha nincs tömeg. Ebben a cikkben a Minkowski-téridőt egyszerűen téridőnek nevezzük.
A Minkowski-téridő azonban csak a speciális relativitáselméletben érvényes. Az általános relativitáselmélet a görbült téridő fogalmát használta a gravitáció és a gyorsított mozgás hatásainak leírására.
Alapfogalmak és metrika
A Minkowski-téridőn a távolságot az ún. invariáns időtérintervallum (vagy egyszerűen intervalum) méri. A vonalelem (line element) általános alakja sík Minkowski-térben:
ds2 = -c2 dt2 + dx2 + dy2 + dz2,
ahol c a fénysebesség. Gyakran egységben választják c = 1-et, így a kifejezés egyszerűbb lesz. A metrikát mátrixos formában az ημν = diag(-1, 1, 1, 1) adja meg (ez a -+++ konvenció). Más irodalmakban előfordul a +--- választás is; a fizikai eredmények ettől nem változnak, csak előjelek és jelölések módosulnak.
Idő, proper idő és invarancia
Az intervalum invariáns minden inerciarendszer között: két esemény közötti ds2 értéke minden Lorentz-transzformáció után ugyanaz marad. Az időtartam, amelyet egy mozgó órán ez alatt az eseménypár alatt mérnek, a proper idő τ, és timelike (időszerű) intervallum esetén:
dτ2 = - (1/c2) ds2,
ami a híres idődilatációhoz vezet: egy mozgó órát egy nyugvó megfigyelő a Lorentz-faktorral γ = 1/√(1 − v2/c2) lelassítva lát (Δt = γ Δτ).
Fénykúp, kauzalitás és elválasztás
A Minkowski-téridőben minden eseményhez hozzátartozik egy fénykúp, amely megadja, hogy mely események lehetnek kauzálisan kapcsolódva hozzá. Három eshetőség:
- Timelike (ds2 < 0): két esemény között létezhet ok-okozati kapcsolat; van olyan test, amely mindkettőn átmehet.
- Lightlike / null (ds2 = 0): az eseményeket fény vagy más null-sebességű jel köti össze; a kapcsolat sebessége pontosan c.
- Spacelike (ds2 > 0): nincs kauzális kapcsolat; különböző inercia-megfigyelők más sorrendet láthatnak ezekben az eseményekben (relativitás elve a szimultaneitásról).
Lorentz-transzformációk és inercia
A speciális relativitás inertiarendszerei között a kapcsolatot a Lorentz-transzformációk adják, amelyek megőrzik az intervalumot. Egy egyszerű egyirányú mozgás (x tengely mentén) esetén a transzformáció:
x' = γ (x − v t),
t' = γ (t − v x / c2),
ahol γ a Lorentz-faktor. Ezek a transzformációk eredményezik a klasszikus effektusokat, mint a Lorentz-összehúzódás (length contraction) és idődilatáció (time dilation), valamint a relativisztikus összeadódás szabályát a sebességekhez.
Négyvektorok, négysebesség és energia-impulzus
Az eseményeket és mozgásokat négyvektorokkal írjuk le: az esemény koordinátái Xμ = (ct, x, y, z). A részecskék mozgásához tartozó négysebesség és négyimpulzus hasznos fogalmak:
Uμ = dXμ/dτ (négysebesség), Pμ = m Uμ (négyimpulzus),
ami az energia-impulzus kapcsolatot adja: E2 = (pc)2 + (m c2)2. A négyvektorok transzformálódnak Lorentz-transzformáció alatt, így a fizikai mennyiségek összhangban maradnak minden inercia-megfigyelő számára.
Geometriai szemlélet és ábrázolás
A Minkowski-téridőt gyakran ábrázolják két dimenzióban (ct és x tengely), ahol a fénykúp ±45°-os vonalakkal jelenik meg (c = 1 egységben). Ez segít vizualizálni a kauzalitást, a világvonalakat (egy részecske mozgása az időben) és a szimultaneitás relatív jellegét: egy adott megfigyelő számára a szimultán események egyenes vonalúnak látszanak, másik mozgó megfigyelő számára ez a vonal más meredekségű.
Kapcsolat az általános relativitással
Bár a Minkowski-téridő sík (görbületmentes), az általános relativitáselmélet a görbült téridőt használja a tömeg és energia hatásainak leírására. Lokálisan azonban bármely görbült téridő pontján található érintőteret (tangent space) Minkowski-metrikával írhatjuk le: ez tükrözi, hogy rövid léptékben a speciális relativitás törvényei érvényesek.
Összefoglalás
A Minkowski-téridő a speciális relativitás geometriai megfogalmazása: négydimenziós, sík (görbületmentes) sokaság, amelyben az idő és a tér egyesül, az intervalum invariáns marad, és a fénykúp határozza meg a kauzális kapcsolódást. Ez a keret teszi lehetővé a relativisztikus mozgások, idődilatáció, Lorentz-összefüggések és a négyvektoros szemlélet egységes leírását, miközben szolgál alapul az általános relativitáselmélet helyi alkalmazásaihoz is.
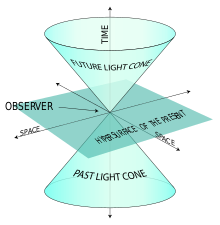
Példa egy fénykúpra.
Meghatározás(ok)
Matematikai
A téridőt négydimenziós koordinátarendszerként képzelhetjük el, amelynek tengelyei a következők szerint alakulnak
( c t , x , y , z ) {\displaystyle (ct,x,y,z)} 
Ezeket a következővel is jelölhetjük
( x 1 , x 2 , x 3 , x 4 ) {\displaystyle (x_{1},x_{2},x_{3},x_{4})} 
Ahol x 1 {\displaystyle x_{1}}
a c t {\displaystyle ct}
. Az időt azért mérjük a fénysebesség és az időkoordináta szorzatában, mert így az idő mértékegységei megegyeznek a tér mértékegységeivel. A téridő ívhosszúság differenciálegyenlete a következővel adott
d s 2 = - c 2 d t 2 + d x 2 + d y 2 + d z 2 {\displaystyle ds^{2}=-c^{2}dt^{2}+dx^{2}+dy^{2}+dz^{2}}} 
Ez azt jelenti, hogy a téridőnek van egy metrikus tenzora, amely a következővel van megadva
g u v = [ - 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 ] {\displaystyle g_{uv}={\begin{bmatrix}-1&0&0&0&0\\\0&1&0&0\\\0&0&1&0\\0&0&0&0&1\end{bmatrix}}} 
Ahogyan azt már említettük, a téridő mindenhol sík; bizonyos mértékig síknak is felfogható.
Egyszerű
A téridőt úgy lehet elképzelni, mint azt az "arénát", amelyben a világegyetem összes eseménye zajlik. A téridő egy pontjának meghatározásához csupán egy bizonyos időre és egy jellemző térbeli orientációra van szükség. A négy dimenziót nehéz (gyakorlatilag lehetetlen) szemléltetni, de az alábbi módszerrel némi analógia felállítható.
Téridő-diagramok
Hermann Minkowski bevezetett egy bizonyos módszert a Minkowski-téridőbeli koordinátarendszerek grafikus ábrázolására. Amint a jobb oldalon látható, a különböző koordinátarendszerek nem értenek egyet egy tárgy térbeli tájolásával és/vagy időbeli helyzetével kapcsolatban. Amint az ábrán látható, csak egy térbeli tengely (az x-tengely) és egy időtengely (a ct-tengely) van. Ha szükséges, bevezethetünk egy további térbeli dimenziót (az y-tengelyt); sajnos ez a dimenziók számának határa: négy dimenzióban való grafikus ábrázolás lehetetlen. A Minkowski-téridőben való grafikus ábrázolás szabálya a következő:
1) Az x-tengely és az x'-tengely közötti szöget a t a n ( α ) = v c {\displaystyle tan(\alpha )={\frac {v}{c}}}}
adja meg, ahol v a tárgy sebessége.
2) A fény sebessége a téridőn keresztül mindig 45 fokos szöget zár be bármelyik tengellyel.
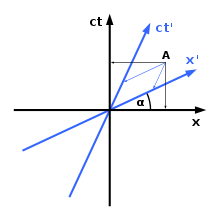
A relativitáselméletben mindkét megfigyelő más-más időponthoz rendeli az A-nál bekövetkező eseményt.
A téridő az általános relativitáselméletben
Az általános relativitáselméletben Einstein az alábbi egyenletet használta
R u v - 1 2 g u v R = 8 π T u v {\displaystyle R_{uv}-{\frac {1}{2}}g_{uv}R=8\pi T_{uv}} 
Hogy a téridő valóban görbüljön; az ebből eredő hatások a gravitáció hatásai.
Kapcsolódó oldalak
- Téridő
- Speciális relativitáselmélet
- Általános relativitáselmélet
| Hatósági ellenőrzés |
|
Kérdések és válaszok
K: Mi az a Minkowski téridő?
V: A Minkowski-téridő egy Hermann Minkowski által létrehozott négydimenziós sokaság. Három térdimenziója (x, y, z) és egy idődimenziója van.
K: Mi a Minkowski-téridő metrikus szignatúrája?
V: A Minkowski-téridő metrikus szignatúrája (-+++).
K: Hogyan ír le a Minkowski-téridő egy sík felületet?
V: Ha nincs tömeg, a Minkowski-téridő sík felületet ír le.
K: A Minkowski-téridő vonatkozik az általános relativitáselméletre?
V: Nem, a Minkowski-téridő csak a speciális relativitáselméletben érvényes. Az általános relativitáselmélet a görbült téridő fogalmát használja a gravitáció és a gyorsított mozgás hatásainak leírására.
K: Hány dimenziója van a Minkowski-téridőnek?
V: A Minkowsi téridőnek négy dimenziója van - három térdimenzió (x, y, z) és egy idődimenzió.
K: Ki alkotta meg a Minkowsi téridő fogalmát?
V: Hermann Minkowksi alkotta meg a MInkowski-téridő fogalmát.
Keres