Lineáris regresszió
A lineáris regresszió egy függő változó és egy vagy több magyarázó változó közötti kapcsolat magyarázatára szolgál egy egyenes segítségével. Ez a regresszióelemzés egy speciális esete.
A lineáris regresszió volt az első olyan regresszióelemzési típus, amelyet szigorúan tanulmányoztak. Ennek oka, hogy az ismeretlen paramétereiktől lineárisan függő modelleket könnyebb illeszteni, mint a paramétereikhez nem lineárisan kapcsolódó modelleket. Ráadásul az így kapott becslők statisztikai tulajdonságai is könnyebben meghatározhatók.
A lineáris regressziónak számos gyakorlati alkalmazása van. A legtöbb alkalmazás a következő két nagy kategória egyikébe sorolható:
- A lineáris regresszió arra használható, hogy előrejelző modellt illesszünk a megfigyelt értékek (adatok) halmazához. Ez akkor hasznos, ha a cél előrejelzés, vagy előrejelzés, vagy csökkentés. Egy ilyen modell kidolgozása után, ha ezután X egy további értékét adjuk meg, a hozzá tartozó y érték nélkül, az illesztett modell felhasználható az y értékének előrejelzésére.
- Adott egy y változó és számos olyan X1, ..., Xp változó, amely kapcsolatban állhat y-val, a lineáris regresszióanalízis alkalmazható az y és az Xj közötti kapcsolat erősségének számszerűsítésére, annak felmérésére, hogy mely Xj-nek nincs kapcsolata y-val, és annak azonosítására, hogy az Xj-ek mely részhalmazai tartalmaznak redundáns információt y-ról.
A lineáris regressziós modellek arra törekednek, hogy az egyenes és az adatpontok (pl. a reziduumok) közötti függőleges távolság a lehető legkisebb legyen. Ezt nevezik "a vonal adatokhoz való illesztésének". A lineáris regressziós modellek gyakran a maradékok négyzeteinek összegét próbálják minimalizálni (legkisebb négyzetek), de az illesztésnek más módjai is léteznek. Ezek közé tartozik az "illeszkedés hiányának" minimalizálása valamilyen más normában (mint a legkisebb abszolút eltérések regressziója esetén), vagy a legkisebb négyzetek veszteségfüggvényének büntetett változatának minimalizálása, mint a ridge-regresszióban. A legkisebb négyzetek megközelítése olyan modellek illesztésére is használható, amelyek nem lineárisak. A fentiek szerint a "legkisebb négyzetek" és a "lineáris modell" kifejezések szorosan kapcsolódnak egymáshoz, de nem szinonimák.
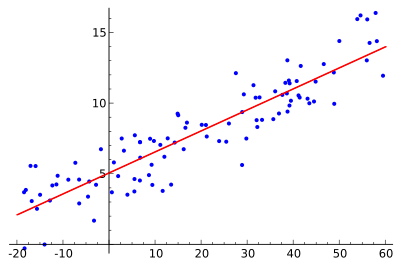
Az ötlet a piros görbe megtalálása, a kék pontok a tényleges minták. A lineáris regresszióval az összes pont egyetlen egyenes vonallal összekapcsolható. Ez a példa egyszerű lineáris regressziót használ, ahol a piros vonal és az egyes mintapontok közötti távolság négyzetét minimalizáljuk.
Használat
Közgazdaságtan
A lineáris regresszió a közgazdaságtan fő elemzési eszköze. Ezt használják például a fogyasztási kiadások, a befektetett beruházási kiadások, a készletberuházások, az ország exportjának vásárlása, az importra fordított kiadások, a likvid eszközök iránti kereslet, a munkaerő-kereslet és a munkaerő-kínálat megbecsülésére.
Kérdések és válaszok
K: Mi az a lineáris regresszió?
V: A lineáris regresszió egy módja annak, hogy a matematika segítségével megvizsgáljuk, hogyan változik valami, amikor más dolgok változnak. Egy függő változót és egy vagy több magyarázó változót használ egy egyenes vonal, az úgynevezett "regressziós egyenes" létrehozásához.
K: Milyen előnyei vannak a lineáris regressziónak?
V: Az ismeretlen paramétereiktől lineárisan függő modelleket könnyebb illeszteni, mint a paramétereikhez nem lineárisan kapcsolódó modelleket. Ezenkívül a kapott becslők statisztikai tulajdonságai könnyebben meghatározhatók.
K: Milyen gyakorlati felhasználási módjai vannak a lineáris regressziónak?
V: A lineáris regresszió arra használható, hogy előrejelző modellt illesszünk a megfigyelt értékekhez (adatokhoz), hogy előrejelzéseket, előrejelzéseket vagy csökkentéseket készítsünk. Használható továbbá a változók közötti kapcsolatok erősségének számszerűsítésére és olyan adatrészletek azonosítására, amelyek egy másik változóra vonatkozó redundáns információt tartalmaznak.
K: Hogyan próbálják a lineáris regressziós modellek minimalizálni a hibákat?
V: A lineáris regressziós modellek arra törekednek, hogy az egyenes és az adatpontok közötti függőleges távolság (a reziduumok) a lehető legkisebb legyen. Ezt vagy a maradékok négyzetösszegének minimalizálásával (legkisebb négyzetek), az illeszkedés hiányának valamilyen más normában való minimalizálásával (legkisebb abszolút eltérések), vagy a legkisebb négyzetek veszteségfüggvényének büntetett változatának minimalizálásával (gerincregresszió) érik el.
Kérdés: Lehetséges, hogy a lineáris regressziós modellek ne a legkisebb négyzeteken alapuljanak?
V: Igen, lehetséges, hogy a lineáris regressziós modellek ne a legkisebb négyzeteken alapuljanak, hanem olyan módszereket használjanak, mint például az illeszkedés hiányának minimalizálása valamilyen más normában (legkisebb abszolút eltérések) vagy a legkisebb négyzetek veszteségfüggvényének büntetett változatának minimalizálása (ridge-regresszió).
K: A "lineáris modell" és a "legkisebb négyzetek" szinonimák?
V: Nem, ezek nem szinonimák. Bár szorosan kapcsolódnak egymáshoz, a "lineáris modell" kifejezetten egy egyenes vonal használatára utal, míg a "legkisebb négyzetek" kifejezetten arra utal, hogy a hibák minimalizálására törekszik azáltal, hogy biztosítja, hogy az egyenes és az adatpontok között minimális legyen a függőleges távolság.
