Görbeillesztés (matematika)
A görbeillesztés egy olyan matematikai függvény megalkotása, amely a legjobban illeszkedik egy adatponthalmazhoz.
A görbeillesztés magában foglalhat interpolációt vagy simítást. Az interpoláció használata pontos illeszkedést igényel az adatokhoz. A simítással egy "sima" függvényt állítunk elő, amely megközelítőleg illeszkedik az adatokhoz. Kapcsolódó téma a regresszióelemzés, amely inkább a statisztikai következtetés kérdéseire összpontosít, például arra, hogy mennyi bizonytalanság van jelen egy olyan görbében, amelyet véletlen hibákkal megfigyelt adatokra illesztünk.
Az illesztett görbék felhasználhatók az adatok vizualizációjának segítésére, egy függvény értékeinek kitalálására, ha nem állnak rendelkezésre adatok, valamint két vagy több változó közötti kapcsolatok összegzésére. Az extrapoláció egy illesztett görbe használatára utal, amely túlmutat a megfigyelt adatok tartományán. Ez bizonyos fokú bizonytalansággal jár, mivel éppúgy tükrözheti a görbe megalkotásához használt módszert, mint a megfigyelt adatokat.
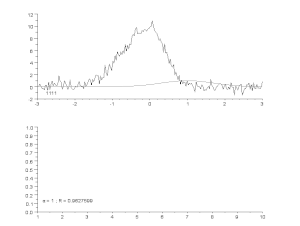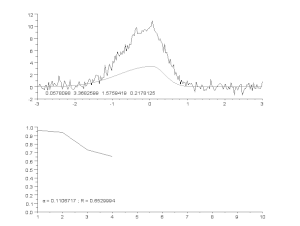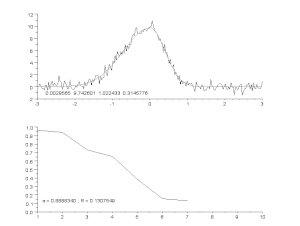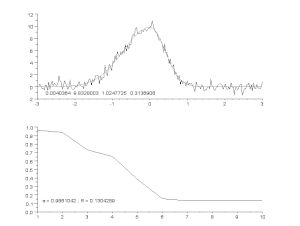
Zajos görbe illesztése aszimmetrikus csúcsmodellel, iteratív eljárással (Gauss-Newton algoritmus változó α csillapítási tényezővel). Fent: nyers adatok és modell. Alul: a hibák négyzeteinek normalizált összegének alakulása.
Kérdések és válaszok
K: Mi az a görbeillesztés?
V: A görbeillesztés egy olyan matematikai függvény létrehozásának folyamata, amely a legjobban illeszkedik egy adatponthalmazhoz.
K: Mi a görbeillesztés két típusa?
V: A görbeillesztés két típusa az interpoláció és a simítás.
K: Mi az interpoláció?
V: Az interpoláció a görbeillesztés olyan típusa, amely az adatok pontos illesztését igényli.
K: Mi az a simítás?
V: A simítás a görbeillesztés olyan típusa, amely egy "sima" függvényt állít elő, amely megközelítőleg illeszkedik az adatokhoz.
K: Mi a regresszióelemzés?
V: A regresszióelemzés egy kapcsolódó téma, amely a statisztikai következtetés kérdéseire összpontosít, például arra, hogy mennyi bizonytalanság van jelen egy olyan görbében, amelyet véletlen hibával megfigyelt adatokra illesztünk.
K: Milyen felhasználási módjai vannak az illesztett görbéknek?
V: Az illesztett görbék segíthetnek az adatok vizualizálásában, egy függvény értékeinek megtippelésében, ahol nem állnak rendelkezésre adatok, és két vagy több változó közötti kapcsolatok összegzésében.
K: Mi az extrapoláció?
V: Az extrapoláció egy illesztett görbe használata a megfigyelt adatok tartományán túl. Ez azonban bizonyos fokú bizonytalansággal jár, mivel a görbe megalkotásához használt módszert éppúgy tükrözheti, mint a megfigyelt adatokat.
