Aranymetszés
Egy a szám és egy másik kisebb b szám esetén a két szám arányát úgy találjuk meg, hogy elosztjuk őket. Az arányuk a/b. Egy másik arányt úgy találunk, hogy a két számot összeadjuk a+b-vel, és ezt elosztjuk a nagyobb a számmal. Az új arány (a+b)/a. Ha ez a két arány megegyezik, akkor ezt a számot aranymetszésnek nevezzük. A φ görög betű \displaystyle \varphi} 
(phi) általában az aranymetszés neveként használják.
Például, ha b = 1 és a/b = φ {\displaystyle \varphi } , akkor a = φ {\displaystyle \varphi } . A második arány (a+b)/a ekkor ( φ + 1 ) / φ {\displaystyle (\varphi +1)/\varphi } 
. Mivel ez a két arány egyenlő, ez igaz:
φ = φ + 1 φ {\displaystyle \varphi ={\frac {\varphi +1}{\varphi }}}
Ezt a számot a következőképpen lehet leírni
φ = 1 + 5 2 {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}}
Az 5 {\displaystyle {\sqrt {5}}}
olyan, mint bármely szám, amely önmagával megszorozva 5-öt ad (vagy amely számot megszoroz): 5 × 5 = 5 {\displaystyle {\sqrt {5}}\times {\sqrt {5}}=5}
.
Az aranymetszés egy irracionális szám. Ha valaki megpróbálja leírni, soha nem fog megállni, és soha nem fog mintát alkotni, hanem így kezdődik: 1,6180339887... Fontos dolog ezzel a számmal kapcsolatban, hogy az ember kivonhat belőle 1-et, vagy oszthat vele 1-et. Akárhogy is, a szám akkor is tovább fog menni, és soha nem fog megállni.
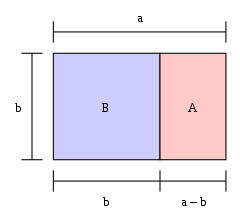
Arany téglalap
Ha egy téglalap hossza osztva a szélességével egyenlő az aranymetszéssel, akkor a téglalap "aranytéglalap". Ha egy arany téglalap egyik végéből levágunk egy négyzetet, akkor a másik vége egy új arany téglalap lesz. A képen a nagy téglalap (kék és rózsaszín együtt) egy arany téglalap, mert a / b = φ {\displaystyle a/b=\varphi } 
. A kék rész (B) egy négyzet. A rózsaszín rész önmagában (A) egy másik arany téglalap, mert b / ( a - b ) = φ {\displaystyle b/(a-b)=\varphi } 
. A nagy téglalap és a rózsaszín téglalap alakja megegyezik, de a rózsaszín téglalap kisebb és elfordított.
A nagy téglalap BA egy arany téglalap, azaz a b:a arány 1: φ {\displaystyle \varphi } . Bármelyik ilyen téglalap esetében, és csak az ilyen arányú téglalapok esetében, ha eltávolítjuk a B négyzetet, akkor az, ami megmarad, A, egy másik arany téglalap; vagyis ugyanazokkal az arányokkal, mint az eredeti téglalap.
Fibonacci-számok
A Fibonacci-számok számok listája. Az ember a lista következő számát úgy találja meg, ha az utolsó két számot összeadja. Ha valaki elosztja a listán szereplő számot az előtte lévővel, akkor ez az arány egyre közelebb kerül az aranymetszéshez.
| Fibonacci-szám | osztva az előzővel | arány |
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2.0000 |
| 3 | 3/2 | = 1.5000 |
| 5 | 5/3 | = 1.6667 |
| 8 | 8/5 | = 1.6000 |
| 13 | 13/8 | = 1.6250 |
| 21 | 21/13 | = 1.6154... |
| 34 | 34/21 | = 1.6190... |
| 55 | 55/34 | = 1.6177... |
| 89 | 89/55 | = 1.6182... |
| ... | ... | ... |
| φ \displaystyle \varphi } | = 1.6180... |
Aranyarány a természetben
A természetben az aranymetszést gyakran használják a levelek vagy virágok elrendezésénél. Ezek a körülbelül 137,5 fokos aranyszöget használják. Az ebben a szögben elrendezett levelek vagy virágok a legjobban kihasználják a napfényt.
Az aranyszög használata optimálisan kihasználja a napfényt. Ez egy nézet a tetejéről.
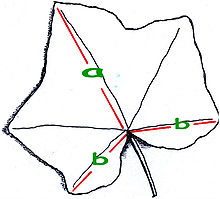
A közönséges borostyán levele, amely az aranymetszést mutatja
Kérdések és válaszok
K: Mi két szám aránya?
V: Két szám arányát úgy találjuk meg, hogy elosztjuk őket, tehát az arány a/b lenne.
K: Hogyan lehet egy másik arányt megtalálni?
V: Egy másik arányt úgy találhatunk, hogy a két számot összeadjuk, majd ezt az összeget elosztjuk a nagyobb számmal, az a-val. Ez az új arány (a+b)/a lenne.
K: Hogyan nevezzük azt, amikor ez a két arány egyenlő egymással?
V: Ha ez a két arány egyenlő egymással, akkor azt aranymetszésnek nevezzük. Általában görög betűvel צ vagy phi betűvel ábrázolják.
K: Ha b = 1 és a/b = צ , mit jelent ez az a-ra nézve?
V: Ha b = 1 és a/b = צ , akkor ez azt jelenti, hogy a = צ is.
K: Hogyan lehet ezt a számot leírni?
V: Ezt a számot így lehet leírni: צ = 1 + 5 / 2 = 1,618...
K: Mit jelent, ha kivonunk belőle 1-et vagy elosztjuk 1-gyel?
V: Ha kivonsz belőle 1-et, vagy osztasz vele 1-et, ugyanazt a számot kapod vissza - vagyis mindkettő megegyezik az aranymetszéssel.
K: Az aranymetszés irracionális szám?
V: Igen, az aranymetszés irracionális szám, ami azt jelenti, hogy ha valaki megpróbálja kiírni, soha nem lesz vége, és nem lesz minta - csak valami olyasmivel kezdődik, hogy "1,6180339887...".
