Fraktál – definíció, önhasonlóság, Mandelbrot és alkalmazások

Fraktál – definíció, önhasonlóság, Mandelbrot és alkalmazások: Ismerd meg a fraktálok matematikáját, vizuális szépségét és gyakorlati felhasználásait.

Szerző: Leandro Alegsa

18-02-2026 20:15

A fraktál olyan mintázat, amely képként nézve olyan képet eredményez, amely nagyítva is ugyanazt a képet adja: a teljesből kivett részek a kiinduló forma kisebb, gyakran önmagukhoz hasonló változatai. Olyan részekre vágható, amelyek a kiindulási kép kisebb változatának tűnnek. A fraktál szót Benoît Mandelbrot alkotta meg 1975-ben a latin fractus szóból, amely "töröttet" vagy "töredezettet" jelent. Egy egyszerű példa erre egy fa, amely kisebb ágakra ágazik, azok pedig kisebb ágakra, és így tovább. A fraktálok nemcsak szépek, hanem számos gyakorlati alkalmazásuk is van.

Önhasonlóság

Az önhasonlóság a fraktálok egyik központi tulajdonsága. Különbséget szokás tenni:

Precis önhasonlóság: a struktúra pontosan ismétlődik különböző méretskálákon (pl. a Koch-görbe, Cantor-halmaz).
Statisztikai önhasonlóság: a szerkezet hasonló jellegű különböző nagyítási szinteken, de nem feltétlenül pontosan ismétlődik — ez jellemző a természetes fraktálokra (pl. partvonalak, felhők).

Fraktál dimenzió

A fraktálok megkülönböztető jellemzője a fraktál dimenzió, amely a hagyományos topológiai dimenziónál finomabb mérőszám és a mintázat "tömöttségét", részletgazdagságát jellemzi különböző méretskálákon. Egyszerű önhasonló esetben a dimenzió kiszámítható a következő képlettel:

D = log(N) / log(1/r), ahol N a darabszám, r pedig a méretarány (azaz minden darab az eredeti r-szorosa).

Példák:

Koch-görbe: N = 4, r = 1/3 → D = log 4 / log 3 ≈ 1,2619.
Cantor-halmaz: N = 2, r = 1/3 → D = log 2 / log 3 ≈ 0,6309.

A fraktál dimenzió gyakran nem egész számú érték, és azt mutatja meg, hogy a halmaz hogyan foglalja el a teret különböző skálákon.

Mandelbrot és kapcsolódó halmazok

Benoît Mandelbrot munkássága tette közismertté a fraktálok fogalmát. A legismertebb fraktálok közé tartozik a Mandelbrot-halmaz, amely egy komplex számon végzett iteráció eredményeiből álló, finom részletekben gazdag, jellegzetes "bimbós" alakzat. A Mandelbrot-halmazhoz szorosan kapcsolódnak a Julia-halmazok, amelyek az egyes komplex paraméterekhez tartozó iteratív rendszerek stabilitási halmazai.

Ezeknél az ún. escape-time algoritmus alkalmazásával határozzuk meg, hogy egy pont pályája végtelen felé szökik-e vagy sem — a határvonalak és a végtelen részletek hozzák létre a fraktál jellegzetességeket.

Fraktálok előállítása

Fraktálok többféle módon hozhatók létre:

Iterált függvényrendszerek (IFS): affinis transzformációk kombinációjával, gyakran nagyon hatékonyak a geometriai, önhasonló fraktálok előállítására.
L-rendszerek: formális grammatika alapú szabályrendszerek, melyek növényi morfológiát és önhasonlóságot modelleznek.
Escape-time algoritmusok: komplex iterációk (pl. Mandelbrot, Julia), ahol pontokat színeznek az iterációs viselkedés alapján.
Random/fraktál zajok: pl. frakcionális Brown-mozgás, melyek természetes, rendezetlen mintázatokat reprodukálnak (felhők, terepmodellek).

Természet és alkalmazások

Fraktálminták sok helyen megjelennek a természetben és a műszaki megoldásokban:

Természet: fákról ágak, vérerek és tüdő légutak elágazódása, partvonalak, hókristályok, hegyvonulatok, felhők.
Számítástechnika és grafika: terepgenerálás, textúrák, képalkotás és művészi vizualizációk.
Mérnöki alkalmazások: fraktál antennák (többsávú, kompakt kialakítás), jelfeldolgozás, tömörítési eljárások (fraktál alapú kép/tömörítés elmélete).
Természettudományok és orvostudomány: érrendszer, tüdő anatómia elemzése, tumorok morfológiája, földtani törésrendszerek modellezése.
Pénzügy és adatmodellezés: komplex idősorok részleteinek elemzése, skálafüggetlen tulajdonságok vizsgálata (multifraktál elemzések).

Jellemző tulajdonságok

Skálainvariancia: a szerkezet hasonló marad eltérő nagyítási szinteken.
Önreferenciális/iteratív felépítés: sok fraktál egyszerű szabályok ismétlésével jön létre.
Végtelen részlet: elméletileg végtelen nagyításnál is új részletek jelennek meg (a numerikus reprezentáció korlátokkal dolgozik).
Nem egész dimenzió: gyakran fraktál dimenziójuk törtszám, ami a komplexitást jellemzi.

Rövid történeti megjegyzés

Bár önhasonló mintázatokról és iteratív görbékről a 19. században is írtak (pl. Cantor, Koch, Peano), a fraktálfogalom rendszerezett elnevezését és népszerűsítését Benoît Mandelbrot végezte el a 20. század második felében. Munkái segítettek felismerni, hogy a természet számos összetett szerkezete hatékonyabban érthető meg fraktál-elmélettel, mint hagyományos euklideszi geometriával.

Hol kezdjem, ha többet szeretnék?

Számos könyv, oktatóanyag és szoftver létezik fraktálok tanulmányozásához. Kezdőknek ajánlott egyszerű példákkal (Koch-görbe, Cantor-halmaz, Sierpiński-háromszög) kísérletezni, majd áttérni IFS-re, L-rendszerekre vagy Mandelbrot/Julia vizualizációkra. A kísérletezéshez elérhetők online generátorok és nyílt forráskódú programok is.

Egy Sierpinski-háromszög, 7 iteráció után.

A Mandelbrot-halmaz a fraktálok híres példája.

Példák

A fraktáloknak sokféle típusa létezik, és nagyon sokféleképpen készülnek. Ilyen például a Sierpinski-háromszög, ahol a nagy háromszög belsejében végtelen számú kis háromszög van. Egy másik példa a Mandelbrot-halmaz, amely Benoît Mandelbrot-ról kapta a nevét. A Sierpinksi-háromszög mintázatok segítségével épül fel, a Mandelbrot-halmaz viszont egy egyenleten alapul.

A természetben is számos természetes példát találunk a fraktálokra, beleértve a fákat, hópelyheket, néhány zöldséget és a partvonalakat.

A Koch-görbe

A Koch-görbe a fraktál egyszerű példája. Először is, kezdjük egy egyenes vonal egy részével - amit egyenes vonalszakasznak nevezünk. Vágjuk az egyenest 3 azonos méretű darabra. Szabadulj meg e darabok közepétől, és tedd be egy olyan háromszög felső részét, amelynek oldalai ugyanolyan hosszúak, mint a kivágandó darab. Most már 4 olyan egyenes szegmensünk van, amelyek a végeiknél összeérnek. Most már mind a 4 darabon megtehetjük azt, amit az imént az első szegmenssel tettünk. Most ugyanezt újra és újra megtehetjük az összes darabkával, amivel a végén rendelkezünk. Most ezt örökké csináljuk, és nézzük meg, hogy mi lesz a végeredmény.

A Koch-görbe hossza végtelen, a Koch-görbe területe pedig nulla. Ez elég furcsa. Egy (1 dimenziójú) vonalszakasz hossza lehet 1, de területe 0. Egy 1 hosszúságú és 1 szélességű (2 dimenziójú) négyzet területe 1, hossza pedig végtelen.

Hasonlósági dimenzió

Tehát a Koch-görbe nagyobbnak tűnik, mint valami 1 dimenziós, és kisebbnek, mint valami 2 dimenziós. A hasonlósági dimenzió lényege, hogy olyan dimenziót adjon, amely a fraktálok esetében jobb képet ad a hosszról vagy a területről. Tehát egy Koch-görbe esetében 1 és 2 közötti dimenziót szeretnénk.

A Koch-görbe négy darabra vágható, amelyek mindegyike az eredeti méretének 1 3 {\displaystyle {\frac {\frac {1}{3}}} ${\frac {1}{3}}$ része. A fraktál N {\displaystyle N} $N$ darabokra vágható darabjainak számát, a méretkülönbséget pedig B {\displaystyle B} $B$ -nek nevezzük. Ezeket beillesztjük az egyenletbe:

log N - log B {\displaystyle {\frac {\log N}{-\log B}}} ${\frac {\log N}{-\log B}}$

Ahol log {\displaystyle \log } $\log$ egy szám logaritmusa. Ez a szám a fraktál Hausdorff-dimenziója. A Koch-görbén ez log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619... } ${\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619...$ ahogyan szerettük volna.

A Koch-görbe az egyik legegyszerűbb fraktál alakzat, így a dimenziója könnyen kiszámítható. A hasonlósági dimenziója és a Hausdorff-dimenziója megegyezik. Ez nem igaz a bonyolultabb fraktálokra.

Koch hópehely

A Koch-hópehely (vagy Koch-csillag) ugyanaz, mint a Koch-görbe, kivéve, hogy egy egyenes szakasz helyett egy egyenlő oldalú háromszöggel kezdődik.

Hogyan készítsük el a Koch-görbét

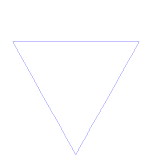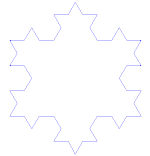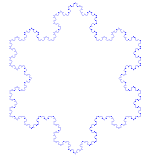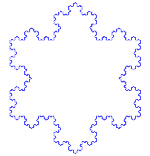
Használja a

A fraktáloknak számos alkalmazási területe van, például a biológiában (tüdő, vesék, szívritmus-változás stb...), a földrengésekben, a pénzügyekben, ahol az úgynevezett nehézfarkú eloszlásokhoz kapcsolódik, és a fizikában. Ez azt jelzi, hogy a fraktálokat tanulmányozni kell, hogy megértsük, miért olyan gyakoriak a fraktálok a természetben.

Egyes fraktálok csak művészi okokból léteznek, mások viszont nagyon hasznosak. A fraktálok nagyon hatékony formák a rádióantennákhoz, és a számítógépes chipekben is használják őket, hogy hatékonyan összekapcsolják az összes alkatrészt. A partvonalakat is fraktálként lehet elképzelni.

Kérdések és válaszok

K: Mi az a fraktál?

V: A fraktál minden olyan minta, amely képként nézve olyan képet eredményez, amely nagyításkor is ugyanazt a képet adja.

K: Kinek tulajdonítják a "fraktál" kifejezés megalkotását?

V: Benoît Mandelbrotnak tulajdonítják a "fraktál" kifejezés 1975-ös megalkotását.

K: Mi az etimológiája a "fraktál" szónak?

V: A "fraktál" szó a latin "fractus" szóból származik, amely "töröttet" vagy "töredezettet" jelent.

K: A fraktálok darabokra vághatók?

V: Igen, a fraktálok részekre vághatók, amelyek úgy néznek ki, mint a kiindulási kép kisebb változatai.

K: Tudna példát mondani egy fraktálra?

V: A fraktál egyszerű példája egy fa, amely kisebb ágakra ágazik, azok pedig kisebb ágakra, és így tovább.

K: Milyen gyakorlati alkalmazásai vannak a fraktáloknak?

V: A fraktáloknak számos gyakorlati alkalmazása van, például a számítógépes grafikában, az orvostudományban, a fizikában és a pénzügyekben.

K: Miért fontosak a fraktálok?

V: A fraktálok azért fontosak, mert segíthetnek megérteni az összetett természeti jelenségeket, és pontosabb modelleket és szimulációkat hozhatnak létre.

Keres