Dimenzió
A dimenziók a világunk meglátásának, mérésének és megtapasztalásának módját jelentik. A fel és le, jobbra-balra, hátra-előre, meleg és hideg, milyen nehéz és milyen hosszú, valamint a matematika és a fizika fejlettebb fogalmainak használatával. A dimenzió meghatározásának egyik módja, hogy megnézzük a szabadságfokokat, vagy azt, hogy egy tárgy hogyan mozoghat egy adott térben. Különböző fogalmak vagy módok vannak, ahol a dimenzió kifejezést használják, és különböző definíciók is léteznek. Nincs olyan definíció, amely minden fogalomnak megfelelne.
Egy vektortérben (a vektor egy nyitott végű vonal) a dimenzió egyenlő a vektorok vagy vonalak kardinalitásával vagy irányainak számával. Ugyancsak megegyezik az adott tér legnagyobb egyenesirányú csoportjának számával. A mindennapi életben használt "normális" tárgyakat három dimenzióval határozzák meg, amelyeket általában hosszúságnak, szélességnek és mélységnek neveznek. A matematikusok ezt a fogalmat euklideszi térnek nevezik.
A méretek a pozíció mérésére is használhatók. A kiindulási helytől mért távolságot a hossz, szélesség és magasság irányában lehet mérni. Ezek a távolságok a pozíció mértékegységei.
Néha egy negyedik (4D) dimenziót, az időt is használják, hogy megmutassák egy esemény helyét az időben és a térben.
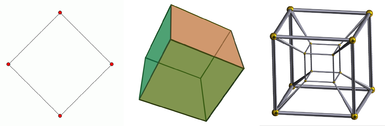
Balról jobbra: a négyzet, a kocka és a tesserakt. A négyzet egy 2 dimenziós tárgy, a kocka egy 3 dimenziós tárgy, a tesserakt pedig egy 4 dimenziós tárgy. Az 1 dimenziós tárgy csak egy vonal. A kocka vetülete adott, mivel kétdimenziós képernyőn nézzük. Ugyanez vonatkozik a tesseraktusra is, amely ráadásul háromdimenziós térben is csak vetületként jeleníthető meg.

Az első négy térbeli dimenzió diagramja.
Egyéb méretek
A modern tudományban az emberek más dimenziókat használnak. Az olyan dimenziók, mint a hőmérséklet és a súly, arra használhatók, hogy megmutassák valaminek a helyzetét kevésbé egyszerű terekben. A tudósok ezeket a dimenziókat dimenzióelemzéssel tanulmányozzák.
A matematikusok is használják a dimenziókat. A matematikában a dimenziók általánosabbak. A matematikai dimenziók nem feltétlenül mérik a világ dolgait. A matematikában a dimenziókkal való számolás szabályai eltérhetnek a szokásos számtani szabályoktól.
Dimenziók és vektorok
A vektorokat távolságok és irányok ábrázolására használják. A vektorokat gyakran használják a mérnöki és természettudományokban, és néha a matematikában is.
A vektor számok listája. Minden dimenzióhoz egy szám tartozik. A vektorokra aritmetikai szabályok vonatkoznak.
Például, ha Jane tudni szeretné Sally helyzetét, Sally adhat Jane-nek egy vektort, amely megmutatja a helyzetet. Ha Jane és Sally a világban vannak, akkor három dimenzió van. Ezért Sally egy három számból álló listát ad Jane-nek, hogy megmutassa a helyzetét. A három szám a vektorban, amelyet Sally Jane-nek ad, a következő lehet:
- Sally távolsága Jane-től északra
- Sally távolsága Jane-től keletre
- Sally magassága Jane felett
Kérdések és válaszok
Q: Mi az a dimenzió?
A: A dimenzió a világ mérésének, meglátásának és megtapasztalásának egy módja, olyan fogalmak segítségével, mint a fent és lent, jobbról balra, hátulról előre, forró és hideg, milyen nehéz és milyen hosszú. Úgy is meghatározható, mint a szabadságfokok vagy az a mód, ahogyan egy tárgy mozoghat egy adott térben.
K: Hogyan definiálják a matematikusok az euklideszi teret?
V: A matematikusok az euklideszi teret három dimenzióval határozzák meg, amelyeket általában hosszúságnak, szélességnek és mélységnek neveznek.
K: Mennyi a vektorok száma egy vektortérben?
V: A vektorok száma egy vektortérben megegyezik az alaphalmaz kardinalitásával (vagy a vektorok számával).
K: Hány dimenziót használunk a pozíció mérésére?
V: A pozíció mérésére három dimenziót (hossz, szélesség és magasság) használunk. Bizonyos esetekben egy negyedik (4D) dimenzió - az idő - is használható egy esemény időbeli és térbeli helyzetének megmutatására.
K: Mit jelent a dim(V)?
V: Dim(V) a V dimenziójára utal, amely megegyezik az alaphalmazának kardinalitásával (vagy a vektorok számával), vagy megegyezik az egyenes irányok számával, amelyekkel rendelkezik.
K: Van olyan definíció, amely minden dimenzióval kapcsolatos fogalmat kielégít?
V: Nem, nincs egyetlen olyan definíció, amely a dimenziókkal kapcsolatos összes fogalomnak megfelelne.
Keres