Stabilitás
A stabilitás számos rendszer tulajdonsága. Azt jelenti, hogy nyugalomban van, nem változik. A mechanikában és a dinamikában egy rendszer akkor stabil (stabil), ha magától nem változtatja meg a mozgását, és ellenáll az irányának vagy helyzetének megváltoztatására irányuló kis erőfeszítéseknek.
Így egy repülő repülőgép dinamikusan stabil, és akkor is ugyanabba az irányba halad, ha a légnyomás (szél) egyenetlenségei megzavarják. Az irányváltoztatáshoz a vezérlőrendszert kell megváltoztatni. Ezzel szemben egy vadászrepülőgép instabil, és azt mindig a pilóta és a számítógép kombinációjának kell irányítania.
A legtöbb nukleáris izotóp instabil, de a világ többnyire stabil izotópokból áll.
Egy hajó esetében a stabilitás azt jelenti, hogy kevésbé valószínű, hogy felborul.
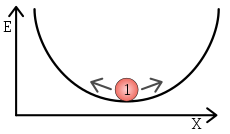
Az elképzelés illusztrációja
