Valószínűségi mező
A valószínűségi tér a tudományos kísérletek leírására használt matematikai modell A valószínűségi tér három részből áll:
- Egy mintatér, amely az összes lehetséges eredményt felsorolja
- Események sorozata. Minden eseményhez nulla vagy több kimenetel társul
- Egy függvény, amely valószínűségeket rendel az egyes eseményekhez.
Az eredmény a modell egyetlen végrehajtásának eredménye. Mivel az egyes kimeneteknek kevés gyakorlati haszna lehet, a kimenetek csoportjainak jellemzésére összetettebb eseményeket használunk. Az összes ilyen esemény gyűjteménye egy σ-algebra F {\displaystyle \scriptstyle {\mathcal {F}}} 
. Végül meg kell adni az egyes események bekövetkezési valószínűségét. Ezt a P valószínűségi mértékfüggvény segítségével tehetjük meg.
Miután a valószínűségi tér kialakult, feltételezzük, hogy a "természet" megteszi a lépését, és kiválaszt egyetlen kimenetet, ω-t, az Ω mintatérből. Az F {\displaystyle \scriptstyle {\mathcal {F}}} összes olyan eseményét, amely tartalmazza a kiválasztott ω kimenetet (emlékezzünk arra, hogy minden esemény az Ω részhalmaza), "bekövetkezettnek" mondjuk. A természet által végzett szelekció úgy történik, hogy ha a kísérletet végtelen sokszor megismételnénk, akkor az egyes események relatív előfordulási gyakorisága egybeesne a P függvény által előírt valószínűségekkel.
Andrej Kolmogorov szovjet matematikus az 1930-as években vezette be a valószínűségi tér fogalmát, a valószínűségszámítás más axiómáival együtt.
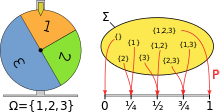
A szerencsekerék modellezése a valószínűségi tér segítségével
Kérdések és válaszok
K: Mi az a valószínűségi tér?
A: A valószínűségi tér egy matematikai modell, amelyet tudományos kísérletek leírására használnak. Három részből áll: egy mintatérből, amely az összes lehetséges kimenetet felsorolja, egy eseményhalmazból, amely nulla vagy több kimenetelt társít, és egy függvényből, amely valószínűségeket rendel az egyes eseményekhez.
K: Miből áll a mintatér?
V: A mintatér az összes lehetséges kimenetelből áll, gyakran Ω {\displaystyle \Omega} formában írva. , és egy kimenetel ω {\displaystyle \omega } .
K: Mi az a kimenetel?
V: A kimenetel a modell egyetlen végrehajtásának eredménye.
K: Mire használják az eseményeket a valószínűségi terekben?
V: Az eseményeket a kimenetek csoportjainak jellemzésére használják, mivel az egyes kimeneteknek kevés gyakorlati haszna lehet. Az összes ilyen esemény gyűjteményét σ-algebrának nevezzük, néha F {\displaystyle {\mathcal {F}}} néven írjuk.
K: Hogyan rendelnek valószínűségeket az egyes eseményekhez?
V: A valószínűségeket a P valószínűségi mértékfüggvény segítségével rendeljük az egyes eseményekhez.
K: Ki vezette be a valószínűségi terek fogalmát? V: Andrej Kolmogorov, a szovjet matematikus az 1930-as években a valószínűségi axiómákkal együtt bevezette a valószínűségi terek fogalmát.
