Euler-Bernoulli-Féle gerendaelmélet
Az Euler-Bernoulli-féle gerendaelmélet (más néven mérnöki gerendaelmélet vagy klasszikus gerendaelmélet) egy egyszerű módszer a gerendák hajlításának kiszámítására terhelés hatására. Ez a gerenda kis alakváltozásaira (hogy valami mennyire mozdul el) vonatkozik, a nyírási alakváltozások hatásainak figyelembevétele nélkül. Ezért a Timosenko-féle gerendaelmélet speciális esetének tekinthető. Először 1750 körül vezették be. A 19. század végén az Eiffel-torony és az óriáskerék fejlesztése során vált népszerűvé. Ezt követően számos mérnöki területen alkalmazták, többek között a gépészetben és az építőmérnöki szakmában. Bár más fejlett módszereket is kifejlesztettek, az Euler-Bernoulli-féle gerendaelméletet egyszerűsége miatt még mindig széles körben használják.
Egy rezgő üveggerenda, amely a gerendák elhajlását mutatja, amely az Euler-Bernoulli-féle gerendaelmélet segítségével becsülhető.
Történelem
Leonhard Euler és Daniel Bernoulli állították össze elsőként az elméletet 1750-ben. Abban az időben a tudományt és a mérnöki tudományokat másképp tekintették, mint manapság. Az olyan matematikai elméletekben, mint az Euler-Bernoulli-féle gerendaelmélet, nem bíztak a gyakorlati mérnöki alkalmazásban. A hidakat és az épületeket egészen a 19. század végéig ugyanazokkal a módszerekkel tervezték. Ekkor az Eiffel-torony és az óriáskerék megmutatta az elmélet érvényességét nagyobb léptékben.
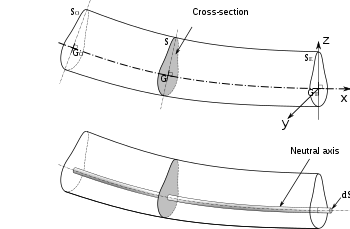
Egy hajlított gerenda keresztmetszetének rajza a semleges tengelyt ábrázolva
Statikus gerendaegyenlet
Az Euler-Bernoulli-egyenlet az alábbiakban látható módon írja le a gerenda alakváltozásának és az alkalmazott terhelésnek a kapcsolatát:
d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}\right)=q\,} 
Ahol w ( x ) {\displaystyle w(x)} a gerendának a z {\displaystyle z}
irányban történő elhajlását írja le
egy bizonyos x {\displaystyle x}
pozícióban. q {\displaystyle q}
egy eloszló terhelés, más szóval egy egységnyi hosszra jutó erő (analóg a nyomással, amely egy területre jutó erő); ez lehet az x {\displaystyle x} , w {\displaystyle w} függvénye. 
vagy más változók függvénye.
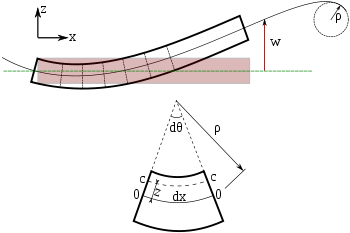
Egy Euler-Bernoulli gerenda hajlítása. A gerenda minden keresztmetszete 90 fokban áll a semleges tengelyhez képest.
Kérdések és válaszok
K: Mi az Euler-Bernoulli-féle sugárelmélet?
V: Az Euler-Bernoulli gerendaelmélet egy egyszerű módszer, amelyet gerendák hajlításának kiszámítására használnak terhelés hatására, a nyírási deformációk hatásainak figyelembevétele nélkül.
K: Mikor vezették be először az Euler-Bernoulli-féle gerendaelméletet?
V: Az Euler-Bernoulli-féle gerendaelméletet 1750 körül vezették be először.
K: Az Euler-Bernoulli-féle gerendaelméletet használták az Eiffel-torony és az óriáskerék kifejlesztésekor?
V: Igen, az Euler-Bernoulli-féle gerendaelmélet az Eiffel-torony és az óriáskerék fejlesztése során vált népszerűvé a 19. század végén.
K: Melyek azok a mérnöki területek, ahol az Euler-Bernoulli gerendaelméletet alkalmazták?
V: Az Euler-Bernoulli-féle gerendaelméletet számos mérnöki területen alkalmazták, többek között a gépészetben és az építőmérnöki tudományokban.
K: Az Euler-Bernoulli-féle gerendaelméletet ma is széles körben alkalmazzák?
V: Igen, az Euler-Bernoulli-féle gerendaelméletet egyszerűsége miatt ma is széles körben használják, annak ellenére, hogy más fejlett módszereket fejlesztettek ki.
K: Milyen típusú gerendahajlásokra alkalmazható az Euler-Bernoulli-féle gerendaelmélet?
V: Az Euler-Bernoulli-féle gerendaelmélet a gerenda kis alakváltozásaira vonatkozik.
K: Az Euler-Bernoulli-féle gerendaelmélet figyelembe veszi a nyírási alakváltozások hatásait?
V: Nem, az Euler-Bernoulli gerendaelmélet nem veszi figyelembe a nyírási deformációk hatásait.
