Holland séma-tétele — definíció és szerepe a genetikus algoritmusokban

Holland séma-tétele: részletes definíció és gyakorlati szerep a genetikus algoritmusokban — hogyan magyarázza a sémák terjedését és befolyásolja az evolúciós keresést.

Szerző: Leandro Alegsa

24-03-2026 00:00

Holland sématétele, amelyet gyakran a genetikus algoritmusok (GA-k) alaptételének is neveznek, egy formális egyenlőtlenség, amely a populáció evolúciós dinamikájának durva szemcsésítéséből származik. A tétel lényege, hogy a rövid, alacsony rendű és átlagon felüli fitneszű sémák (minták) relatív gyakorisága hajlamos növekedni az egymást követő generációkban. A megfogalmazást és az első vizsgálatokat John Holland végezte az 1970-es években; eredetileg sokan úgy vélték, hogy ez magyarázatot ad a genetikai algoritmusok működésére és sikerére. Az elmúlt évtizedekben azonban a tétel értelmezését és jelentőségét számos kritika érte, és publikációk mutatták be, hogy a séma-tétel a Price-egyenlet egy speciális esete, ahol a séma indikátorfüggvénye szolgál makroszkopikus mérőszámként.

Mi az a séma?

A séma egy sablon, amely a lehetséges karakterláncok (egy megadott ábécé és hossz mellett) egy részhalmazát jelöli. A sémák leírására gyakran használnak egy speciális helyőrzőt (például a '*'), amely a „bármi” karaktert jelenti egy pozícióban. Például a bináris ábécé esetén az 1*0**1 séma azokat a hosszú bit-sorozatokat fogja össze, amelyek az első pozícióban 1-et, a harmadik pozícióban 0-t, és az utolsóban 1-et tartalmaznak (a többi pozíció tetszőleges lehet).

A sémákat két fontos mennyiséggal szokás jellemezni:

rend (order, o(H)): a sémában fixált (nem helyőrző) pozíciók száma. (Példánkban o = 3.)
definiáló hossz (defining length, δ(H)): a legelső és legutolsó fix pozíció indexe közötti távolság. (Példánkban ez a távolság a 1. és az utolsó pozíció között mérve.)

A sémák speciális esetei a hengerhalmazoknak; topológiai értelemben így topológiai teret alkotnak, ami elméleti következtetésekhez használható.

A séma-tétel állítása és képlete (röviden)

A klasszikus séma-tétel egy felső közelítés helyett általában egy alsó becslést ad arra, hogyan változik egy séma előfordulásainak száma egy lépésben a szelekció, keresztezés és mutáció hatására. Jelölve m(H,t)-vel a H sémát hordozó egyedek számát a t-edik generációban, a tétel a következő várható értékbeli egyenlőtlenséget adja (egyszerűsített formában, egy-pontos keresztezésre és független bitmutációra):

E[m(H,t+1)] ≥ m(H,t) · (f(H)/f̄) · (1 − p_c · δ(H)/(l−1)) · (1 − p_m)^{o(H)}

Itt:

f(H) a H sémát hordozó egyedek átlagos fitnesze,
f̄ a teljes populáció átlagfitnesze,
p_c a keresztezés valószínűsége,
p_m az egybites mutáció valószínűsége,
l a kromoszómahossz (karakterláncok hossza),
δ(H) és o(H) a fent definiált mennyiségek.

Értelmezés: ha a H sémát tartalmazó egyedek átlagfitnesze nagyobb, mint a populáció átlaga, akkor a szelekció következtében várhatóan több H-t hordozó egyed lesz a következő generációban. Ezt azonban csökkentheti a keresztezés (különösen, ha a defináló hossz nagy) és a mutáció (különösen, ha a rend nagy) — ezért a rövid, alacsony rendű, átlagon felüli fitneszű sémák különösen „sikeresek”.

Gyakorlati szerepe a genetikus algoritmusokban

Értelmező keret: a séma-tétel rávilágít arra, hogy a GA-k hogyan képesek összegyűjteni és kombinálni hasznos részmegoldásokat (ún. building block-ok), különösen ha a reprezentáció és a genetikai operátorok támogatják a rövid, informatív sémák megőrzését.
Tervezési szempontok: a tételből következik, hogy érdemes olyan reprezentációt és keresztezési mechanizmust választani, amelyek nem töri szét túl gyakran a rövid, hasznos sémákat; illetve a mutációs rátát se tegyük feleslegesen magasra.
Diagnosztika és intuíció: a tétel jó szemléltető eszköz arra, hogy miért működnek bizonyos GA-beállítások, de nem mindig ad pontos előrejelzést adott probléma és parametrizáció mellett.

Kritika és korlátok

Bár a séma-tételt gyakran „alaptételnek” nevezték, több fontos korlátozása van:

Formális, nem prediktív: a tétel általában alsó becslést ad, és nem garantálja a gyakorlatbeli teljesítményt különböző problémákon és parametrizációkon.
Egyszerűsítések: a klasszikus képlet feltételez bizonyos keresztezési modell(oka)t (pl. egyszerű egy-pontos keresztezés) és független genetikai hatásokat, ami nem mindig érvényes összetett reprezentációk vagy operátorok esetén.
Price-egyenlet és tautológia: kutatók megmutatták, hogy a séma-tétel matematikailag a Price-egyenlet egy speciális esete, ami azt sugallja, hogy a tétel nem ad új csodát, inkább egy adott aggregált mérőszámra (séma-indikátorra) alkalmazott általános evolúciós identitás.
Konekciós és epistasztikus hatások: ha a problémában erős kölcsönhatások (epiztázis) vannak a gének között, vagy a hasznos részek nem olyan rövidek és könnyen összeilleszthetők, akkor a building-block intuitív sikere csökkenhet.

Mai nézőpont

A séma-tétel fontos történeti és pedagógiai szerepet tölt be a GA-k elméletében: egyszerű, intuitív magyarázatot ad arra, hogyan lehet részmegoldásokat kombinálni. Ugyanakkor a modern kutatás sokkal kifinomultabb eszközöket használ (pl. konkrét probléma-adaptált analízisek, markov-láncok, információelméleti és kombinatorikus megközelítések), és a gyakorlati GA-tervezésnél gyakran empirikus tanulmányokra és finomhangolásra támaszkodnak. A séma-tétel ezért ma elsősorban elméleti iránytű és oktatási eszköz, nem pedig univerzális teljesítménygarancia.

Leírás

Tekintsük a 6 hosszúságú bináris karakterláncokat. Az 1*10*1 séma az összes olyan 6 hosszúságú karakterlánc halmazát írja le, amelynek 1., 3. és 6. pozíciójában 1-es, a 4. pozíciójában pedig 0 van. A * egy joker szimbólum, ami azt jelenti, hogy a 2. és az 5. pozíció 1 vagy 0 értékű is lehet. A séma o ( H ) {\displaystyle o(H)} $o(H)$ sorrendjét a sablonban lévő rögzített pozíciók számaként határozzuk meg, míg a meghatározó hossz δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ az első és az utolsó konkrét pozíció közötti távolságot jelenti. Az 1*10*1 sorrendje 4, a meghatározó hossza pedig 5. Egy séma fitneszértéke a sémának megfelelő összes karakterlánc átlagos fitneszértéke. Egy karakterlánc alkalmassága a kódolt problémamegoldás értékének egy problémaspecifikus kiértékelő függvény által kiszámított mértéke. A genetikus algoritmusok bevált módszereit és genetikai operátorait alkalmazva a séma-tétel kimondja, hogy az átlagon felüli fitneszű rövid, alacsony rendű sémák exponenciálisan növekednek az egymást követő generációkban. Egyenletben kifejezve:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {\displaystyle \operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Itt m ( H , t ) {\displaystyle m(H,t)} $m(H,t)$ a H sémához {\displaystyle H} $H$ tartozó karakterláncok száma a t generációban {\displaystyle t}. $t$ , f ( H ) {\displaystyle f(H)} $f(H)$ a H {\displaystyle H} $H$ séma megfigyelt átlagos fitneszértéke és a t {\displaystyle a_{t}} $a_{t}$ a t {\displaystyle t} $t$ generációban megfigyelt átlagos fitneszértéke. A p {\displaystyle p} $p$ bomlás valószínűsége annak a valószínűsége, hogy a keresztezés vagy a mutáció elpusztítja a H {\displaystyle H} $H$ sémát. Ez a következőképpen fejezhető ki:

p = δ ( H ) l - 1 p c + o ( H ) p m {\displaystyle p={\delta (H) \over l-1}p_{c}+o(H)p_{m}}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

ahol o ( H ) {\displaystyle o(H)} $o(H)$ a séma sorrendje, l {\displaystyle l} $l$ a kód hossza, p m {\displaystyle p_{m}} $p_{m}$ a mutáció valószínűsége és p c {\displaystyle p_{c}} $p_{c}$ a keresztezés valószínűsége. Tehát egy rövidebb definíciós hosszúságú δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ séma kisebb valószínűséggel bomlik meg.
Gyakran félreértik, hogy a sématétel miért egyenlőtlenség és nem egyenlőség. A válasz valójában egyszerű: a tétel elhanyagolja azt a kis, de nem nulla valószínűséget, hogy a H {\displaystyle H} $H$ sémához tartozó karakterlánc "nulláról" jön létre egy olyan karakterlánc mutációjával (vagy két karakterlánc rekombinációjával), amely az előző generációban nem tartozott a H {\displaystyle H} $H$ sémához.

Korlátozás

A sématétel egy végtelen nagy populációt fenntartó genetikai algoritmus feltételezése mellett érvényes, de nem mindig érvényesül a (véges) gyakorlatban: a kezdeti populáció mintavételi hibája miatt a genetikai algoritmusok olyan sémákhoz konvergálhatnak, amelyek nem rendelkeznek szelektív előnnyel. Ez különösen a multimodális optimalizálásban fordul elő, ahol egy függvénynek több csúcsa is lehet: a populáció sodródhat úgy, hogy az egyik csúcsot preferálja, a többit pedig figyelmen kívül hagyja.

A sématétel azért nem tudja megmagyarázni a genetikai algoritmusok erejét, mert minden problémapéldányra érvényes, és nem tud különbséget tenni olyan problémák között, amelyekben a genetikai algoritmusok rosszul teljesítenek, és olyanok között, amelyekben a genetikai algoritmusok jól teljesítenek.

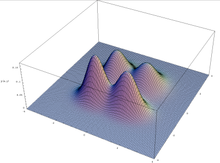
Egy multimodális függvény ábrázolása két változóban.

Kérdések és válaszok

K: Mi a Holland-féle sématétel?

V: Holland sématétele egy genetikai algoritmusokkal kapcsolatos tétel, amely szerint az átlagosnál magasabb fitneszű egyedek nagyobb valószínűséggel érvényesülnek.

K: Ki és mikor javasolta Holland sématételét?

V: John Holland az 1970-es években javasolta a Holland sématételt.

K: Mi az a séma a genetikai algoritmusokkal összefüggésben?

V: A genetikai algoritmusokkal összefüggésben a séma egy olyan sablon, amely azonosítja a karakterláncok egy részhalmazát, amelyek bizonyos karakterlánc-pozíciókban hasonlóságot mutatnak.

K: Hogyan értelmezhető Holland sématétele, amely a genetikai algoritmusok erejének magyarázatának alapjául szolgált?

V: Holland sématételének értelmezése, amelyet a genetikai algoritmusok erejének magyarázatának alapjául használtak, az, hogy az átlagosnál magasabb fitneszű egyedek nagyobb valószínűséggel érvényesülnek.

K: Mit mutatott ki a Holland sématételével kapcsolatos kritika?

V: A Holland sématételének kritikája azt mutatta ki, hogy az a Price-egyenlet egy speciális esete, amelyben a sémaindikátor-függvény a makroszkopikus mérőszám.

K: Mi a hengerhalmazok speciális esete?

V: A sémák a hengerhalmazok speciális esete.

K: Milyen teret alkotnak a sémák?

V: A sémák topológiai teret alkotnak.

Keres