Szögsebesség — definíció, mértékegységek, vektor és forgásirány

Ismerd meg a szögsebesség definícióját, mértékegységeit, vektorát és a forgásirány meghatározását egyszerűen, példákkal és képletekkel.

A fizikában a szögsebesség azt a szögsebességet adja meg, amellyel egy tárgy forog, valamint a forgás irányát.

Matematikai definíció

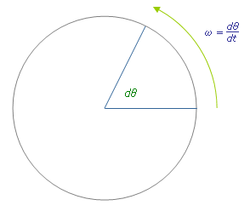
A szögsebesség (gyakran ω vagy Ω jelöléssel) a szög változásának időegységre vetített mértéke. Egydimenziós, síkbeli forgás esetén az idő szerinti differenciális formája:

ω = dθ/dt,

ahol θ a szög (radiánban), t az idő. Ezt az értéket gyakran pillanatnyi szögsebességnek nevezzük; egy adott időintervallumra számított hányados pedig az átlagos szögsebesség.

Mértékegységek és átváltás

A szögsebesség SI-egysége a radián/másodperc (rad/s). A radián dimenziótlan mennyiség, így a szögsebesség dimenziója 1/s. Gyakoribb egyéb mértékegységek és átváltásaik:

• fok/másodperc (°/s) — 1 rad/s = 180/π °/s
• fordulat/perc (RPM) — 1 RPM = 2π/60 rad/s ≈ 0,10472 rad/s
• ciklus/s (Hz) = frekvencia f — ω = 2π f

Tehát kapcsolat a frekvenciával és periódussal: ω = 2π f = 2π / T.

Vektor, irány és jobbkéz-szabály

A szögsebesség vektora a forgás síkjára merőleges irányú, nagysága a forgási sebesség, iránya pedig a forgás orientációját adja meg. A legtöbb fizikában alkalmazott konvenció a jobbkéz-szabály: ha a jobb kéz ujjait a forgás irányába hajlítjuk, akkor a kinyújtott hüvelykujj mutatja a szögsebesség vektorának irányát.

Fontos azonban megjegyezni, hogy a forgás vektoros megközelítése egy pszeudovektor-ral dolgozik (a tényleges forgás nem egy "normál" vektorral mérhető mennyiség), és a véges forgatások nem kommutatívak: két egymást követő, nagy elfordulás nem feltétlen ad ugyanazt az eredményt, mint fordított sorrendben. Azonban a pillanatnyi (infinitézimalis) szögsebességek vektoriálisan összeadhatók.

Kapcsolat a lineáris sebességgel

Ha egy test egy r távolságban lévő pontja forog egy tengely körül, akkor a pont lineáris sebessége és a szögsebesség között a kapcsolat:

v = ω × r,

ahol v a pont sebességvektora, ω a szögsebesség vektora, r pedig a tengelytől mért helyvektor. Egyszerű körmozgás esetén a nagyságok kapcsolata: v = ω r.

Alkalmazások és példák

• Kerék forgása: ha egy kerék 60 RPM-mel forog, akkor ω = 60·2π/60 = 2π rad/s.
• Föld forgása: a Föld szöggyorsulása ~7,2921·10^−5 rad/s (egy teljes fordulat ~24 óra alatt).
• Giroszkópok és precesszió: a forgó testek esetén a forgási impulzus és külső forgatónyomatékok miatt előforduló viselkedés (precesszió) leírásában a szögsebesség alapvető szerepet játszik.

Megjegyzések

• A szögsebesség jelölései: gyakori jelölés ω (kis görög omega), néha nagy Ω is használatos.
• A szögsebesség a mozgásegyenletekben és a dinamika leírásában kulcsfontosságú mennyiség, különösen forgó rendszerek, harmonikus oszcillátorok és mechanikai rendszerek analizálásánál.
• Háromdimenziós mozgásoknál a szögsebességet gyakran mátrix- vagy antiszimmetrikus tenzorként is kezelik, különösen akkor, ha a forgások komponensei változnak és tengelyek kombinálódnak.

Kérdések és válaszok

K: Mi az a szögsebesség?

K: Mi a szögsebesség SI-egysége?

K: A szögsebesség mérhető más mértékegységben is?

K: Milyen kifejezést használnak, amikor a szögsebességet időegységre vetített ciklusokban vagy fordulatszámokban mérik?

K: Milyen szimbólumot szoktak használni a szögsebesség ábrázolására?

K: Milyen irányra merőleges a szögsebesség vektor?

K: A szögsebesség skalár vagy vektormennyiség?

Keresés betűvel