Young–Laplace-egyenlet: definíció, képlet és alkalmazások
Young–Laplace-egyenlet: definíció, képlet és alkalmazások — felületi feszültség, kapilláris nyomáskülönbség és élettani, ipari alkalmazások áttekintése.
A fizikában a Young-Laplace-egyenlet (/ləˈplɑːs/) egy nemlineáris parciális differenciálegyenlet, amely a két statikus folyadék, például víz és levegő közötti határfelületen fellépő kapilláris nyomáskülönbséget írja le. Ez a különbség a felületi feszültség jelenségének köszönhető. A falfeszültség kifejezést csak bizonyos, nagyon vékony falú rendszereknél szokták használni. A Young–Laplace-egyenlet a nyomáskülönbséget a felület görbületi tulajdonságaival hozza összefüggésbe, ezért alapvető a statikus kapilláris felületek és buborékok alakjának vizsgálatában.
Képlet és alapfogalmak
A legegyszerűbb alakban a Young–Laplace-egyenlet így írható fel:
Δp = γ (1/R1 + 1/R2) = 2γH
ahol
- Δp = p_belül − p_kívül a határfelületen átütő nyomáskülönbség,
- γ a felületi feszültség (folyadék–gáz felület esetén),
- R1 és R2 a felület két fő görbületi sugara (principal radii),
- H a felület közép görbülete (mean curvature), amely sok definícióban H = (1/2)(1/R1 + 1/R2).
Gyakori speciális esetek:
- Szigorúan gömb alakú felületnél R1 = R2 = R, így Δp = 2γ/R (például szabad buborékban nagyobb belső nyomás a külsőhöz képest).
Értelemezés és fizikai következmények
A képlet alapján minél kisebb a buborék vagy csepp sugara, annál nagyobb a belső nyomás. Ez magyarázza például azt, hogy a nagyon apró cseppek gyorsabban párolognak: a belső nyomás növeli a gőznyomást. Ha Δp = 0 (például két oldalon azonos nyomás), akkor a felületnek minimális felület jellegű, azaz H = 0 feltételnek megfelelő alakúnak kell lennie (például végtelen sík vagy bizonyos minimalfelületek).
Kapcsolódó egyenletek a gyakorlatban
Ha a gravitációt is figyelembe vesszük, a helyi belső nyomás magasságtól függően változik (hidrosztatikus tag), ezért a felület alakját a Young–Laplace-egyenlet és a hydrostatika együtt határozza meg. Ebből adódik a kapilláris hossz λc = sqrt(γ/(ρ g)), amely megmutatja, hogy milyen méret alatt lesz a felületi feszültség domináns a gravitációval szemben.
Példa kapilláris emelkedésre: egy hengeres kapilláris esetén a folyadék felszíne h magasságig emelkedik, ahol
h = (2 γ cos θ) / (ρ g r),
ahol θ a kontaktuszög, r a kapilláris belső sugara, ρ a sűrűség és g a gravitációs gyorsulás.
Alkalmazások
- Kapillaritás és meniszkusz alakok: a csőben felálló folyadékszintek és a csőfalhoz való nedvesedés vizsgálata.
- Buborékok és cseppek stabilitása, párolgása, és koaleszcenciája (buborékok összeolvadása).
- Felületi jelenségek a mikrofluidikában és nanotechnológiában—kis méretekben a felületi feszültség uralja a viselkedést.
- Élettani alkalmazások: a Laplace-törvény néven ismert alakját használják üreges szervekben (pl. tüdő alveolusai, érrendszeri falak) a transmuralis nyomás, a sugár és a falban fellépő erők kapcsolatának egyszerűsítésére. Ilyenkor gyakori forma: gömb esetén T = p R / 2, henger esetén T = p R (T a falban fellépő körkörös feszültség vagy felületi feszültség jellegű erő egységnyi hosszra).
- Ipari alkalmazások: cseppképződés fúvókáknál, habok és emulziók stabilitása, felületi bevonatok és tisztítószerek hatása.
Korlátozások és kiterjesztések
- A klasszikus Young–Laplace-egyenlet állandó, izotróp felületi feszültsést feltételez. Ha a felületi feszültség térben vagy időben változik (például felületi szennyezők, surfaktánsok jelenléte, Marangoni-effektus), további síkok és tömegáramlások jelennek meg.
- Dinamikus helyzetekben (folyadékmozgás, viszkózus hatások) a képlet statikus változata nem elegendő; ilyenkor a Navier–Stokes-egyenletekkel kell kombinálni a határfeltételeket.
- Rugalmas vagy képlékeny membránoknál a felületi feszültsés mellett az anyag rugalmassága (Helfrich-energia, görbületi energiák) is hozzájárul a nyomáskülönbséghez, így a Young–Laplace alak bővítést igényel.
- Nanoskálán vonallégfeszültség (line tension) és diszkrét molekuláris hatások is szerephez juthatnak, amelyek eltérítik a klasszikus képletet.
Történeti megjegyzések
Az egyenlet Thomas Young nevét viseli, aki 1805-ben megfogalmazta a felületi feszültség minőségi elméletét. Pierre-Simon Laplace egy évvel később elkészítette a matematikai leírást, innen a kettős név. Néha Young–Laplace–Gauss-egyenletként is említik, mert Carl Friedrich Gauss 1830 körül egységesítette a korábbi eredményeket és Bernoulli virtuális munkáját felhasználva vezette le mind a differenciálegyenletet, mind a peremfeltételeket — erről részletesebben is olvashatunk a korai művekben. A cikk bevezetőjében szereplő történeti tényeket érdemes összevetni a korszak irodalmával; a fizikai fogalmak mai formáját ezek a munkák alapozzák meg.
Összefoglalva: a Young–Laplace-egyenlet a felületi feszültség és a görbület kapcsolatát adja meg, és számos természeti és műszaki jelenség alapját képezi — a mikroszkopikus cseppektől a biológiai szervekig.
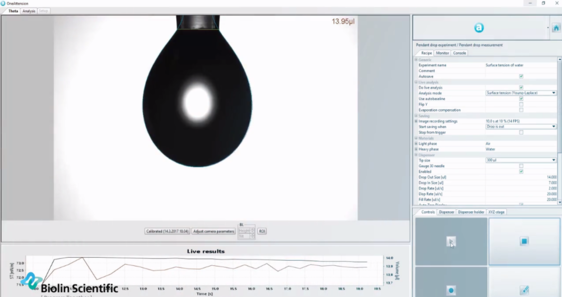
Az optikai tenziométerek a Young-Laplace-egyenletet használják a folyadék felületi feszültségének automatikus meghatározására a függő cseppek alakja alapján.
Kérdések és válaszok
K: Mi az a Young-Laplace-egyenlet?
V: A Young-Laplace-egyenlet egy nemlineáris parciális differenciálegyenlet, amely leírja a kapilláris nyomáskülönbséget két statikus folyadék, például víz és levegő közötti határfelületen.
K: Mihez kapcsolódik?
V: A nyomáskülönbséget a felület vagy fal alakjával hozza összefüggésbe.
K: Ki fejlesztette ki ezt az elméletet?
V: Az elméletet Thomas Young dolgozta ki 1805-ben, és Pierre-Simon Laplace a következő évben fejezte be a matematikai leírását. Később Carl Friedrich Gauss 1830-ban egységesítette.
K: Hogyan használják az élettanban?
V: A fiziológiában Laplace-törvényként ismert, és az üreges szervekben uralkodó nyomás leírására használják.
K: Milyen jelenséget magyaráz meg?
V: A Young-Laplace-egyenlet a felületi feszültség vagy falfeszültség jelenségét magyarázza.
K: A falfeszültség vastag falak esetén is alkalmazható? V: Nem, a falfeszültség csak nagyon vékony falak esetén alkalmazható.
Keres