Bernoulli-elv (definíció): a nyomás és a sebesség kapcsolata
Bernoulli-elv: hogyan és miért csökken a nyomás a növekvő sebességnél — egyszerű magyarázat, képek és példák a folyadékdinamikában.
A Bernoulli-elv a folyadékdinamika egyik alapelve. Eszerint a folyadék sebességének növekedésével csökken a nyomás. Ezt szemlélteti a keskenyedő cső példája: a cső széles részében a folyadék (vagy gáz) statikus nyomása nagyobb, mint a vékony részen, mert az áramlás egyenletességének megőrzéséhez — ha a sűrűség közel állandó marad — a keresztmetszet csökkenésével a sebesség nő (continuity: A1·v1 = A2·v2). Ez a hatás jól látható például Venturi-csőben vagy a fúvókarendszerekben.
Amikor egy erő egy területre hat, azt "nyomásnak" nevezzük. A nagyobb nyomás a folyadékot az alacsonyabb nyomás felé nyomja (gyorsítja). Tehát bármilyen sebességváltozáshoz nyomásváltozásnak kell társulnia — energiaátalakulás történik a folyadékrészecskék mozgási és a nyomásból származó energiája között. Bernoulli hangsúlyozta, hogy ez a kapcsolat egy adott áramvonal mentén érvényes: az egyetlen útvonalon belüli sebesség- és nyomásváltozásokra vonatkozik, és nem közvetlenül hasonlít össze két különböző áramvonalat, amelyek eltérő feltételek mellett haladnak.
A Bernoulli-elv teljes, gyakran használt alakja az energia megmaradását írja le egységnyi térfogat vagy egységnyi tömeg szemszögéből. Az egyszerűsített egyenlet (incompressible, súrlódásmentes, stacioner áramlás esetén) formálisan:
p + ½ρv² + ρgh = állandó
ahol p a statikus nyomás, ρ a közeg sűrűsége, v a sebesség, g a gravitációs gyorsulás és h a magasság (potenciális energia szerinti helyzet). Ebből látható, hogy a nyomás, a mozgási energia (dinamikus nyomás) és a potenciális energia összege állandó az áramvonal mentén, ha a feltételek teljesülnek. (Bernoulli nem veszi figyelembe a viszkozitást vagy a tömöríthetőséget, ezért ezek a hatások külön korrekciót igényelnek.)
Fontos feltételek és korlátok:
- A Bernoulli-egyenlet általában stacioner (időben állandó) áramlásra vonatkozik.
- Általában ideális, súrlódásmentes (nem viszkózus) közegre és incompressible (szinte változatlan sűrűségű) folyadékra alkalmazható. Nagy sebességű gázáramlásoknál vagy erős sűrűségváltozásnál (kompresszibilis áramlás) korrekciókra van szükség.
- Nem alkalmazható közvetlenül turbulens, erősen veszteséges csőrendszerekre anélkül, hogy az energia veszteségeit (súrlódás, örvények) figyelembe vennénk.
Gyakorlati alkalmazások: a Bernoulli-elvet használják Venturi-mérőkben és Pitot-csövekben (sebességmérés), valamint a repülőgép-szárnyak felemelőerejének magyarázatában — itt a szárny körüli áramlási sebesség-különbségek nyomáskülönbséget hoznak létre, ami felhajtóerőt eredményez. Emellett a csőhálózatok nyomásveszteségeinek, áramlási mintázatok és egyszerű hidraulikai berendezések tervezésénél is gyakran használják.
Összefoglalva: a Bernoulli-elv hasznos és intuitív eszköz az áramló folyadékok és gázok viselkedésének megértéséhez, de alkalmazásakor mindig ellenőrizni kell a feltételeket (stacionaritás, kompresszibilitás, viszkozitás hiánya) és szükség esetén korrigálni a valós veszteségeket vagy nemideális hatásokat.
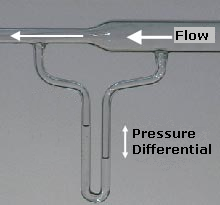
A Bernoulli-elvet bemutató venturi. A jobb oldali víz a nagy csőben lévő nagyobb nyomás miatt alacsonyabb.
Kérdések és válaszok
K: Mi az a Bernoulli-elv?
V: A Bernoulli-elv egy áramlástani fogalom, amely szerint a folyadék sebességének növekedésével csökken a nyomás.
K: Hogyan szemlélteti Bernoulli elvét a jobb oldali kép?
V: A képen látható, hogy a cső széles részében a levegőnek nagyobb a statikus nyomása, mint a vékony részben, ami a folyadék sebességének növekedését okozza a vékony részben.
K: Mi a nyomás?
V: A nyomás egy területre ható erő.
K: Mi történik, ha egy folyadék sebessége megváltozik?
V: A folyadék sebességének változásához a nyomás vagy az erő változásának kell társulnia.
K: Két különböző sebességű áramlásra is érvényes a Bernoulli-elv?
V: Nem, a Bernoulli-elv csak a sebesség és a nyomás változására vonatkozik egyetlen áramlási útvonal mentén.
K: Mit tartalmaz a Bernoulli-elv teljes változata?
V: A Bernoulli-elv teljes változata magában foglalja mind a nyomás, mind a magassági változásokból eredő potenciális energia változásai által végzett munkát.
K: Mit nem vesz figyelembe a Bernoulli-elv?
V: A Bernoulli-elv nem veszi figyelembe a viszkozitást és a tömöríthetőséget.
Keres