Theorema egregium
A Gauss Egregium-tétel (latinul "Figyelemre méltó tétel") a differenciálgeometria egyik legfontosabb eredménye, amelyet Carl Friedrich Gauss bizonyított. A tétel a felületek görbületéről szól. A tétel kimondja, hogy a görbület meghatározható kizárólag szögek, távolságok és ezek mértékének mérésével egy felületen. Nem kell beszélni arról, hogy a felület milyen sajátos módon van beágyazva a környező háromdimenziós euklideszi térbe. Más szóval, egy felület Gauss-görbülete nem változik, ha a felületet meghajlítjuk anélkül, hogy megnyújtanánk.
Gauss így mutatta be a tételt (latinból fordítva):
Ezért az előző cikk képlete önmagában is elvezet a figyelemre méltó tételhez. Ha egy görbült felületet bármilyen más felületre fejlesztünk, a görbület mértéke minden egyes pontban változatlan marad.
A tétel azért "figyelemre méltó", mert a Gauss-görbület kiinduló definíciója közvetlenül felhasználja a felület térbeli helyzetét. Így elég meglepő, hogy az eredmény nem függ a beágyazottságától, minden átélt hajlító és csavaró deformáció ellenére sem.
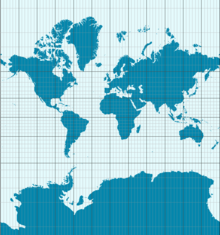
A Theorema Egregium következménye, hogy a Földet nem lehet torzítás nélkül ábrázolni a térképen. Az itt látható Mercator-vetület megőrzi a szögeket, de megváltoztatja a területet. Például az Antarktisz sokkal nagyobbnak látszik, mint amekkora valójában.
Kérdések és válaszok
K: Mi Gauss Theorema Egregium című műve?
V: Gauss Egregium-tétele a differenciálgeometria egyik legfontosabb eredménye, amely a felületek görbületéről szól, és amelyet Carl Friedrich Gauss bizonyított.
K: Hogyan határozható meg a görbület Gauss Egregium-tétele szerint?
V: Gauss Theorema Egregiuma szerint a görbületet kizárólag a szögek, távolságok és ezek mértékének mérésével lehet meghatározni egy felületen.
K: A görbület meghatározásához szükséges-e arról beszélni, hogy a felület milyen sajátos módon van beágyazva a környező háromdimenziós euklideszi térbe?
V: Nem, nem szükséges arról beszélni, hogy a görbület meghatározásához Gauss Egregium-tétele szerint nem szükséges arról beszélni, hogy a felület milyen konkrét módon van beágyazva a környező háromdimenziós euklideszi térbe.
K: Változik-e egy felület gauss-i görbülete, ha a felületet meghajlítjuk anélkül, hogy megnyújtanánk?
V: Nem, egy felület Gauss-féle görbülete nem változik, ha a felületet a Gauss Egregium-tétel szerint nyújtás nélkül meghajlítjuk.
K: Ki mutatta be a tételt ilyen módon?
V: Gauss mutatta be a tételt ilyen módon.
K: Miben figyelemre méltó a tétel?
V: A tétel azért "figyelemre méltó", mert a Gauss-görbület kiinduló definíciója közvetlenül felhasználja a felület térbeli helyzetét. Ezért elég meglepő, hogy az eredmény nem függ a beágyazottságától, minden átélt hajlító és csavaró deformáció ellenére sem.
K: Milyen módon mutatta be Gauss a tételt?
V: Gauss úgy mutatta be a tételt, hogy ha egy görbült felületet bármely más felületre fejlesztünk, akkor a görbület mértéke minden egyes pontban változatlan marad.
Keres